51.N皇后问题

n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

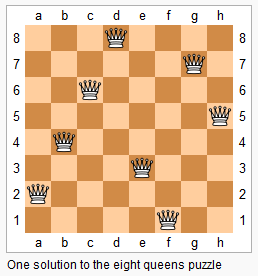
给定一个整数 n，返回所有不同的 n 皇后问题的解决方案。

每一种解法包含一个明确的 n 皇后问题的棋子放置方案，该方案中 'Q' 和 '.' 分别代表了皇后和空位。

示例:

输入: 4
输出: [
 [".Q..",  // 解法 1
  "...Q",
  "Q...",
  "..Q."],
 ["..Q.",  // 解法 2
  "Q...",
  "...Q",
  ".Q.."]
]
解释: 4 皇后问题存在两个不同的解法。

回溯法：

    vector<vector<string>> res;
    void backtrack(vector<string> &cur,int i,int n){
        if(i==n) {
            res.push_back(cur);
            return;
        }
        for(int j=0;j<n;++j){
            if(isValid(cur,i,j)) {
                cur[i][j]='Q';
                backtrack(cur,i+1,n);
                cur[i][j]='.';
            }
        }
    }
    bool isValid(vector<string> &cur,int x,int y){
        for(int i=0;i<x;++i)
            for(int j=0;j<cur[0].size();++j){
                if(cur[i][j]=='Q'&&(y==j||abs(x-i)==abs(y-j))) return false;
            }
        return true;
    }
    vector<vector<string>> solveNQueens(int n) {
        vector<string> cur(n);
        for(int i=0;i<n;++i) cur[0]+='.';
        for(int i=1;i<n;++i) cur[i]=cur[0];
        backtrack(cur,0,n);
        return res;
    }