Noip模拟12 2021.7.12

T1 interval

亏得昨天晚上改掉了T3并且理解了单调栈，今天一扫这题目就知道要用啥了。

先预处理出以a[i]为最大值的最大左右区间。然后再将a[i]取%！！！是的，要不然会影响单调栈的使用。。。

注意一下，这个题的前缀和与a[i]数组都要取%优化，类似《入阵曲》。

可以知道，一个合法的区间应满足。

然后就是昨天T3的类似启发式优化，找到距离较小的区间。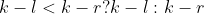

然后枚举那个区间里的每一个位置，都可以算出一个数（以下拿枚举左区间举例）：

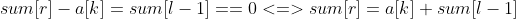
等价右面的柿子就是我们枚举要求的。我们相当于求出一个sum[r]然后通过之前处理出的vector数组去右区间寻找等于sum[r]的数的个数（vector记录每个数（取%以后的）出现的位置）。运用便捷的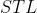——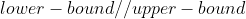即可实现。

最后是有一个小容斥，就是在计算区间时没有讨论l==r的情况，这种情况共n个，ans-n即可。

 1 #include<bits/stdc++.h>
 2 #define int long long
 3 #define write(X) printf("%lld\n",X)
 4 #define Min(A,B) ((A)<(B)?(A):(B))
 5 #define Max(A,B) ((A)>(B)?(A):(B))
 6 using namespace std;
 7 inline int read(){
 8     int x=0,f=1; char ch=getchar();
 9     while(ch<'0'||ch>'9'){ if(ch=='-') f=-1; ch=getchar(); }
10     while(ch>='0'&&ch<='9'){ x=(x<<1)+(x<<3)+(ch^48); ch=getchar(); }
11     return x*f;
12 }
13
14 const int NN=3e6+5000;
15 int n,K,a[NN],sum[NN],ll[NN],rr[NN],ans;
16 stack<int> s,t;
17 vector<int> g[NN];
18 void work(int k,int l,int r){
19     if(k-l<r-k){
20         for(int i=l;i<=k;i++){
21             int tmp=(sum[i-1]+a[k])%K;
22             int ans1=lower_bound(g[tmp].begin(),g[tmp].end(),k)-g[tmp].begin();
23             int ans2=upper_bound(g[tmp].begin(),g[tmp].end(),r)-g[tmp].begin();
24             ans+=ans2-ans1;
25         }
26     }
27     else{
28         for(int i=k;i<=r;i++){
29             int tmp=(sum[i]-a[k]+K)%K;
30             int ans1=lower_bound(g[tmp].begin(),g[tmp].end(),l-1)-g[tmp].begin();
31             int ans2=upper_bound(g[tmp].begin(),g[tmp].end(),k-1)-g[tmp].begin();
32             ans+=ans2-ans1;
33         }
34     }
35 }
36 namespace WSN{
37     inline int main(){
38         n=read(); K=read();
39         g[0].push_back(0);
40         for(int i=1;i<=n;i++){
41             a[i]=read();
42             sum[i]=(a[i]+sum[i-1])%K;
43             g[sum[i]].push_back(i);
44         }
45         for(int i=1;i<=n;i++){
46             while(!s.empty() && a[i]>a[s.top()]) s.pop();
47             if(s.empty()) ll[i]=1;
48             else ll[i]=s.top()+1;
49             s.push(i);
50         }
51         for(int i=n;i;i--){
52             while(!t.empty() && a[i]>=a[t.top()]) t.pop();
53             if(t.empty()) rr[i]=n;
54             else rr[i]=t.top()-1;
55             t.push(i);
56         }
57         for(int i=1;i<=n;i++) a[i]%=K;
58         for(int i=1;i<=n;i++) work(i,ll[i],rr[i]);
59         write(ans-n);
60         return 0;
61     }
62 }
63 signed main(){return WSN::main();}

T2 random

可以推出一个柿子：

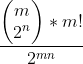
将其化简可以得到：

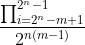
然后我们只需要先用快速幂处理出$$2^n 2^{nm}$$表示分母，然后我们可以发现每1000003个数就有一个1000003的倍数，则如果分子上面累乘的个数大于1000003，那么在累乘过程中应定会出现0，则所有数都是0，分子为0。如果m<1000003就直接暴力求解

然后我们求的是分子和分母的最简形式，考虑约分。

我们发现分母的质因数全是2，那么我们只要找到分子里面质因数分解后有几个2就行。那么怎么找？我们可以将每个2^n减去的那一个数改写为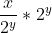形式这样的话如果x中有y个2，其最终结果分式那边一定是个奇数，那么从2^n中提取一个2^y剩下一个偶数减去刚才的奇数得一个奇数，则可以按这种方法一直找到所有2的个数。记得不要忘记用乘法逆元！！

 1 #include<bits/stdc++.h>
 2 #define int long long
 3 #define write(X) printf("%lld ",X)
 4 using namespace std;
 5 inline int read(){
 6     int x=0,f=1; char ch=getchar();
 7     while(ch<'0'||ch>'9'){ if(ch=='-') f=-1; ch=getchar(); }
 8     while(ch>='0'&&ch<='9'){ x=(x<<1)+(x<<3)+(ch^48); ch=getchar(); }
 9     return x*f;
10 }
11
12 const int mod=1e6+3;
13 int n,m,a,b,c,d,ans1,ans2;
14 inline int qmo(int a,int b){
15     int ans=1,c=mod; a%=c;
16     while(b){
17         if(b&1) ans=(ans*a)%c;
18         a=(a*a)%c;
19         b>>=1;
20     } return ans;
21 }
22 namespace WSN{
23     inline int main(){
24         n=read();m=read();
25         d=a=qmo(2,n%(mod-1));
26         b=qmo(a,m%(mod-1));
27         int inv2=500002,num2=n;
28         for(int i=1;i<m;i++){
29             d=d*(a-i)%mod;
30             if(!d) break;
31         }
32         for(int i=1;(1ll<<i)<=m-1;i++){
33             num2+=(m-1)/(1ll<<i);
34         }
35         c=qmo(inv2,num2);
36         d=d*c%mod;
37         b=b*c%mod;
38         ans1=(b-d+mod)%mod;
39         ans2=b%mod;
40         write(ans1); write(ans2);
41         return 0;
42     }
43 }
44 signed main(){return WSN::main();}

T3 seq

这题上来一看，我去，根本想不到用什么方面的知识。结果，还真不用什么知识，就是个模拟（但就是不会。。。）。

记录一个up，down分别表示最优及最劣情况，每个开一个pair（x，y）表示那一位数的值，以及使用那个数的个数。

然后正向预处理出本应得到的最优，及最劣情况。

具体为如果连续使用了两个同一个数，up就换成新的大数;同理如果大于5个，down的数就更新。

如果遇到有数的空格就进行比较，保证up最优，down最劣即可。

经过小小的思考就可以加上判断不成立的条件。

然后建造一个bin[]桶函数，按照最劣情况填数，如果桶的一个较大值满，则换成小一号的数继续装。

 1 #include<bits/stdc++.h>
 2 #define val first
 3 #define num second
 4 #define int long long
 5 #define write(X) printf("%lld\n",X)
 6 using namespace std;
 7 inline int read(){
 8     int x=0,f=1; char ch=getchar();
 9     while(ch<'0'||ch>'9'){ if(ch=='-') f=-1; ch=getchar(); }
10     while(ch>='0'&&ch<='9'){ x=(x<<1)+(x<<3)+(ch^48); ch=getchar(); }
11     return x*f;
12 }
13 const int NN=2e5+500,mod=1e6+3;
14 int n,a[NN],bin[NN];
15 pair<int,int> up[NN],down[NN];
16 namespace WSN{
17     inline int main(){
18         n=read();
19         for(int i=1;i<=n;i++) a[i]=read();
20         if(a[1]!=1 && a[1]!=0) {printf("-1\n\n");return 0;}
21         up[1]=make_pair(1,1); down[1]=make_pair(1,1);
22         for(int i=2;i<=n;i++){
23             up[i]=up[i-1]; down[i]=down[i-1];
24             up[i].num++; down[i].num++;
25             if(up[i].num>2) up[i].val++,up[i].num=1;
26             if(down[i].num>5) down[i].val++,down[i].num=1;
27             if(!a[i]) continue;
28             if(up[i].val>a[i]) up[i]=make_pair(a[i],2ll);
29             if(down[i].val<a[i]) down[i]=make_pair(a[i],1);
30             if(down[i].val>a[i] || up[i].val<a[i]) {printf("-1\n\n");return 0;}
31         }
32         for(int i=1;i<=n;i++){
33         }
34         if(up[n].num==1) up[n].val--,up[n].num=up[n-1].num+1;
35         if(up[n].val<down[n].val) {printf("-1\n\n");return 0;}
36         a[n]=up[n].val; write(a[n]);
37         bin[a[n]]=1;
38         for(int i=n-1;i>=1;i--){
39             if(!a[i]){
40                 int v=min(a[i+1],up[i].val);
41                 if(bin[v]==5) v--;
42                 a[i]=v;
43             }
44             bin[a[i]]++;
45         }
46         for(int i=1;i<=n;i++)
47             printf("%lld ",a[i]);
48         return 0;
49     }
50 }
51 signed main(){return WSN::main();}

END

---

这次考试并未得到自己想要的分数，T1非常可惜，自己想的复杂度是n^2或者nlogn结果出来跟打线段数暴力分一样，哭死好吧，早知道二十分钟线段树把这题干掉直接去打T3了。。。。结果T2，T3都比较蒙敲了暴力水了20分就结束了，可恶。。。。