【BZOJ3545】Peaks(Kruskal重构树 主席树)

题目链接

大意

给出有\(N\)个点\(M\)条边的一张图，其中每个点都有一个High值，每条边都有一个Hard值。

再给出\(Q\)个询问：\(v\) \(x\) \(k\)

每次询问查询从点\(v\)出发，只经过Hard值小于等于\(x\)的边能到达的点中，第\(k\)大的High值。

思路

考虑Kruskal重构树：

在Kruskal算法求最小生成树的时候，每次加边将该边化成一个点，该点的点权值是原边权值。

然后用该点与两个连通块连边。

如图：



变为：



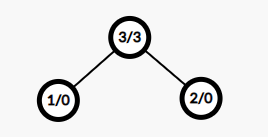
（左侧为点编号，右侧为点权）

这样重建一颗树后，可以发现其是一个大根堆。（根权最大）

然后我们就可以用倍增的思想在\(O(log(N))\)的时间内求出对于一对\((v,x)\)的上界。

（小注：上界指以该上界为根的子树内的点都可以被这对\((v,x)\)访问到）

在用Kruskal重构后，我们就可以将该问题变为求一颗子树内第\(K\)大的点权值。

对于这个问题，我们可以用主席树维护前缀的权值线段树，查询一颗子树时用DFN序就行了。

代码

附上一篇很慢的代码

#include<map>
#include<cstdio>
#include<vector>
#include<algorithm>
using namespace std;
const int MAXK=25;
const int MAXN=200005;
const int MAXM=500005;
int N,M,Q,Cnt,NCnt,PCnt,Root[MAXN];
int A[MAXN],Fa[MAXN],Val[MAXN];
int Dfn[MAXN],Tid[MAXN],Siz[MAXN];
int fa[MAXN][MAXK],Vat[MAXN][MAXK];
struct Edge{int x,y,z;}s[MAXM];
struct Quer{int p,x,k;}q[MAXM];
struct Node{int num,ch[2],l,r;}t[MAXM*120];
bool cmp(Edge X,Edge Y){return X.z<Y.z;}
int Find(int x){return Fa[x]==x?x:Fa[x]=Find(Fa[x]);}
int Len,B[MAXN],E[MAXN],ValCnt;
vector<int>P[MAXN];
map<int,int>Mp;
void Val_Init(){
	sort(B+1,B+Len+1);B[0]=-1;
	for(int i=1;i<=Len;i++)
		if(B[i]!=B[i-1]){
			Mp[B[i]]=++ValCnt;
			E[ValCnt]=B[i];
		}
	for(int i=1;i<=Cnt;i++)A[i]=Mp[A[i]];
}
void DFS(int u){
	Dfn[u]=++NCnt;
	Tid[NCnt]=u;Siz[u]=1;
	int size=P[u].size();
	for(int i=0;i<size;i++){
		int v=P[u][i];
		fa[v][0]=u;DFS(v);
		Vat[v][0]=max(Val[v],Val[u]);
		Siz[u]+=Siz[v];
	}
}
void Build(int &rt,int l,int r){
	rt=++PCnt;
	t[rt].l=l;t[rt].r=r;
	if(l==r)return ;
	int mid=(l+r)/2;
	Build(t[rt].ch[0],l,mid);
	Build(t[rt].ch[1],mid+1,r);
}
void Insert(int &rt,int ort,int p,int val){
	rt=++PCnt;t[rt]=t[ort];t[rt].num++;
	if(t[rt].l==t[rt].r)return ;
	int mid=(t[rt].l+t[rt].r)>>1;
	if(p<=mid)Insert(t[rt].ch[0],t[ort].ch[0],p,val);
	else Insert(t[rt].ch[1],t[ort].ch[1],p,val);
}
int Find(int rt1,int rt2,int k){
	if(t[rt1].l==t[rt1].r)return t[rt1].l;
	int num=t[t[rt1].ch[0]].num-t[t[rt2].ch[0]].num;
	if(num>=k)return Find(t[rt1].ch[0],t[rt2].ch[0],k);
	return Find(t[rt1].ch[1],t[rt2].ch[1],k-num);
}
int Get(int p,int x){
	for(int i=20;i>=0;i--)
		if(Vat[p][i]<=x&&fa[p][i])
			p=fa[p][i];
	return p;
}
void Init(){
	sort(s+1,s+M+1,cmp);Cnt=N;
	for(int i=1;i<=M;i++){
		int x=Find(s[i].x);
		int y=Find(s[i].y);
		if(x==y)continue;
		Fa[x]=++Cnt;Fa[y]=Cnt;
		Val[Cnt]=s[i].z;
		P[Cnt].push_back(x);
		P[Cnt].push_back(y);
	}
	Val_Init();
	for(int i=1;i<=Cnt;i++)
		if(Fa[i]==i)DFS(i);
	for(int k=1;k<=20;k++)
		for(int i=1;i<=Cnt;i++){
			fa[i][k]=fa[fa[i][k-1]][k-1];
			Vat[i][k]=max(Vat[i][k-1],Vat[fa[i][k-1]][k-1]);
		}
	PCnt=-1;
	Build(Root[0],1,ValCnt);
	for(int i=1;i<=Cnt;i++){
		if(A[Tid[i]]==1){
			Root[i]=Root[i-1];
			continue;
		}
		Insert(Root[i],Root[i-1],A[Tid[i]],1);
	}
}
int main(){
	scanf("%d%d%d",&N,&M,&Q);
	for(int i=1;i<=N;i++)
		scanf("%d",&A[i]),B[++Len]=A[i];B[++Len]=0;
	for(int i=1;i<=2*N;i++)Fa[i]=i;
	for(int i=1;i<=M;i++)
		scanf("%d%d%d",&s[i].x,&s[i].y,&s[i].z);
	for(int i=1;i<=Q;i++)
		scanf("%d%d%d",&q[i].p,&q[i].x,&q[i].k);
	Init();
	for(int i=1;i<=Q;i++){
		int Tp=Get(q[i].p,q[i].x);
		int rt1=Root[Dfn[Tp]+Siz[Tp]-1],rt2=Root[Dfn[Tp]-1];
		int num=t[rt1].num-t[rt2].num;
		if(num<q[i].k){
			printf("-1\n");
			continue;
		}
		int ret=Find(rt1,rt2,num-q[i].k+1);
		printf("%d\n",E[ret]);
	}
}