NOAA OneStop

https://data.noaa.gov/onestop/about

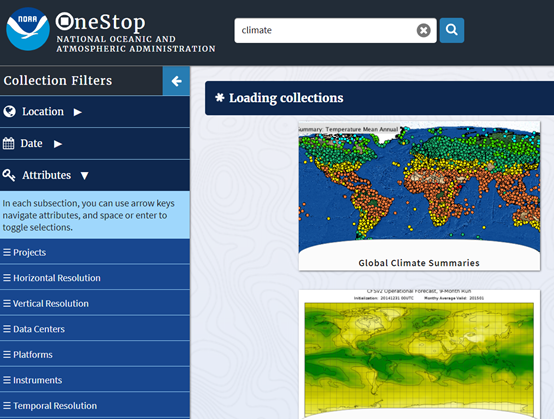
NOAA 数据搜索平台，在一个地方同时搜索NOAA的 Geophysical, oceans, coastal, weather and climate 数据，相当于一个摘要数据集，搜索结果提供数据相关信息链接。典型的数据搜索界面，简单摸索即可使用。

NCDC & NCEI

https://www.ncdc.noaa.gov https://www.ncei.noaa.gov

NOAA的数据中心 用于下载气象数据。

点击Data Access来到数据界面。

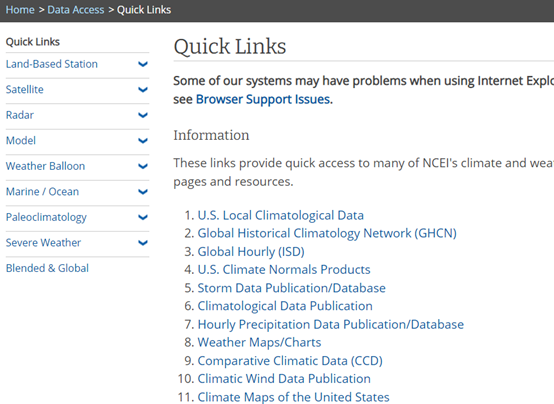
可以在这里搜索需要的数据集，然后去下述网址下载

https://www.ncei.noaa.gov/access/search/dataset-search

通过筛选位置，日期，数据集，获得自己想要的数据。

NOAA数据下载方法的更多相关文章

  1. 腾讯QQ群数据下载方法（7000万个qq群资料全泄漏）

    仔细读完一定能找到自己需要的东西 据新华网报道,国内知名安全漏洞监测平台乌云20日公布报告称,腾讯QQ群关系数据被泄露,网上可以轻易就能找到数据下载链接,根据这些数据,通过QQ号可以查询到备注姓名.年 ...

  2. Landsat数据下载方法小结

    本文转载自:http://malagis.com/landsat-data-download.html 本文介绍下载Landsat数据的方法. Landsat(美国陆地卫星)是遥感应用中常用的卫星数据 ...

  3. hadoop ncdc数据下载方法

    我在看<Hadoop权威指南>时,里面提供了NCDC天气数据样本,提供的下载链接是:点击打开链接,但是里面只提供了1901和1902这两年的数据,这未免也太少了点!完全称不上“BIG DA ...

  4. SMOS数据产品介绍与下载方法

    1. SMOS数据介绍 The Soil Moisture and Ocean Salinity (SMOS) 卫星是欧空局发射的一颗以探测地球土壤水含量以及海表盐度为目标的卫星,卫星所搭载的唯一载荷 ...

  5. MODIS系列之NDVI（MOD13Q1）一：数据下载(一)基于插件

    引言: 写MODIS数据处理这个系列文章的初衷,主要是为了分享本人处理MODIS数据方面的一些经验.鉴于网上对这方面系统性的总结还比较少,我搜集资料时也是走了许多的弯路,因此希望通过此文让初学者能够更 ...

  6. SMAP数据产品介绍与下载方法

    1 SMAP(Soil Moisture Active and Passive)数据介绍 SMAP baseline science data products在下面的表格中展示,这些数据产品可以从两 ...

  7. EB-SAM9G45裸机程序下载方法

    开发板:EB-SAM9G45 这里提供一种裸程序下载的方法. 在官方提供的下载方法中有手动下载和自动下载,它们都离不开SAM-BA软件,而该软件使用比较麻烦,而且操作不当很容易导致电脑蓝屏,还有一个很 ...

  8. STM32下载方法

    一.JLINK下载方法 1.硬件设置 Boot0,Boot1 = 0,*(测试通过) Boot0,Boot1 = 1,0或者0,1(未测试) 2.软件设置 MDK设置 ① 选择Project -> ...

  9. ios 网络数据下载和JSON解析

    ios 网络数据下载和JSON解析 简介 在本文中笔者将要给大家介绍ios中如何利用NSURLConnection从网络上下载数据,如何解析下载下来的JSON数据格式,以及如何显示数据和图片的异步下载 ...

随机推荐

  1. [atARC088F]Christmas Tree

    合并具有交换律,因此即将一个连通块(初始为空)与一条链合并(其中各选1点,初始直接替换) 把插入改为染色,等价于对树上的一条链(包括点和边)染色,其中恰好有1个已经被染色的点(初始任意) 对于&quo ...

  2. [bzoj1089]严格n元树

    设f[i]表示深度不超过i的方案数,那么有f[0]=1,$f[i]=f[i-1]^{n}+1$,然后用高精度即可(注意深度恰好为d还要用f[d]-f[d-1]才是答案) 1 #include<b ...

  3. [loj3313]序列

    定义$C_{i}$表示令$i,i+1,i+2,...$的位置减1的操作,定义$I_{i}$表示令$i,i+2,i+4,...$的位置减1的操作 结论1:一定存在一种最优解使得$\forall i$不同 ...

  4. [bzoj2245]工作安排

    由于价格是单调递增的,因此可以直接建立Si条边,流量和价格依次为给定的函数即可(如果价格不递增,可以考虑动态加边等操作) 1 #include<bits/stdc++.h> 2 using ...

  5. python的基础知识-冷门

    可变与不可变: 大部分python对象是可变的,e.g列表,字典,自定义的类. 字符串和元祖是不可变的. pass用于占位符,py不允许有空代码块 range和xrange 生成整数列表 xrange ...

  6. Linux 进程与线程

    进程与线程   进程 进程就是在操作系统中运行的程序,是操作系统资源管理的最小单位.一个进程可以管理多个线程,线程相对轻量,可以共享进程地址空间 线程来源 一个进行在运行的过程中,不可能一直占据着CP ...

  7. 腾讯云联合中国信通院&作业帮等首发《降本之源-云原生成本管理白皮书》

    在11月4日举办的2021腾讯数字生态大会云原生专场上,腾讯云联合中国信通院.作业帮等率先在国内重磅发布了<降本之源-云原生成本管理白皮书>(简称白皮书),基于腾讯云在业内最大规模的 Ku ...

  8. 数据库之JDBC

    1.简单认识一下JDBC 1).JDBC是什么? java database connection       java数据库连接 作用:就是为了java连接mysql数据库嘛 要详细的,就面向百度编 ...

  9. 【每天五分钟大数据-第一期】 伪分布式+Hadoopstreaming

    说在前面 之前一段时间想着把 LeetCode 每个专题完结之后,就开始着手大数据和算法的内容. 想来想去,还是应该穿插着一起做起来. 毕竟,如果只写一类的话,如果遇到其他方面,一定会遗漏一些重要的点 ...

  10. Android Https相关完全解析

    转载: 转载请标明出处: http://blog.csdn.net/lmj623565791/article/details/48129405: 本文出自:[张鸿洋的博客] 一.概述 其实这篇文章理论 ...