矩阵n次幂的计算
1、归纳法
题目一
2、递推关系
题目一
题目二
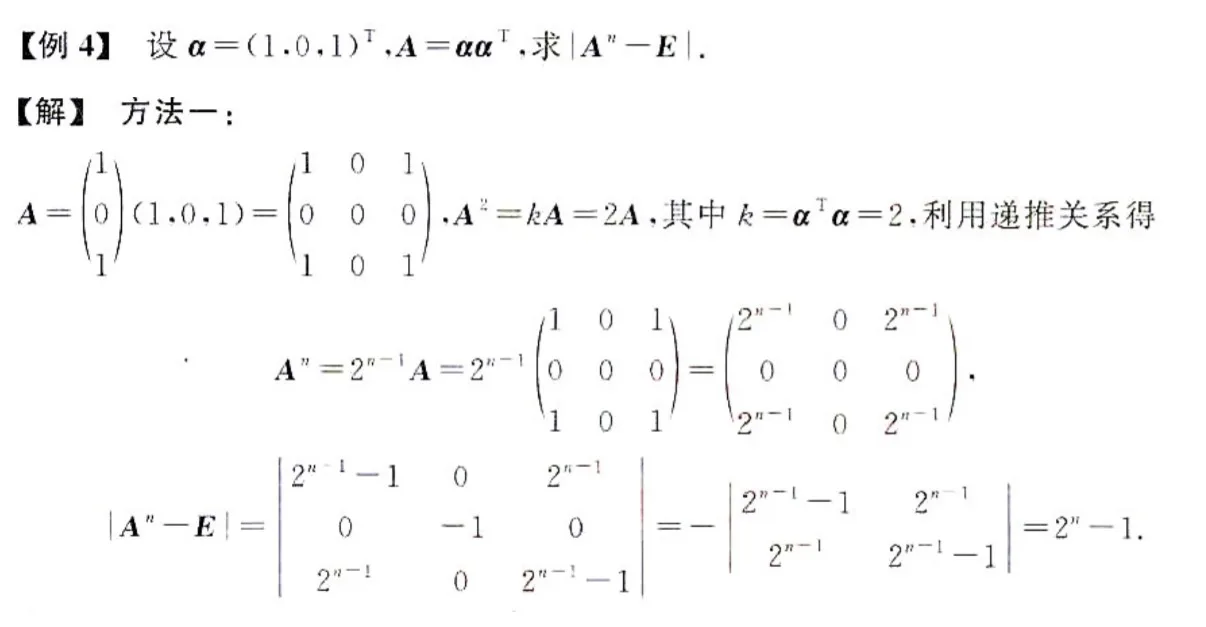
3、方阵
题目一
4、矩阵对角化（重点）
题目一
题目二
题目三
题目四
5、矩阵性质（综合）
题目一
题目二
对于副对角线：
题目三
矩阵n次幂的计算的更多相关文章
- ACM学习历程—HDU5667 Sequence（数论 && 矩阵乘法 && 快速幂）
http://acm.hdu.edu.cn/showproblem.php?pid=5667 这题的关键是处理指数,因为最后结果是a^t这种的,主要是如何计算t. 发现t是一个递推式,t(n) = c ...
- Luogu 1349 广义斐波那契数列（递推，矩阵，快速幂）
Luogu 1349 广义斐波那契数列(递推,矩阵,快速幂) Description 广义的斐波那契数列是指形如\[A_n=p*a_{n-1}+q*a_{n-2}\]的数列.今给定数列的两系数p和q, ...
- 洛谷 P4910 帕秋莉的手环 矩阵乘法+快速幂详解
矩阵快速幂解法: 这是一个类似斐波那契数列的矩乘快速幂,所以推荐大家先做一下下列题目:(会了,差不多就是多倍经验题了) 注:如果你不会矩阵乘法,可以了解一下P3390的题解 P1939 [模板]矩阵加 ...
- Qbxt 模拟赛 Day4 T2 gcd(矩阵乘法快速幂)
/* 矩阵乘法+快速幂. 一开始迷之题意.. 这个gcd有个规律. a b b c=a*x+b(x为常数). 然后要使b+c最小的话. 那x就等于1咯. 那么问题转化为求 a b b a+b 就是斐波 ...
- 矩阵乘法快速幂 codevs 1574 广义斐波那契数列
codevs 1574 广义斐波那契数列 时间限制: 1 s 空间限制: 256000 KB 题目等级 : 钻石 Diamond 题目描述 Description 广义的斐波那契数列是指形如 ...
- poj3070--Fibonacci(矩阵的高速幂)
Fibonacci Time Limit: 1000MS Memory Limit: 65536K Total Submissions: 9650 Accepted: 6856 Descrip ...
- 矩阵二分快速幂优化dp动态规划
矩阵快速幂代码: int n; // 所有矩阵都是 n * n 的矩阵 struct matrix { int a[100][100]; }; matrix matrix_mul(matrix A, ...
- 【bzoj3231】[Sdoi2008]递归数列 矩阵乘法+快速幂
题目描述 一个由自然数组成的数列按下式定义: 对于i <= k:ai = bi 对于i > k: ai = c1ai-1 + c2ai-2 + ... + ckai-k 其中bj和 cj ...
- C++-POJ3735-Training little cats[矩阵乘法][快速幂]
矩阵快速幂,主要是考构造.另外,swap总是写龊? 为什么?干脆放弃了.唉,我太难了. 思路:操作e和s都很好想,主要是g操作 我们可以额外空出一位,记为1,每次要加1,就对这个额外的1进行计算即可 ...
随机推荐
- Spring5（七）——AOP注解
一.AOP注解 1.介绍 上一节介绍了 AspectJ 框架如何实现 AOP,具体的实现方式是通过 xml 来进行配置的.xml 方式思路清晰,便于理解,但是书写过于麻烦.这一节介绍注解的方式来进行 ...
- 聊一聊开闭原则(OCP).
目录 简述 最早提出(梅耶开闭原则) 重新定义(多态开闭原则) 深入探讨 OCP的两个特点 对外扩展开放(Open for extension) 对内修改关闭 抽象 关闭修改.对外扩展? 简述 在面向 ...
- promise入门基本使用
Promise入门详解和基本用法 异步调用 异步 JavaScript的执行环境是单线程. 所谓单线程,是指JS引擎中负责解释和执行JavaScript代码的线程只有一个,也就是一次只能完成一项任 ...
- 安装 MongoDb
下面具体说下MongoDB安装之后的一些配置操作 [声明]我的安装路径是:C:\Program Files\MongoDB\Server\3.4 1. 创建数据库路径(data目录).日志路径(log ...
- django class类即视图类添加装饰器的几种方法
根据别人发布整理,个人爱好收集(原文:https://blog.csdn.net/mydistance/article/details/83958655 ) 第一种:定义函数装饰器,在函数,类中使用函 ...
- 定要过python二级 第11套
1. 2.乃至好的代码片段与解决方法,我保存在了 H:盘中python中的:H:\python\python二级好的代码片段与错误解决 3.接着第一个点,为什么print(read(f)) 把f 放 ...
- P1712-[NOI2016]区间【线段树,尺取法】
正题 题目链接:https://www.luogu.com.cn/problem/P1712 题目大意 \(n\)个区间,求出其中\(m\)个区间使得它们有覆盖同一个点且最长区间长度减去最短长度最小. ...
- P5956-[POI2017]Podzielno【数学】
正题 题目链接:https://www.luogu.com.cn/problem/P5956 题目大意 \(B\)进制下,给出序列\(a\),\(a_i\)表示数字\(i\)有多少个.求一个最大的\( ...
- SpringBoot 添加本地 jar 文件
前言 有时候我们在项目中,会用到一些本地 jar 包文件,比如隔壁公司自己打包的: 此时无法从maven远程仓库拉取: 那么我们可以考虑把 jar 文件安装到本地 maven 库中,然后再添加依赖. ...
- Ubuntu-mate-20.04-desktop安装总结
ubuntu-mate-20.04-desktop效果先展示下: Ubuntu用MATE桌面环境同时配合compiz 窗口管理器是目前为止得到的桌面中最喜欢的样式 一.ubuntu-mate官网下载i ...