【LeetCode】1631. 最小体力消耗路径 Path With Minimum Effort

• 作者： 负雪明烛
• id： fuxuemingzhu
• 个人博客：http://fuxuemingzhu.cn/

---

目录

• 题目描述
• 解题思路
• • 并查集
• 代码
• 刷题心得
• 欢迎加入组织
• 日期

题目地址：https://leetcode-cn.com/problems/path-with-minimum-effort/

题目描述

你准备参加一场远足活动。给你一个二维 rows x columns 的地图 heights ，其中 heights[row][col] 表示格子 (row, col) 的高度。一开始你在最左上角的格子 (0, 0) ，且你希望去最右下角的格子 (rows-1, columns-1) （注意下标从 0 开始编号）。你每次可以往 上，下，左，右 四个方向之一移动，你想要找到耗费 体力 最小的一条路径。

一条路径耗费的 体力值 是路径上相邻格子之间 高度差绝对值 的 最大值 决定的。

请你返回从左上角走到右下角的最小 体力消耗值 。

示例 1：

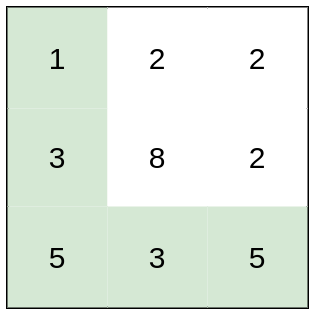
输入：heights = [[1,2,2],[3,8,2],[5,3,5]]
输出：2
解释：路径 [1,3,5,3,5] 连续格子的差值绝对值最大为 2 。
这条路径比路径 [1,2,2,2,5] 更优，因为另一条路径差值最大值为 3 。

示例 2：

输入：heights = [[1,2,3],[3,8,4],[5,3,5]]
输出：1
解释：路径 [1,2,3,4,5] 的相邻格子差值绝对值最大为 1 ，比路径 [1,3,5,3,5] 更优。

示例 3：

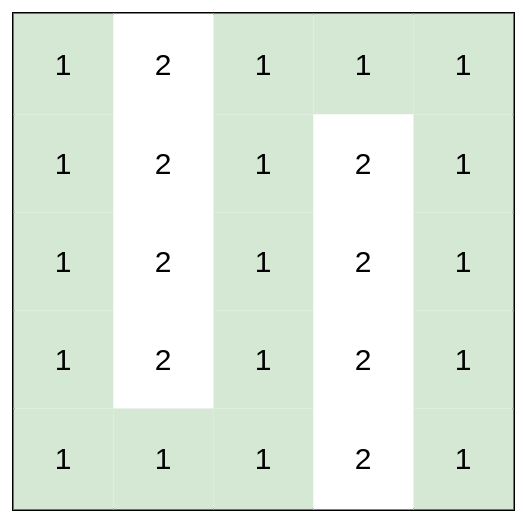
输入：heights = [[1,2,1,1,1],[1,2,1,2,1],[1,2,1,2,1],[1,2,1,2,1],[1,1,1,2,1]]
输出：0
解释：上图所示路径不需要消耗任何体力。

提示：

1. rows == heights.length
2. columns == heights[i].length
3. 1 <= rows, columns <= 100
4. 1 <= heights[i][j] <= 106

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/path-with-minimum-effort
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

解题思路

并查集

拿到这个题时，大家的第一思路是不是**动态规划（DP）**呢？这个题和第 62 题『不同路径』很像，62 题是机器人从左上角走到右下角有多少不同的走法。

两个题目最大的不同点在于，第 62 题限制了机器人每次只能向下或者向右移动一步。因此，到达每个格子的状态只与其左边和上边的格子状态有关，而左边和上边的格子的状态我们都已经在之前计算过。因此第 62 题可以用 DP 求解。

本题中，如果我们定义每个格子的状态是到达该格子的最小体力消耗路径，那么每个格子的状态其实跟上下左右四个方向都有关。如果我们仍然按照从左到右，从上到下的两重 for 循环已经无法搞定 4 个方向，因此只能放弃 DP 方法。

那这个题在考察什么呢？重要的提示就在于 4 个方向！一个格子和周围 4 个方向相邻格子的状态都有关，这就是在考察图！（如果题目说的是 8 个方向，那么更明显）。

我们把每个格子当做图的一个节点，把相邻两个格子的高度差绝对值当做边的权重。就可以把输入的矩阵转化成为每条边都带有权重的图。上文中的示例给出的矩阵可以转成下面的图，可以看到从最左上角到最右下角的最小体力消耗路径为紫色所示的路径，最小体力消耗值是该路径中的边的最大权重，即为 2。

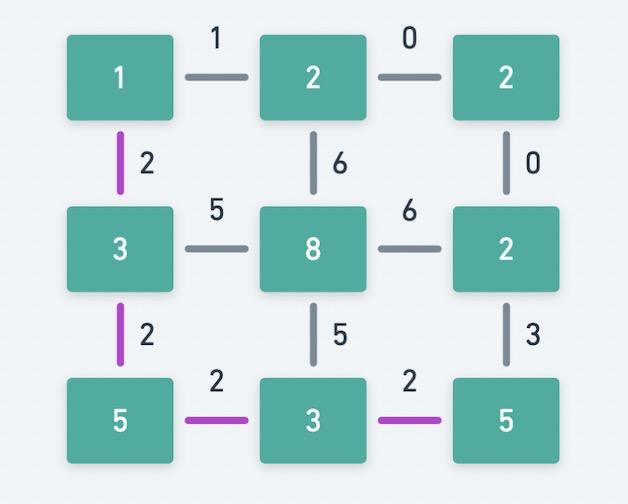
当把题目转成图的问题之后，怎么求解最小体力消耗路径呢？每日一题已经出了这么久的并查集，今天的题目也不会让我们失望。对，我们认为这是在求从最左上角的节点到最右下角的节点的连通性问题。具体来说，我们可以先把图中的所有边都去掉，然后按照边的权重大小，把边再逐个的添加上。当我们添加到某一条边时，最左上角的节点和最右下角的节点连通了，那么该边的权重就是我们要求的最小体力消耗值。

下面举例说明，以上面的图为例。

1. 最开始，移除所有边。
   
2. 然后添加上权重最小的边，即权重为 0 的边。此时的物理含义是判断 0 是不是最小体力消耗值，发现最左上角和最右下角未连通，需要继续。
   
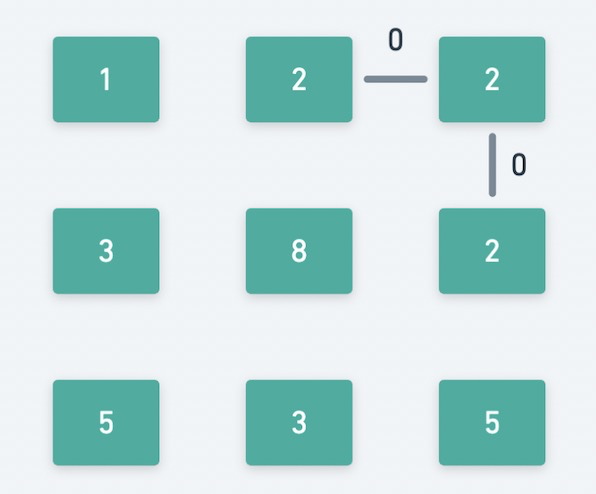
3. 然后添加上权重第 2 小的边，即权重为 1 的边。此时的物理含义是判断 1 是不是最小体力消耗值，发现最左上角和最右下角未连通，需要继续。
   
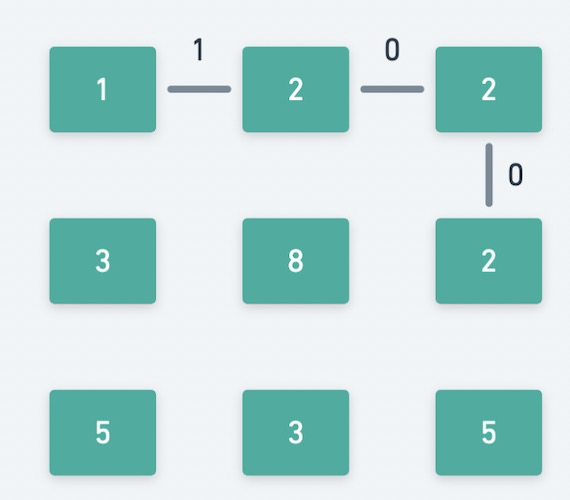
4. 然后添加上权重第 3 小的边，即权重为 2 的边。此时的物理含义是判断 2 是不是最小体力消耗值，发现最左上角和最右下角已经连通，找到答案。
   

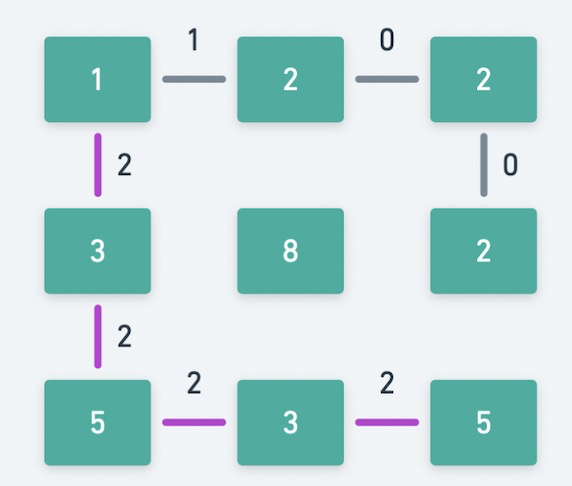
本题中并查集的作用就是判断最左上角和最右下角是否连通，以及当每次添加上一条新的边时，若该边属于两个未联通的区域，则把两个区域连通起来。

代码

在分析完解题思路之后，代码就不难了。

1. 首先需要一个并查集的数据结构 DSU，这里直接使用模板。
2. 然后我们需要生成所有的边，并保存到 edges 中。edges[i] 是个 [边的权重，边的第一个顶点，边的第二个顶点] 三元组。把边的权重放在第一位的原因是，我们需要对边的权重排序，在 Python 中调用sort()函数，默认会根据第一个元素排。
3. 按照权重对所有的边进行排序sort()。
4. 遍历所有边，连通这个边的两个节点。并且判断，如果最左上角和最右下角两个节点是否连通了。如果已经连通，则此时的边的权重就是我们要求的最小体力消耗值。

代码中的一个技巧就是把二维左边转成了一维，即第 i 行第 j 列映射成了 i * N + j。因为实现并查集时使用的数组结构，因此需要把每个节点的二维坐标映射成该数组中的具体位置。这是一个在解决数组问题中的技巧。

另外，需要注意，在两重 for 循环中我们把每个顶点和右边、下边相邻的两个边放到了 edges 中。这样能保证所有的边都不重复不遗漏地放到 edges 里。此时也要注意数组越界，因为最右边的那一列节点没有更右边的边了，最下边的那一行也没有更下边的边了。

Python2 的代码如下，其他语言可以修改得到。

class Solution(object):
    def minimumEffortPath(self, heights):
        """
        :type heights: List[List[int]]
        :rtype: int
        """
        M = len(heights)
        N = len(heights[0])
        dsu = DSU()
        edges = []
        for i in range(M):
            for j in range(N):
                pos = i * N + j
                if i < M - 1:
                    edges.append([abs(heights[i + 1][j] - heights[i][j]), pos, pos + N])
                if j < N - 1:
                    edges.append([abs(heights[i][j + 1] - heights[i][j]), pos, pos + 1])
        edges.sort()
        for edge in edges:
            dsu.union(edge[1], edge[2])
            if dsu.connected(0, M * N - 1):
                return edge[0]
        return 0

class DSU:
    def __init__(self):
        self.par = range(10001)

    def find(self, x):
        if x != self.par[x]:
            self.par[x] = self.find(self.par[x])
        return self.par[x]

    def union(self, x, y):
        self.par[self.find(x)] = self.find(y)

    def connected(self, x, y):
        return self.find(x) == self.find(y)

刷题心得

这种题需要有一定的抽象能力，当抽象完成之后得到图、知道用并查集求解之后，代码并没有那么难。

如果一个题拿到了之后，思考了 10 分钟还没有任何思路的话，就勇敢地去看别人的题解吧！相信我，在刷题的过程中避免一直想一直想。「空想」不会给你带来新的收获，真正的进步应该是学习来的，不是「空想」来的！而且想了半天没想出来，既浪费时间，又打击自信心！

我就是一路看别人的题解走过来的，理解了别人的题解之后，靠自己的理解记忆，默写一遍代码，如果出错，再分析为什么出错，和原来的题解代码有什么不同。越到后面就熟练，我相信你一定会进步很大的。

本题中的并查集，模板是通用的，但是建议理解之后每次都默写，不要一直 copy。

OK，这就是本次题解的全部内容了，如果你觉得我的题解对你有帮助的话，求赞、求关注、求转发、求收藏。你的认可就是我前进的最大动力！我们明天再见！

欢迎加入组织

算法每日一题是个互相帮助、互相监督的力扣打卡网站，其地址是 https://www.ojeveryday.com/

想加入千人刷题群的朋友，可以复制上面的链接到浏览器，然后在左侧点击“加入组织”，提交力扣个人主页，即可进入刷题群。期待你早日加入。

欢迎关注我的公众号：每日算法题

日期

2021 年 1 月 28 日 —— 日更公众号的第5天，加油！