多个n维向量围成的n维体积的大小

前言

上周我们数学老师给了我们一道题，大意就是两个向量a和b，一个点M=$x*a+y*b$，x,y有范围，然后所有M组成的面积是一个定值，求x+y的最小值。当然这是道小水题，但我在想，如果把两个向量变成多个向量，二维变成高维的话，那会怎么样呢。

分析

众所周知，两个二维向量可围成平行四边形。如果再多一个就相当于将该平行四边形沿该向量平移，如下图，总面积就相当于如图蓝色框出的面积（即平移时扫过的体积）。

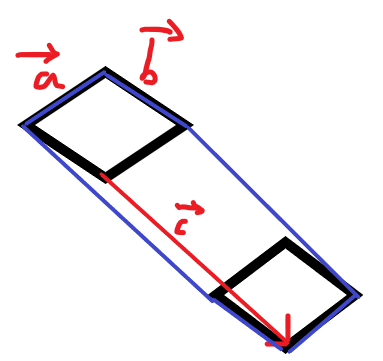
它可以分解成下图三个平行四边形

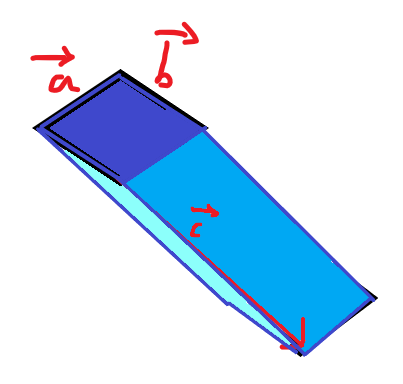
所以$S=a \times b +a \times c +b \times c$(注意这里为了方便向量不标箭头)

如果再加一个向量，就相当于将该图形整体平移

易得：对于m个二维向量，围成的面积

$$S=\sum_{a,b是1到m的一个组合} a \times b$$

进一步，将二维扩展为三维，对于三个三维向量围成的平行四边形体，此时再加一个向量，就相当于将该几何体平移，求整个几何体扫过的体积。

经过我画图验证可得总体积

$$V=\sum_{a,b,c是1到m的一个组合} (a \times b) \cdot c$$

更进一步，扩展到n维，此时它的体积（我也不知道高维下的空间大小叫什么，就先沿用体积好了）就难以用点积和叉积表示了，我们用$f(a_1,a_2,...,a_n)$表示n个n维向量围成的体积，则：

$$V=\sum_{i,j,k,...是1到m的一个组合} f(a_i,a_j,a_k,...)$$

$f(a_i)$可以用行列式来求解，即：

设m个n维向量分别表示为$v_i=(a_{i,1},...,a_{i,n})$

$f(a_1,a_2,...,a_n)=$

\left[

\begin{array}{cccc}
a_{1,1}  & ... & a_{1,n} \\
...  & ...   & ...\\
a_{n,1}  & ... & a_{n,n}
\end{array}

\right]

如此一来，我们就得到了多个n维向量围成的n维体积的大小的计算公式