看动画学算法之:平衡二叉搜索树AVL Tree

目录

• 简介
• AVL的特性
• AVL的构建
• AVL的搜索
• AVL的插入
• AVL的删除

简介

平衡二叉搜索树是一种特殊的二叉搜索树。为什么会有平衡二叉搜索树呢？

考虑一下二叉搜索树的特殊情况，如果一个二叉搜索树所有的节点都是右节点，那么这个二叉搜索树将会退化成为链表。从而导致搜索的时间复杂度变为O(n),其中n是二叉搜索树的节点个数。

而平衡二叉搜索树正是为了解决这个问题而产生的，它通过限制树的高度，从而将时间复杂度降低为O(logn)。

AVL的特性

在讨论AVL的特性之前，我们先介绍一个概念叫做平衡因子，平衡因子表示的是左子树和右子树的高度差。

如果平衡因子=0，表示这是一个完全平衡二叉树。

如果平衡因子=1，那么这棵树就是平衡二叉树AVL。

也就是是说AVL的平衡因子不能够大于1。

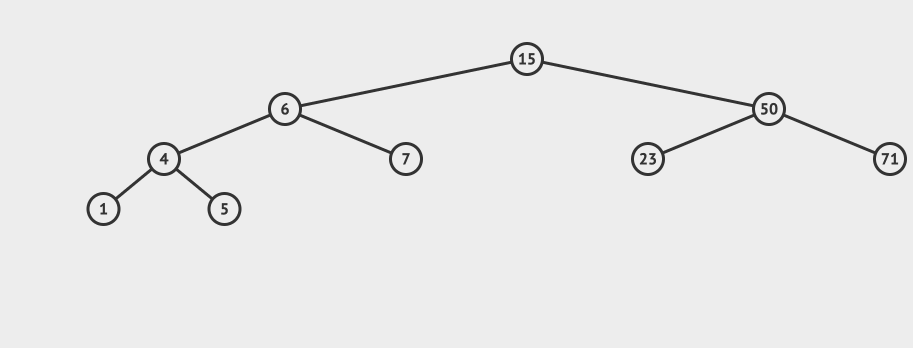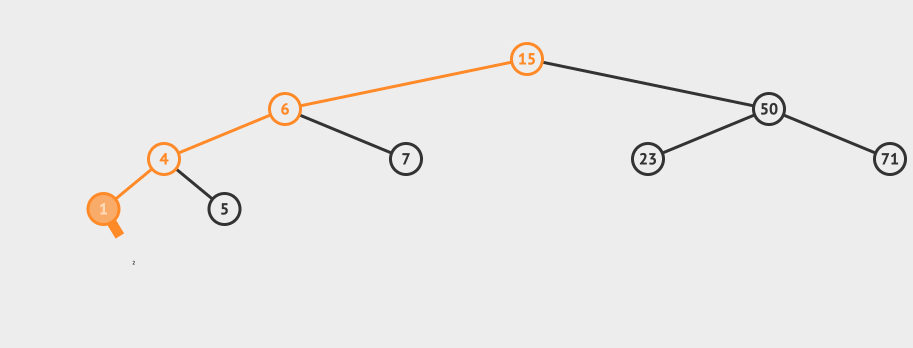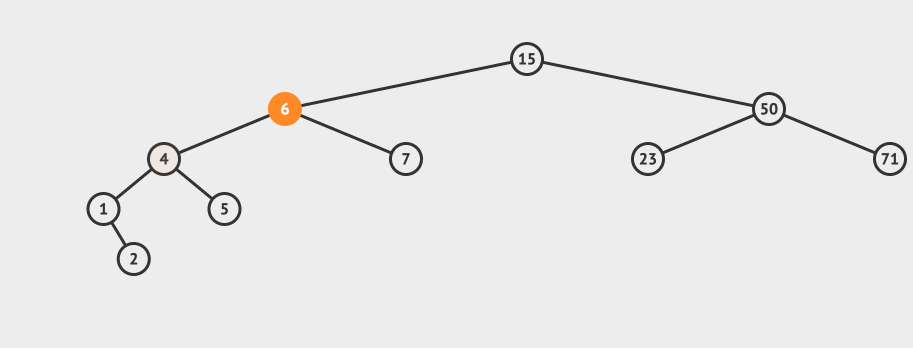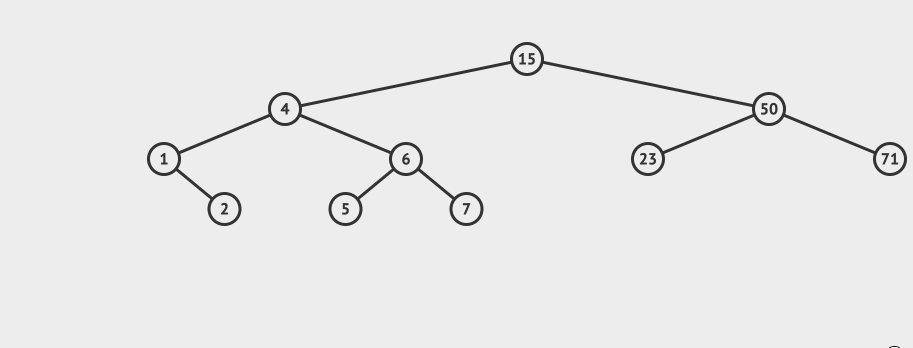
先看一个AVL的例子：

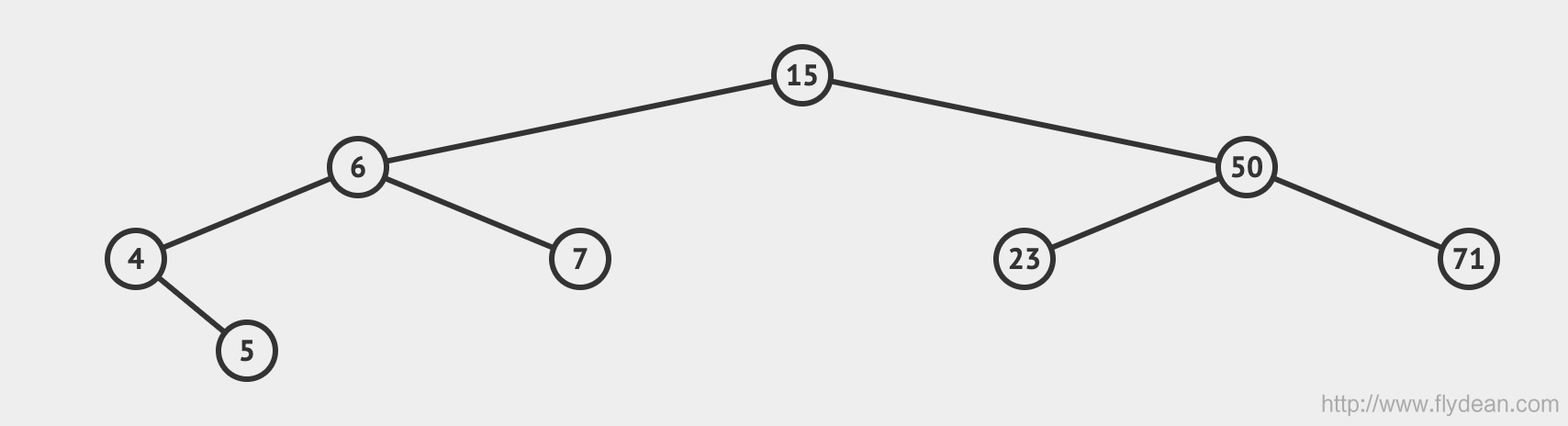
总结一下，AVL首先是一个二叉搜索树，然后又是一个二叉平衡树。

AVL的构建

有了AVL的特性之后，我们看下AVL是怎么构建的。

public class AVLTree {

    //根节点
    Node root;

    class Node {
        int data; //节点的数据
        int height; //节点的高度
        Node left;
        Node right;

        public Node(int data) {
            this.data = data;
            left = right = null;
        }
    }

同样的，AVL也是由各个节点构成的，每个节点拥有data，left和right几个属性。

因为是二叉平衡树，节点是否平衡还跟节点的高度有关，所以我们还需要定义一个height作为节点的高度。

在来两个辅助的方法，一个是获取给定的节点高度：

//获取给定节点的高度
    int height(Node node) {
        if (node == null)
            return 0;
        return node.height;
    }

和获取平衡因子：

//获取平衡因子
    int getBalance(Node node) {
        if (node == null)
            return 0;
        return height(node.left) - height(node.right);
    }

AVL的搜索

AVL的搜索和二叉搜索树的搜索方式是一致的。

先看一个直观的例子，怎么在AVL中搜索到7这个节点：

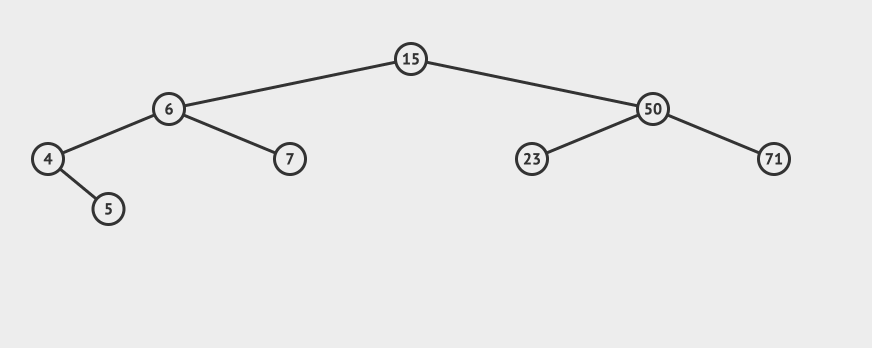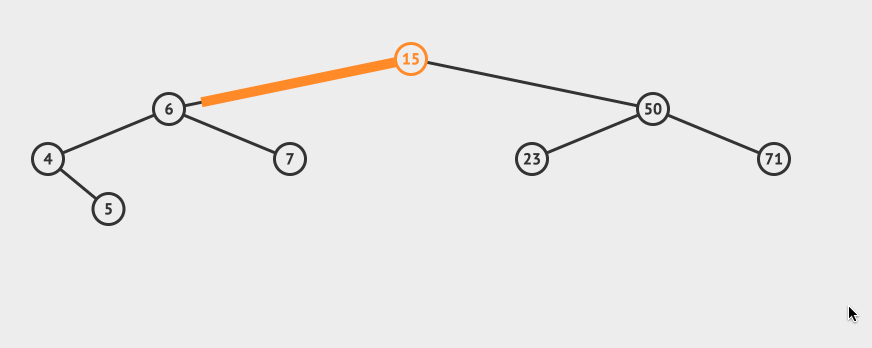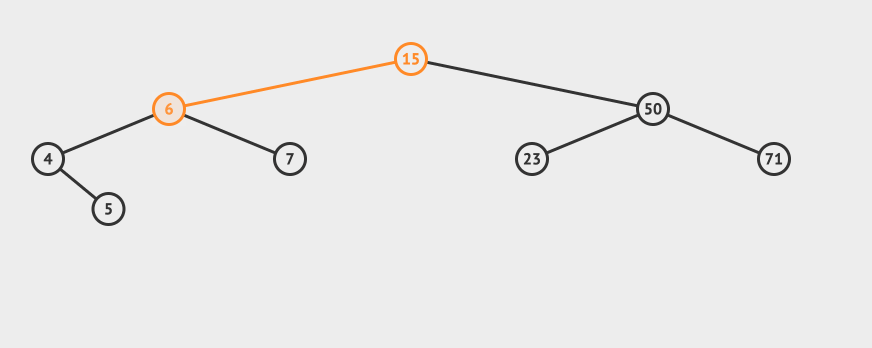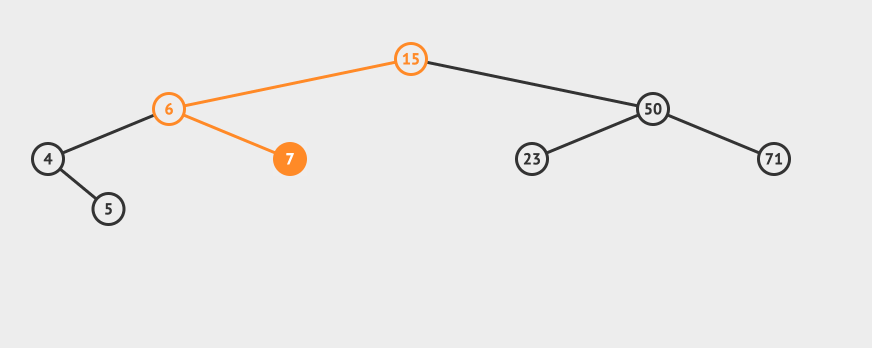
搜索的基本步骤是：

1. 从根节点15出发，比较根节点和搜索值的大小
2. 如果搜索值小于节点值，那么递归搜索左侧树
3. 如果搜索值大于节点值，那么递归搜索右侧树
4. 如果节点匹配，则直接返回即可。

相应的java代码如下：

//搜索方法，默认从根节点搜索
    public Node search(int data){
        return search(root,data);
    }

    //递归搜索节点
    private Node search(Node node, int data)
    {
        // 如果节点匹配，则返回节点
        if (node==null || node.data==data)
            return node;

        // 节点数据大于要搜索的数据，则继续搜索左边节点
        if (node.data > data)
            return search(node.left, data);

        // 如果节点数据小于要搜素的数据，则继续搜索右边节点
        return search(node.right, data);
    }

AVL的插入

AVL的插入和BST的插入是一样的，不过插入之后有可能会导致树不再平衡，所以我们需要做一个再平衡的步骤。

看一个直观的动画：

插入的逻辑是这样的：

1. 从根节点出发，比较节点数据和要插入的数据
2. 如果要插入的数据小于节点数据，则递归左子树插入
3. 如果要插入的数据大于节点数据，则递归右子树插入
4. 如果根节点为空，则插入当前数据作为根节点

插入数据之后，我们需要做再平衡。

再平衡的逻辑是这样的：

1. 从插入的节点向上找出第一个未平衡的节点，这个节点我们记为z
2. 对z为根节点的子树进行旋转，得到一个平衡树。

根据以z为根节点的树的不同，我们有四种旋转方式：

• left-left：

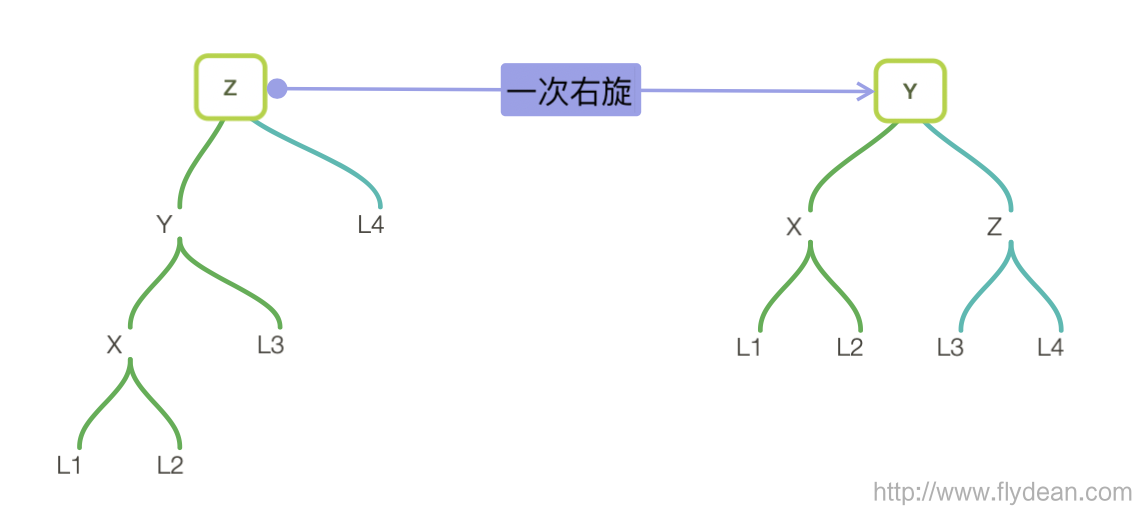
如果是left left的树，那么进行一次右旋就够了。

右旋的步骤是怎么样的呢？

1. 找到z节点的左节点y
2. 将y作为旋转后的根节点
3. z作为y的右节点
4. y的右节点作为z的左节点
5. 更新z的高度

相应的代码如下：

Node rightRotate(Node node) {
        Node x = node.left;
        Node y = x.right;

        // 右旋
        x.right = node;
        node.left = y;

        // 更新node和x的高度
        node.height = max(height(node.left), height(node.right)) + 1;
        x.height = max(height(x.left), height(x.right)) + 1;

        // 返回新的x节点
        return x;
    }

• right-right:

如果是right-right形式的树，需要经过一次左旋：

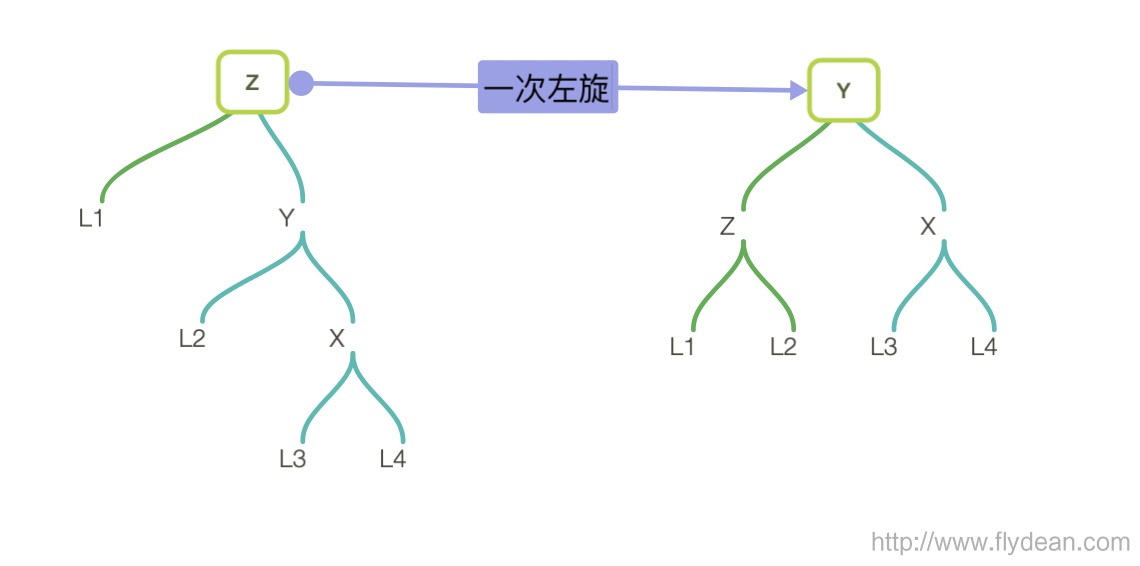
左旋的步骤正好和右旋的步骤相反：

1. 找到z节点的右节点y
2. 将y作为旋转后的根节点
3. z作为y的左节点
4. y的左节点作为z的右节点
5. 更新z的高度

相应的代码如下：

//左旋
    Node leftRotate(Node node) {
        Node x = node.right;
        Node y = x.left;

        //左旋操作
        x.left = node;
        node.right = y;

        // 更新node和x的高度
        node.height = max(height(node.left), height(node.right)) + 1;
        x.height = max(height(x.left), height(x.right)) + 1;

        // 返回新的x节点
        return x;
    }

• left-right：

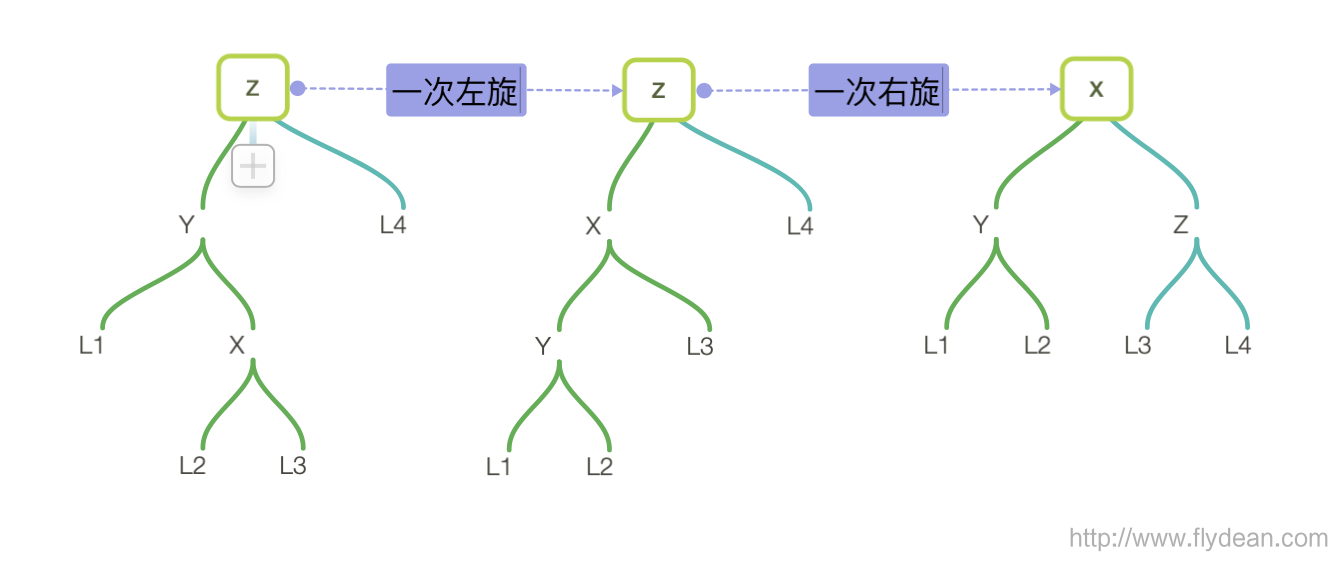
如果是left right的情况，需要先进行一次左旋将树转变成left left格式，然后再进行一次右旋，得到最终结果。

• right-left：

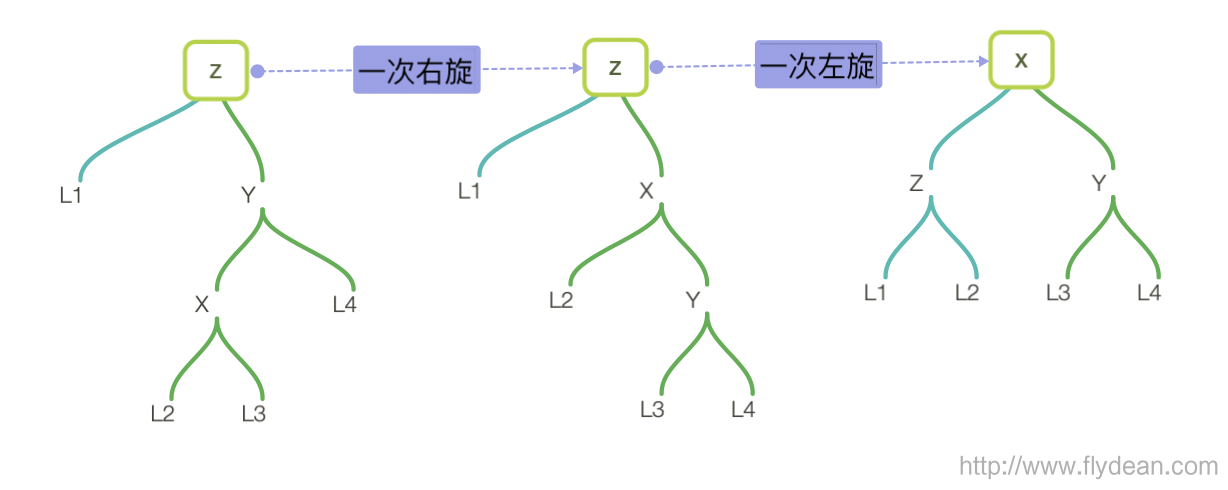
如果是right left格式，需要先进行一次右旋，转换成为right right格式，然后再进行一次左旋即可。

现在问题来了，怎么判断一个树到底是哪种格式呢？我们可以通过获取平衡因子和新插入的数据比较来判断：

1. 如果balance>1,那么我们在Left Left或者left Right的情况，这时候我们需要比较新插入的data和node.left.data的大小

   如果data < node.left.data，表示是left left的情况，只需要一次右旋即可

   如果data > node.left.data，表示是left right的情况，则需要将node.left进行一次左旋，然后将node进行一次右旋

2. 如果balance<-1,那么我们在Right Right或者Right Left的情况，这时候我们需要比较新插入的data和node.right.data的大小
   
   如果data > node.right.data，表示是Right Right的情况，只需要一次左旋即可

   如果data < node.left.data，表示是Right left的情况，则需要将node.right进行一次右旋，然后将node进行一次左旋

插入节点的最终代码如下：

//插入新节点，从root开始
    public void insert(int data){
        root=insert(root, data);
    }

    //遍历插入新节点
    Node insert(Node node, int data) {

        //先按照普通的BST方法插入节点
        if (node == null)
            return (new Node(data));

        if (data < node.data)
            node.left = insert(node.left, data);
        else if (data > node.data)
            node.right = insert(node.right, data);
        else
            return node;

        //更新节点的高度
        node.height = max(height(node.left), height(node.right)) + 1;

        //判断节点是否平衡
        int balance = getBalance(node);

        //节点不平衡有四种情况
        //1.如果balance>1,那么我们在Left Left或者left Right的情况，这时候我们需要比较新插入的data和node.left.data的大小
        //如果data < node.left.data，表示是left left的情况，只需要一次右旋即可
        //如果data > node.left.data，表示是left right的情况，则需要将node.left进行一次左旋，然后将node进行一次右旋
        //2.如果balance<-1,那么我们在Right Right或者Right Left的情况，这时候我们需要比较新插入的data和node.right.data的大小
        //如果data > node.right.data，表示是Right Right的情况，只需要一次左旋即可
        //如果data < node.left.data，表示是Right left的情况，则需要将node.right进行一次右旋，然后将node进行一次左旋

        //left left
        if (balance > 1 && data < node.left.data)
            return rightRotate(node);

        // Right Right
        if (balance < -1 && data > node.right.data)
            return leftRotate(node);

        // Left Right
        if (balance > 1 && data > node.left.data) {
            node.left = leftRotate(node.left);
            return rightRotate(node);
        }

        // Right Left
        if (balance < -1 && data < node.right.data) {
            node.right = rightRotate(node.right);
            return leftRotate(node);
        }

        //返回插入后的节点
        return node;
    }

AVL的删除

AVL的删除和插入类似。

首先按照普通的BST删除，然后也需要做再平衡。

看一个直观的动画：

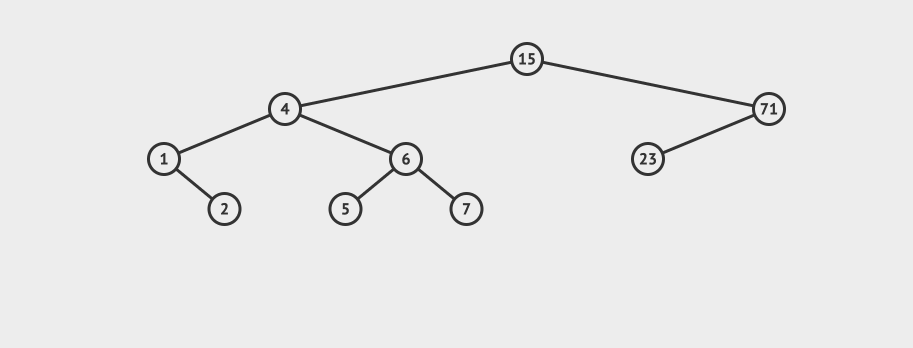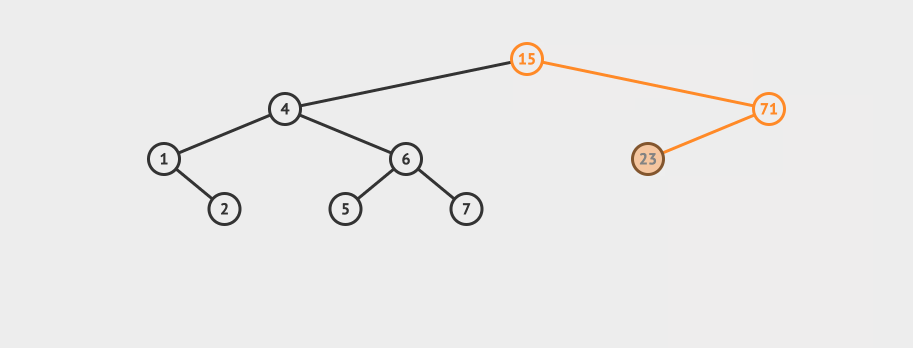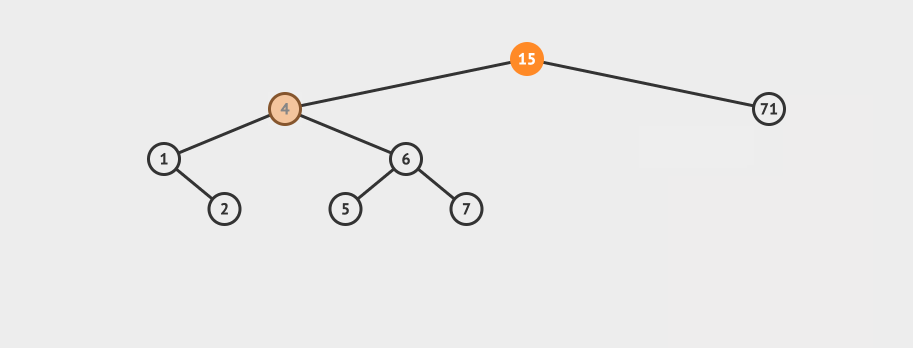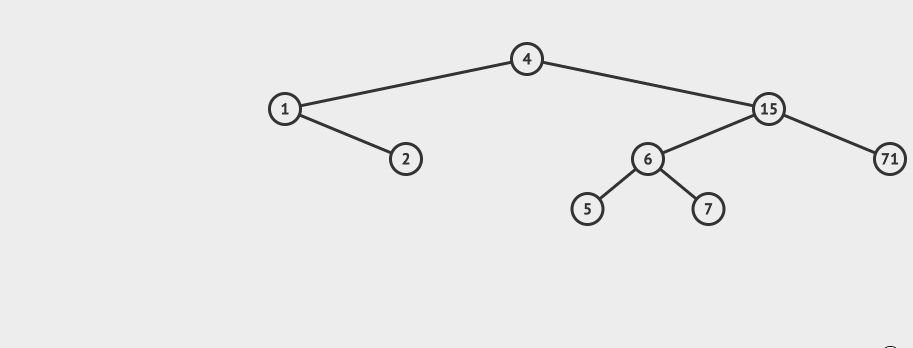
删除之后，节点再平衡也有4种情况：

1. 如果balance>1,那么我们在Left Left或者left Right的情况，这时候我们需要比较左节点的平衡因子

   如果左节点的平衡因子>=0，表示是left left的情况，只需要一次右旋即可

   如果左节点的平衡因<0，表示是left right的情况，则需要将node.left进行一次左旋，然后将node进行一次右旋

2. 如果balance<-1,那么我们在Right Right或者Right Left的情况，这时候我们需要比较右节点的平衡因子

   如果右节点的平衡因子<=0，表示是Right Right的情况，只需要一次左旋即可

   如果右节点的平衡因子>0，表示是Right left的情况，则需要将node.right进行一次右旋，然后将node进行一次左旋

相应的代码如下：

Node delete(Node node, int data)
    {
        //Step 1. 普通BST节点删除
        // 如果节点为空，直接返回
        if (node == null)
            return node;

        // 如果值小于当前节点，那么继续左节点删除
        if (data < node.data)
            node.left = delete(node.left, data);

        //如果值大于当前节点，那么继续右节点删除
        else if (data > node.data)
            node.right = delete(node.right, data);

       //如果值相同，那么就是要删除的节点
        else
        {
            // 如果是单边节点的情况
            if ((node.left == null) || (node.right == null))
            {
                Node temp = null;
                if (temp == node.left)
                    temp = node.right;
                else
                    temp = node.left;

                //没有子节点的情况
                if (temp == null)
                {
                    node = null;
                }
                else // 单边节点的情况
                    node = temp;
            }
            else
            {  //非单边节点的情况
                //拿到右侧节点的最小值
                Node temp = minValueNode(node.right);
                //将最小值作为当前的节点值
                node.data = temp.data;
                // 将该值从右侧节点删除
                node.right = delete(node.right, temp.data);
            }
        }

        // 如果节点为空，直接返回
        if (node == null)
            return node;

        // step 2: 更新当前节点的高度
        node.height = max(height(node.left), height(node.right)) + 1;

        // step 3: 获取当前节点的平衡因子
        int balance = getBalance(node);

        // 如果节点不再平衡，那么有4种情况
        //1.如果balance>1,那么我们在Left Left或者left Right的情况，这时候我们需要比较左节点的平衡因子
        //如果左节点的平衡因子>=0，表示是left left的情况，只需要一次右旋即可
        //如果左节点的平衡因<0，表示是left right的情况，则需要将node.left进行一次左旋，然后将node进行一次右旋
        //2.如果balance<-1,那么我们在Right Right或者Right Left的情况，这时候我们需要比较右节点的平衡因子
        //如果右节点的平衡因子<=0，表示是Right Right的情况，只需要一次左旋即可
        //如果右节点的平衡因子>0，表示是Right left的情况，则需要将node.right进行一次右旋，然后将node进行一次左旋
        // Left Left Case
        if (balance > 1 && getBalance(node.left) >= 0)
            return rightRotate(node);

        // Left Right Case
        if (balance > 1 && getBalance(node.left) < 0)
        {
            node.left = leftRotate(node.left);
            return rightRotate(node);
        }

        // Right Right Case
        if (balance < -1 && getBalance(node.right) <= 0)
            return leftRotate(node);

        // Right Left Case
        if (balance < -1 && getBalance(node.right) > 0)
        {
            node.right = rightRotate(node.right);
            return leftRotate(node);
        }
        return node;
    }

本文的代码地址：

learn-algorithm

本文收录于 http://www.flydean.com/11-algorithm-avl-tree/

最通俗的解读，最深刻的干货，最简洁的教程，众多你不知道的小技巧等你来发现！

欢迎关注我的公众号:「程序那些事」,懂技术，更懂你！