OO Unit1 总结

OO Unit1 总结

---

每次作业的思路和技术分析

No.1

一共写了8个类，2个接口，主要的其实只有4个类1个接口

主要接口：

• PowerFunction就是每一项去掉系数的那一部分，有求导和乘法两个方法；
  
  4个主要的：
• ItemMatcher负责将一行字符串解析；
• PolynomialInput负责从指定的InputStream一行一行读，然后利用ItemMatcher实例解析结果，创建多项式；
• SingleXPowerFunction实现了PowerFunction接口的类，表示只有一种未知数；
• Polynomial类，维护了一个map，PowerFunction为键，系数为值。

不重要的类：

• MainClass，包含main()和测试用例，单独弄出来方便测试；
• PatternMarks是enum类，方便管理正则表达式的标记；
• StringPatterns类专门用于正则表达式的生成，有一些静态的自动打包方法（添加捕获组、非捕获组、为捕获组设置标记）；
• MixUsingDifferentPowerFunctionException类是自定义的异常，是一个RuntimeException，保证多项式类只能选择一种实现了Powerfunction的类做键；
• StringProcess接口是预处理的接口，实现一个String process(String)方法，会在读入的那个类，读入一行之后先对字符串进行预处理，再进行解析。

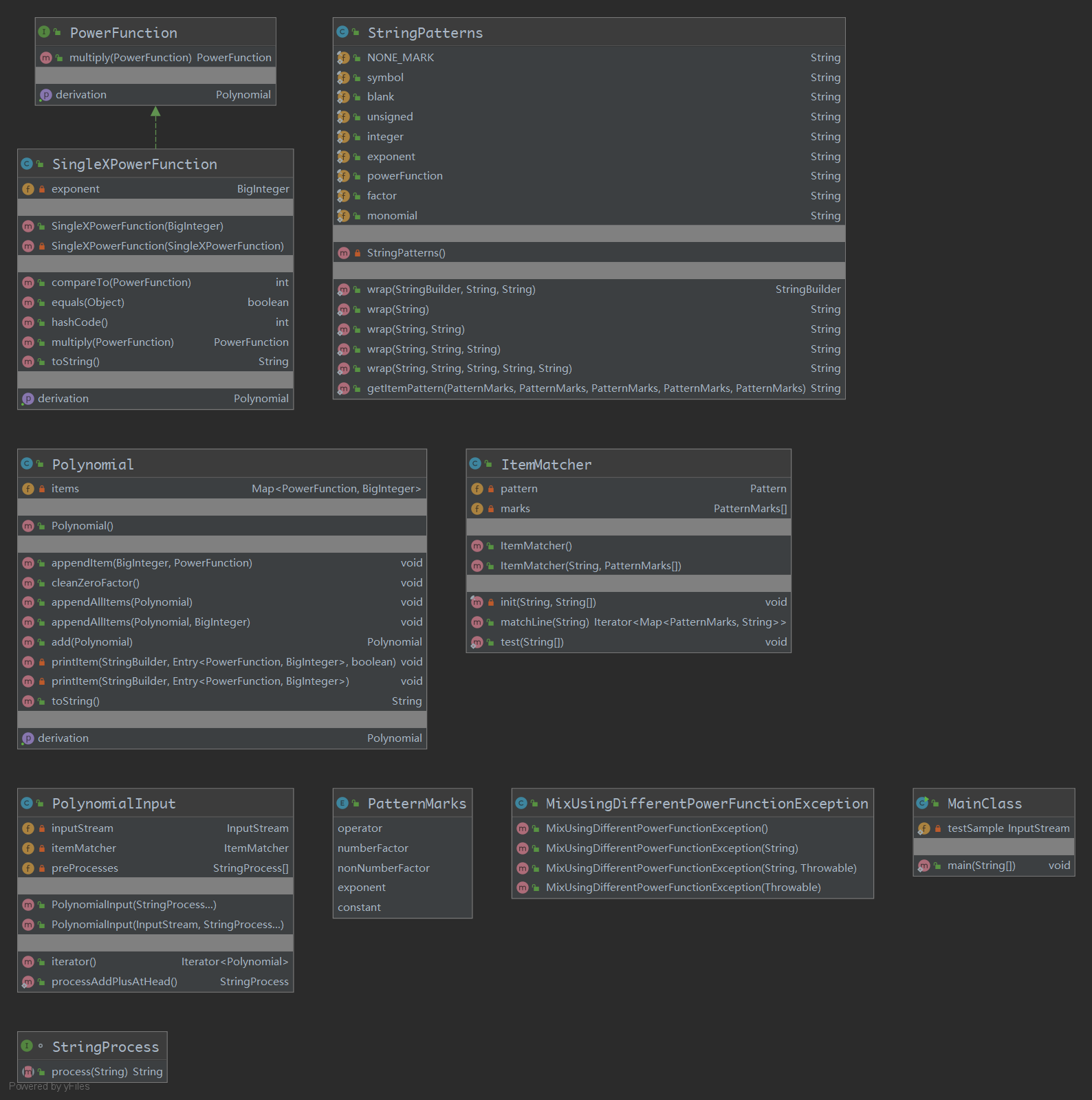
Metrics分析结果：

类名	平均圈复杂度	总圈复杂度
Polynomial	2.5	30.0
PolynomialInput	2.0	14.0
SingleXPowerFunction	1.625	13.0
ItemMatcher	1.375	11.0
StringPatterns	1.143	8.0
MixUsingDifferentPowerFunctionException	1.0	4.0
MainClass	2.0	2.0
PatternMarks		0.0
Total		82.0
Average	1.745	10.25

复杂度较高的两个类Polynomial和PolynomialInput，确实都存在很大的问题。

• 对于Polymial，问题在于输出逻辑过于复杂，不仅要判断来自内层的PowerFunction的形式，还要判断本身的正负，导致一个输出需要三个函数。（还因此导致了第一次作业互测的大量bug）
• 对于PolynomialInput，问题主要是整体的设计。这个类需要将输入的InputStream作为参数，而本身以迭代器的方式向外输出一个个多项式。它利用ItemMatcher也只是解析Matcher，还要利用ItemMatcher返回的字符串数组信息来构建多项式。将输入一行字符串、拆分字符串、构建多项式全部耦合在一起了。

No.2

这一次作业我重新分析了整个多项式的数学性质，力求构建一个比较完备的多项式体系。经过分析发现多项式的运算有如下对应关系：

项*数	项+项
项^数	项*项

每行的一组运算都满足线性空间的运算要求的8条性质（第一列对应向量数乘，第二列对应向量加法），不过要保证这两个线性空间都有零元（而且是不一样的，前者是ZERO，后者是ONE）。其实数乘可以看作若干个加法，数幂可以看作若干个乘法。

构建一个比较完备的多项式系统的关键就是项的公共基类实现加法和乘法，我采用了如下策略：

• 利用Monomial实现【乘法】维护一个Map<项,指数>
• 利用Polynomial实现【加法】维护一个Map<项,系数>

Monomial和Polynomial也都是项类的子类。

这两个类都有化简方法，把Map中同类别的项拆开，只有一个key并且value为1时会退化为key，没有key时Monomial退化为ONE，Polynomial退化为ZERO。

实现运算的方法就是new一个相应对象，然后把被运算的对象一股脑放进Map中，再化简，然后上锁（不再允许更改）。

除了M和P两个类，还需要实现一些基础的类，项类理论上都最好是不可变对象，但是M和P一般创建的时候需要比较多的操作，所以给它们留了更改的接口，然后有一个加锁的方法（无解锁方法，加锁后尝试修改会引发RuntimeException）。

基础项包括：

• 字母类：维护一个字符，有一个静态对象x
• 常项类：ZERO、ONE两个静态对象
• 三角函数类：一个sin\cos的标记，一个内部项的引用

具体实现上，有这样的细节：

• 公共基类AbstractFunction是抽象类，实现了add(BigInteger),add(AbstractFunction),multiply(BigInteger),multiply(AbstractFunction),power(BigInteger)五个方法和为了方便的重载，这些方法都是返回一个新的对象。规定了一个抽象方法getDerivation求导；
• 由于Polynomial和Monomial在行为上表现极其相似（都是用于实现某个线性空间上的运算），所以其大部分行为都可以提炼出来成为一个抽象的AbstractMutableFunction类；
• 为了提高Polynomial和Monomial的安全性，为这两个类创建了static的工厂方法valueOf，创建并将所有待加入的项加入后，化简、上锁。注意工厂方法的返回值是AbstractFunction，因为化简可能会导致类型的改变（退化）。此外，将AbstractMutableFunction类所有可以改动map内数据的方法访问性改为protected；
• 注意Polynomial参与乘法运算的时候，输出结果其实是Polymial，这要求Monomial类化简的时候，若map内有Polynomial，化简结果应该是Polynomial。

构建结果如下：

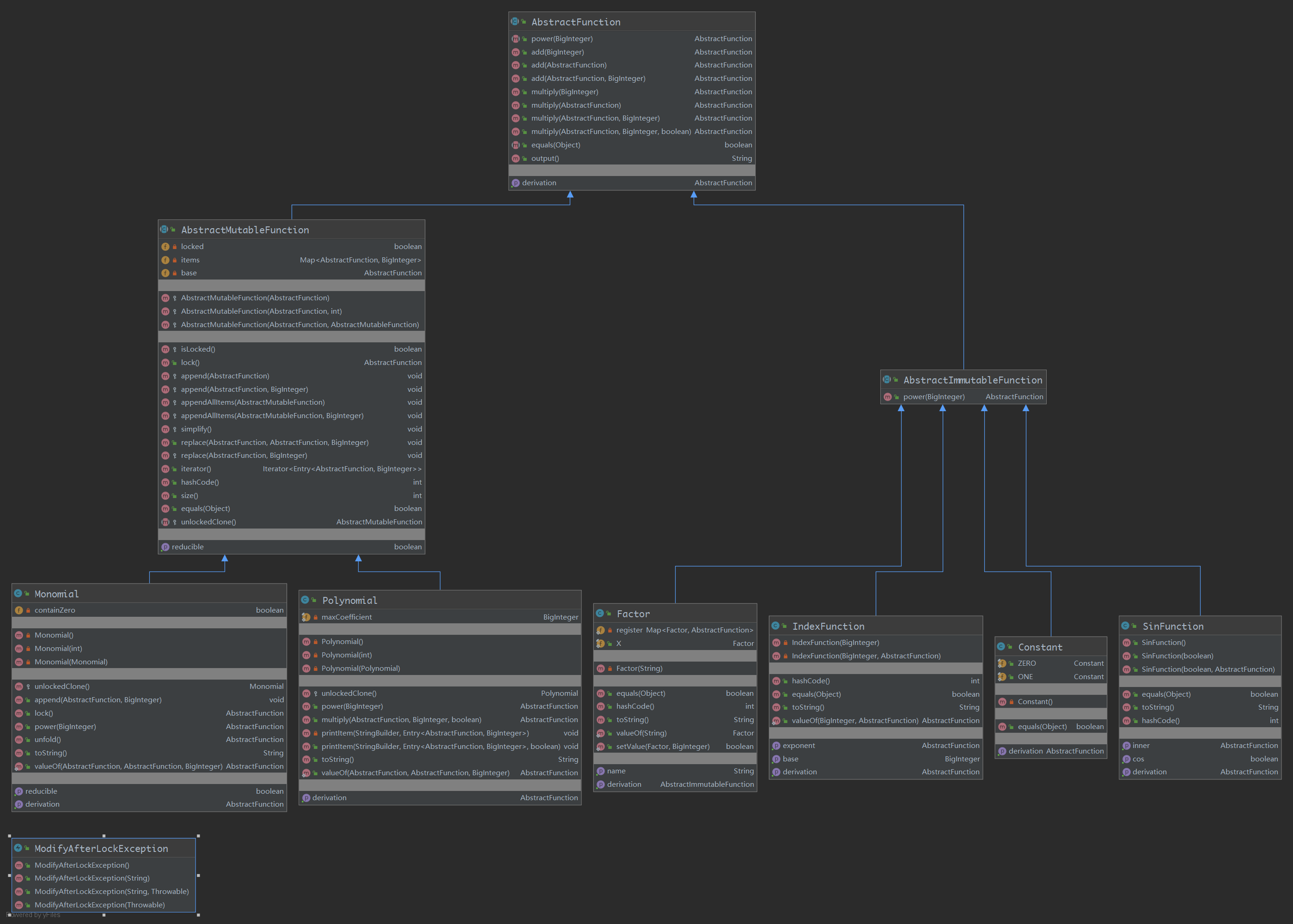
除了多项式体系之外，输入和构建部分大规模重构：

• 弃用了原来的ItemMatcher（虽然没把它删掉）；
• 把以前的PolynomialInput改为InputAnalyzer，它接收一行的String为参数，不再负责输入。它不再负责多项式的构建，将这个任务交给了FunctionFactory。它仅进行一行字符串的预处理，而这些预处理由StringProcess进行。
• 将以前的StringProcess接口更名为IStringProcess（其实是个C#命名风格），StringProcess改为一个实现了该接口的enum类，这里包括了检查格式、把原输入格式改为便于Factory处理的格式。通过InputAnalyzer+StringProcess的形式，使得预处理的执行和预处理的定义解耦，在后面要求更改后，只需在new的时候为InputAnalyzer指定其他的StringProcess组合即可，就像这样：

StringProcess[] processes = {
    StringProcess.REMOVE_SPACE,
    StringProcess.CHECK_FORMAT_TOTAL,
    StringProcess.ADD_PLUS_AT_HEAD,
    StringProcess.REPLACE_INDEX,
    StringProcess.REPLACE_SYMBOL,
    StringProcess.REPLACE_SYMBOL,
    StringProcess.CHECK_FORMAT_POWER_LIMIT
};
InputAnalyzer analyzer = new InputAnalyzer(processes);

• 更改了MainClass，它现在会先尝试寻找一个testSample.txt，若找到了，进入测试模式，从该文件读入全部测试数据，将输出结果输出，并开始记录日志；否则，从控制台进行读入，输出也只输出到控制台。

Metrics分析结果：

类名	平均圈复杂度	总圈复杂度
polynomial.FunctionFactory	3.2	16.0
polynomial.functions.Polynomial	2.455	27.0
polynomial.functions.Monomial	2.417	29.0
polynomial.functions.AbstractMutableFunction	2.167	39.0
polynomial.functions.AbstractImmutableFunction	2.0	2.0
MainClass	1.75	7.0
polynomial.functions.Factor	1.625	13.0
polynomial.functions.IndexFunction	1.556	14.0
polynomial.functions.AbstractFunction	1.5	12.0
polynomial.InputAnalyzer	1.5	3.0
polynomial.StringProcess	1.429	10.0
polynomial.ItemMatcher	1.375	11.0
polynomial.functions.SinFunction	1.333	12.0
polynomial.StringPatterns	1.1	11.0
polynomial.functions.ModifyAfterLockException	1.0	4.0
polynomial.functions.Constant	1.0	7.0
polynomial.WrongFormatException	1.0	4.0
polynomial.PatternMarks		0.0
Total		221.0

复杂度较高的几个类都是承载着核心逻辑的类。不过FunctionFactory确实过于复杂了，将各个部分拆成一步一步的函数有点随意了。

No.3

由于有了第二次作业中很完备的多项式体系，第三次作业很顺利，主要的更改来自于输入逻辑和化简逻辑。

多项式体系基本没变：

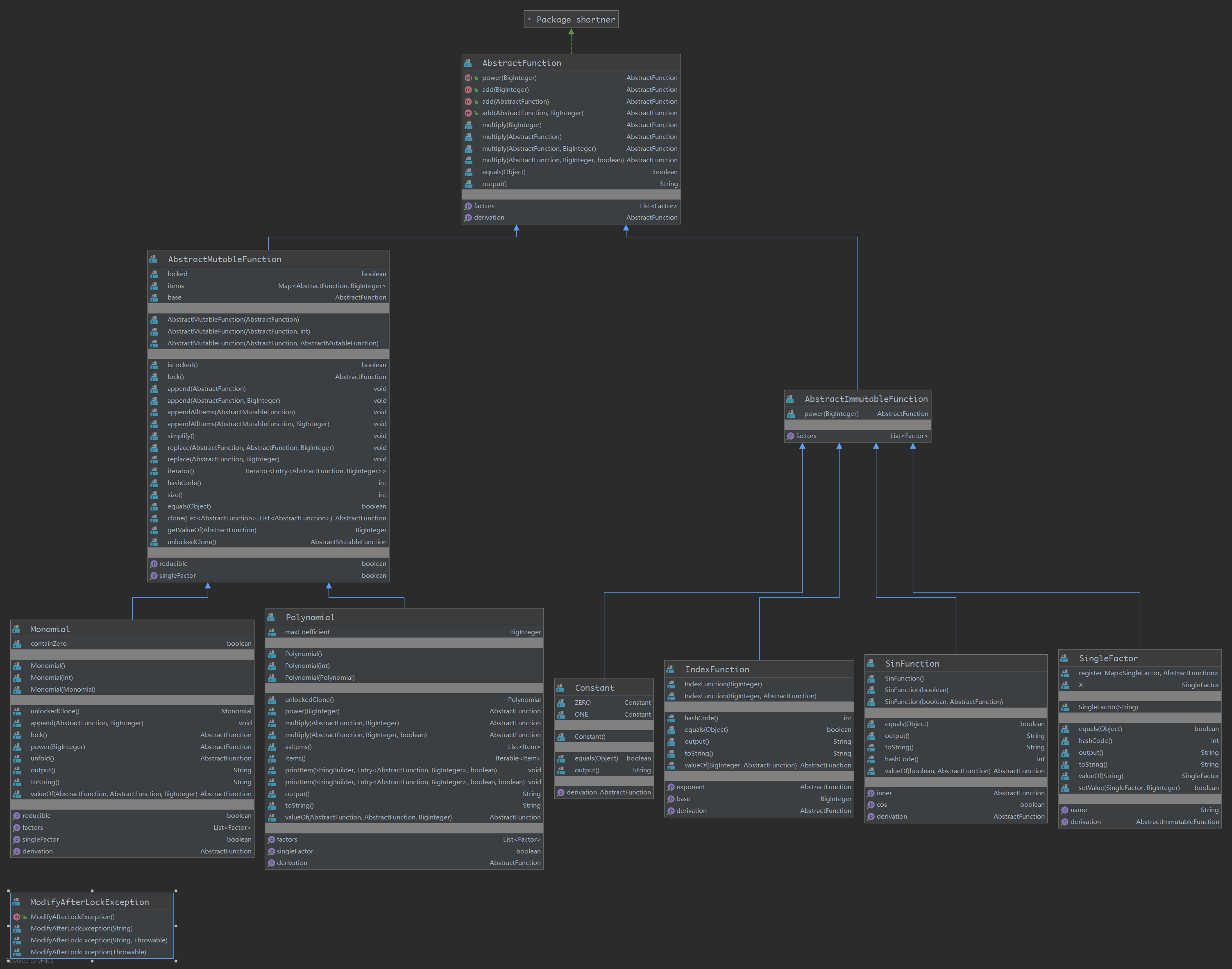
对于输入逻辑，由于有了递归的结构，所以不能一把正则进行格式检查，并且sin只能嵌套因子，不能嵌套表达式，这使得格式检查要分为表达式和因子两类。这样使得预处理和构建表达式都需要同样的嵌套顺序，所以现在将预处理和构建表达式合并在一起解决，废弃FunctionFactory，将其中的逻辑改到InputAnalyzer中。InputAnalyzer主要由四个方法：表达式的预处理、表达式解析、因子预处理、因子解析。两个解析方法都只能被预处理方法调用，预处理方法可以被随意调用，以实现嵌套的解析。

由于目前的多项式在做乘法的时候，默认是需要进行乘法分配律拆括号的，这将导致多项式长度过长，需要再进行公因式提取。现在的算法是进行穷举，穷举所有可能的公因式提取的可能，然后比较输出结果的长度，选取最短的结果进行输出。此时就发现了原有的多项式系统不利于这样的化简，因为公因式提取是以a*x**b为单位进行的，但是原来的体系把数乘和数幂分开的，所以需要引进新的体系。但是好在这个体系不需要做求导之类的事情，提取公因式的的时候也只操作最外层的Polynomial，所以很简单就能构成了。

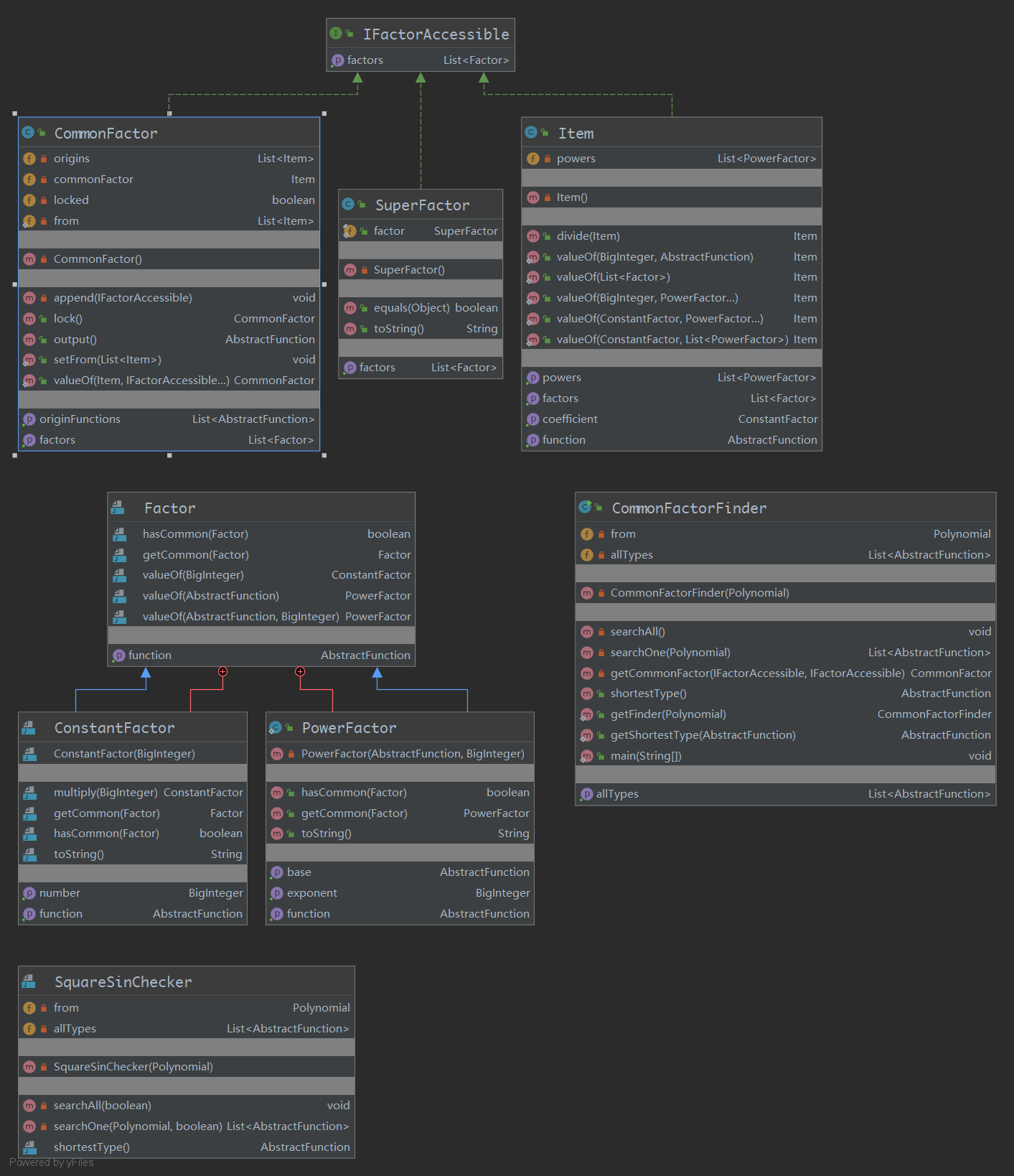
Metrics分析结果：

类名	平均圈复杂度	总圈复杂度
polynomial.functions.shortner.SquareSinChecker	3.5	14.0
polynomial.FunctionFactory	3.2	16.0
polynomial.functions.Monomial	2.867	43.0
polynomial.InputAnalyzer	2.857	20.0
polynomial.functions.shortner.CommonFactorFinder	2.554	23.0
polynomial.StringProcess	2.4	36.0
polynomial.functions.Polynomial	2.316	44.0
polynomial.functions.shortner.CommonFactor	2.25	18.0
polynomial.functions.AbstractMutableFunction	2.211	42.0
polynomial.functions.shortner.Item	1.818	20.0
polynomial.functions.IndexFunction	1.8	18.0
MainClass	1.8	9.0
polynomial.functions.SinFunction	1.727	19.0
polynomial.OutputAnalyzer	1.667	10.0
polynomial.functions.SingleFactor	1.556	14.0
polynomial.functions.AbstractImmutableFunction	1.5	3.0
polynomial.functions.shortner.Factor.ConstantFactor	1.429	10.0
polynomial.functions.shortner.Factor.PowerFactor	1.286	9.0
polynomial.functions.AbstractFunction	1.125	9.0
polynomial.StringPatterns	1.083	13.0
polynomial.functions.shortner.SuperFactor	1.0	4.0
polynomial.functions.Constant	1.0	10.0
polynomial.functions.ModifyAfterLockException	1.0	4.0
polynomial.WrongFormatException	1.0	4.0
polynomial.functions.shortner.Factor	1.0	3.0
polynomial.PatternMarks		0.0
Total		415.0

三角函数的化简因为ddl之前都没有修完bug，所以就没有使用了，从分析结果来看，其复杂度太高，也是bug没有修完的原因。因为它不仅要检查AbstractFunction的内部嵌套的类，并检查是否是sin/cos，这导致其与原来的Functions系统每个类的耦合都很高。

FunctionFactory已经被弃用了，其代替品InputAnalyzer尽管还肩负着预处理的任务，但其表现比它好得多。

CommonFactorFinder需要穷举全部公因式，所以和Polynomial、Monomial耦合都不低。

---

bug分析

这一单元我自己的bug数量控制的还可以，三次作业一共只有2个bug，一个是第一次作业没有关注输出0的情况，一个是第三次作业优化过程中陷入死循环了。这两个bug都是边界条件所致。

这一单元我主动hack别人的表现确实不佳，我觉得很大的原因是因为我没有构建自动测试系统，全靠人力测试，是在太慢了。但是我人肉发现的bug，很多都是边界条件，比如指数的边界、化简为0的情况等。第一次作业就是没有考虑化简结果为0的情况，导致被hack10多次（但全是这一个问题，所以一次就修复了）。以后可能需要构建测试机了。

---

面向过程→面向对象

第一次作业虽然有点面向对象的想法，但是实际上还是面向过程的偏多一些。第二次作业从线性代数的这是种寻找对象的行为和交互方式，先不管本次作业的主要逻辑（求导），先构造好类的体系，设计好它们的加减运算。最后再根据业务逻辑，利用这些构造好的体系完成业务（具体分析过程写在No.2中了，就不复制了）。

---

收获

• 总体结构要想明白了再敲键盘。由于第二次想明白了多项式的系统应该怎么构建，并且构造了一个足够完美的系统，使得，第三次在这一方面花费的精力大大减少（据我所知很多同学第三次作业都在重新构建这个系统花费了大量时间）。
• 算法也要想明白了再敲键盘。提取公因式的算法就是因为最开始没有想好，导致频繁陷入死循环（无法停止穷举）。后来仔细思考了穷举的算法，利用队列一个一个检查，分析了新的算法不会出现重复的情况。
• 从现实中的只是体系寻找类的行为方式、交互方式。这次作业我利用了线性代数的知识帮我构建了一个运算封闭的多项式系统，复杂、功能多，同时bug又少。
• 这辈子都没有过在这么短的时间内写这么多代码的经历。（上次这么多还是基物实验课的虚拟仿真实验的设计，但是这个写了好久呢）