DH算法图解+数学证明

前几天和同事讨论IKE密钥交换流程时，提到了Diffie-Hellman交换。DH算法最主要的作用便是在不安全的网络上成功公共密钥(并未传输真实密钥)。但由于对于DH算法的数学原理则不清楚，因此私下对DH算法进行一个简单学习。

1. DH算法的交互流程：

• Alice和Bob都有一个只有自己知道的私钥，在特定规则(g, a, p)下生成自己的公钥A;
• Alice将自己的公钥A，连同g, p共同发给Bob
• Bob在收到Alice发送来的公钥A, g, p后，先使用相同的规则((g, a, p))生成自己的公钥B;在使用Alice的公钥A计算生成共享密钥K
• Bob将自己的公钥B发送给Alice即可。(Alice已经有g, p, 因此无需在发送)
• Alice在接收到Bob的公钥B后,使用相同的规则计算成功共享密钥K

至此，Alice 和 Bob便同时拥有了共享密钥K。此时由于各自的私钥a,b未在互联网上传播，因此即使存在窥探者Eve，他仅通过公开的A\B\g\p在短时间内无法破解出a,b,K。因此DH算法便可以在不安全的网络上协商出密钥，基于此构建安全的加密通道。

2. 疑问：Alice和Bob最后计算的K值一样吗？

对于DH整个交互流程来说，比较简单，基本都可以理解。但是忽然说最后的K值相等，这多少有点突然和难以置信，让人有点猝不及防。

书本上都是这样解释的：

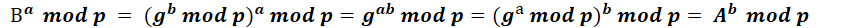
所以Alice和Bob的共享密钥K是相同的。但是，总感觉没有get到要领和精髓。因为我不知道mod（求余）的运算规则，不知道如下等式是否成立？？？

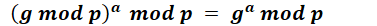
因此半夜凌晨1点从刚暖热乎的被窝又爬了出来，想要证明下他们给的公式是否正确( 其实当成定理记住也就OK了，不过我嘛，还是爬起来了)。证明这个公式也很简单：将求余运算转换为加减乘除运算，然后利用二项式展开公式便可以得到答案。

至于为什么要将求余运算转换为加减乘除四则运算，原因是我不知道求余算法的规则，不然我也不需要多此一举了。

证明开始：

令:

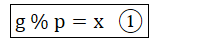
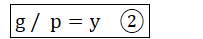
则：

根据①②式可得：

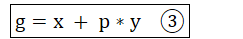
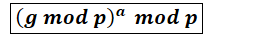
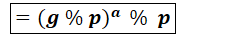
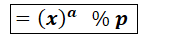
将③带入上式可得：

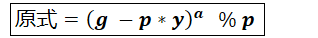
使用二项式展开公式将 −∗ 展开,则有

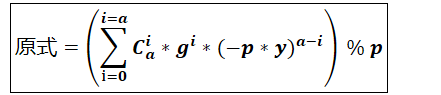
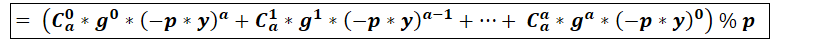
从这个表达式可以看出，前a项(i∈[0,−1])每一项都是p的整数倍，因此求余运算时必定为0，因此：

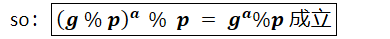
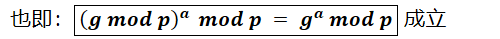
这下好了，高兴的睡不着觉了。