洛谷P1003 铺地毯 模拟

这一题就是一个很普通的模拟，每次输入的时候存储四个角的值

把四个角的横纵坐标存储在一排。然后在倒序遍历一遍，查找的时候就看所要查找的坐标在不在这个范围内，如果找到了就标记一下再输出，如果没有找到就输出-1；时间复杂度只有O(n);

题目描述

为了准备一个独特的颁奖典礼，组织者在会场的一片矩形区域（可看做是平面直角坐标系的第一象限）铺上一些矩形地毯。一共有 n张地毯，编号从 1 到n。现在将这些地毯按照编号从小到大的顺序平行于坐标轴先后铺设，后铺的地毯覆盖在前面已经铺好的地毯之上。

地毯铺设完成后，组织者想知道覆盖地面某个点的最上面的那张地毯的编号。注意：在矩形地毯边界和四个顶点上的点也算被地毯覆盖。

输入格式

输入共 n+2n + 2n+2 行。

第一行，一个整数 nnn，表示总共有 nnn 张地毯。

接下来的 n 行中，第 i+1行表示编号 iii 的地毯的信息，包含四个正整数 a,b,g,k每两个整数之间用一个空格隔开，分别表示铺设地毯的左下角的坐标 (a,b) 以及地毯在 x 轴和y 轴方向的长度。

第 n+2行包含两个正整数 x和 y，表示所求的地面的点的坐标 (x,y)。

输出格式

输出共 1行，一个整数，表示所求的地毯的编号；若此处没有被地毯覆盖则输出 -1。

输入输出样例

输入 #1 复制

3
1 0 2 3
0 2 3 3
2 1 3 3
2 2

输出 #1 复制

3

输入 #2 复制

3
1 0 2 3
0 2 3 3
2 1 3 3
4 5

输出 #2 复制

-1

说明/提示

【样例解释 1】

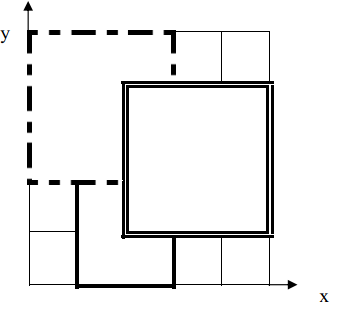
如下图，111 号地毯用实线表示，222 号地毯用虚线表示，333 号用双实线表示，覆盖点 (2,2)(2,2)(2,2) 的最上面一张地毯是 333 号地毯。

【数据范围】

对于 30% 的数据，有 n≤2n \le 2n≤2。
对于 50% 的数据，0≤a,b,g,k≤1000 \le a, b, g, k \le 1000≤a,b,g,k≤100。
对于 100%的数据，有 0≤n≤1040 \le n \le 10^40≤n≤104, 0≤a,b,g,k≤1050 \le a, b, g, k \le {10}^50≤a,b,g,k≤105。

noip2011 提高组 day1 第 111 题

这一题就是一个很普通的模拟，每次输入的时候存储四个角的值

把四个角的横纵坐标存储在一排。然后在倒序遍历一遍，查找的时候就看所要查找的坐标在不在这个范围内，如果找到了就标记一下再输出，如果没有找到就输出-1；时间复杂度只有O(n);

比如样例1

　　　　　　　　3
　　　　　　　　1 0 2 3
　　　　　　　　0 2 3 3
　　　　　　　　2 1 3 3
　　　　　　　　2 2　　　　查找的是（2，2）我们在输入的时候存储的方式是这样的↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓　

　　　　　　　　　　我们把每次的输入存储在一个二维数组里，就