P2341 [USACO03FALL][HAOI2006]受欢迎的牛 G 题解

CSDN同步

原题链接

POJ的链接

简要题意：

给定一张图，求多少个点，每个点都能到达它。

本题作为强连通分量的入门题。

何为强连通分量？有什么用？

下面一一解释。

首先，我们要确认，这道题目如果不用强连通分量而用其它方法（比如说暴力）的话：

时间复杂度将达到 \(O(n^2)\)，此时不易通过，也非正解。

强连通分量是什么？我们来看一张图吧。

我们希望，如果能把环通过某种方式去掉，然后变成有向无环图，就很容易了。

一个强连通分量中的点两两可达。（有向图中）一个点也可以被认为是一个强连通分量。

也就是说，你会发现，一个环 或者 若干个相交的环 都会变成一个强连通分量。

显然它们两两可达，最后图会变成若干个强连通分量。

你会发现，\(1\) 是一个强连通分量，\(2,3,4,5\) 是一个强连通分量，\(6\),\(7\),\(8\) 均为一个单独的强连通分量。

此时我们可以简化这个图变成：

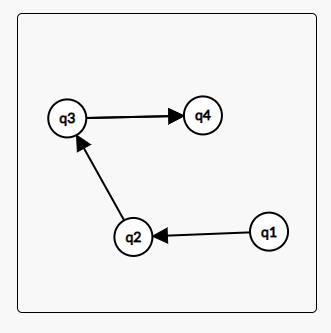
\(qx\) 表示 \(x\) 号强连通分量。

此时你发现 \(q4\) 就是答案，里面装的是 \(7\)，所以答案为 \(1\).

那么问题在于，如何求强连通分量？

回到这个图。

用 \(dfn_i\) 表示 \(i\) 的遍历编号（就是我们常说的 “时间戳”），\(f_i\) 为 \(i\) 号节点属于的强连通分量编号，\(low_i\) 为 \(i\) 号节点能走到的 \(dfn\) 值最小的节点。

一开始 \(low_i = i (1 \leq i \leq n)\).

首先，我们从 \(1\) 节点开始遍历，走到 \(2\).

然后走到了 \(3,4,5\) ，没有问题。此时 \(dfn_i = i (1 \leq i \leq 5)\)

然后，\(5\) 走到 \(2\) ，说明什么？

说明出现了环，说明出现了一个强连通分量（不一定完整，也就是不一定是一个完整的强连通分量）！

此时，\(dfn_i = 2 (3 \leq i \leq 5)\)，这是需要更新的。那么此时第一个强连通分量产生了：

\(low_i = 1 (2 \leq i \leq 5)\).

然后你回溯，发现 \(5\) 没有其它节点可走。因为它属于一个未确定的强连通分量，因此保留。

同样，回溯到 \(4\)，继续到 \(3\)，走到了 \(6\).

继续走到 \(7\). 此时 \(7\) 没有其它节点可走，并且 \(low_7 = 7\)，说明 它只能走到自己，也不存在别人能走到它——因为它没有节点可走。所以它是一个单独的强连通分量，我们把它标记，即丢弃。

然后，回溯到 \(6\).发现 \(6\) 也没有其它节点可走（\(7\) 已经被标记丢弃了），所以同理，\(6\) 也是一个强连通分量，标记丢弃掉。

接着回溯到 \(3\)，回溯到 \(2\).

然后 \(2\) 走到了 \(8\)，发现 \(8\) 也没有其它节点可走（\(7\) 已经被标记丢弃了），所以同理，\(8\) 也是一个强连通分量，标记丢弃掉。

然后回溯到 \(2\)，发现 \(2\) 没有可以走的节点了。所以，和 \(2\) 出于同一个强连通分量的节点全部被标记丢弃掉。

此时回溯到 \(1\)，\(1\) 也作为了一个单独的强连通分量。

此时强连通分量就求出来了。

那么你会说，这些过程有一个难维护的细节：就是 “同一个强连通分量的节点全部被标记丢弃掉”，难道还要扫一遍吗？

不用。我们可以用栈维护。每走过一个节点进栈，标记丢弃则出栈。

inline void dfs(int u) {
	dfn[u]=low[u]=++times;
	s.push(u); h[u]=1;
	for(int i=0,t;i<G[u].size();i++) {
		t=G[u][i];
		if(!dfn[t]) {
			dfs(t); low[u]=min(low[u],low[t]); // 如果 t 能往上，那么 u 也能
		} else if(h[t]) low[u]=min(low[u],dfn[t]); // 否则直接统计
	}
	if(low[u]==dfn[u]) { //表示当前节点无法向上，则统计答案
		cnt++; int k;
		do {
//			a[cnt].push_back(s.top());
			k=s.top();
			h[k]=0; f[k]=cnt;
			gs[cnt]++; s.pop();
		} while(k!=u) ;
	}
}

此时，重构的图（代码中未重构）

那么，如何维护最终的答案？

你会发现，如果按照强连通分量重新构图，则一定是 有向无环图 。（不一定是树，因为有可能是菱形状）

下面证明两个结论：

• 如果有 \(\geq 2\) 个点出度为 \(0\)，则整张图不存在答案。

证明：

如果有 \(\geq 2\) 个点出度为 \(0\)，则首先除了这 \(2\) 个点外的其它所有点都不会是答案。因为这 \(2\) 个点就无法到达它们。

然后，这两个点也不是答案。因为，它们互相无法到达，也就促使了互相都不是答案。得证。

• 如果只有 \(1\) 个点出度为 \(0\)，则这个答案就是它。

证明：

首先 \(y\) 不连向其它任何点，所以，整张图的答案要么是它，要么不是它。

如果这个结论不成立的话，结合上面的结论，你会发现答案始终为 \(0\).

但是样例告诉我们，不是这样的。所以得证。

这个证明可能有点不太严谨，但是考场上这样证就足够了

但是我们不需要重构这个图。

因为，我们这需要在原图上查边 \(u \rightarrow v\)，如果 \(f_u \not = f_v\)，说明不属于同一个强连通分量，就 \(du_{f_u} \gets du_{f_u} + 1\)，\(du_i\) 表示第 \(i\) 个强连通分量 缩点后 的出度。

另：把每个强连通分量看做一个点，这样的方法叫做缩点。

最后统计出度即可。

时间复杂度：\(O(n + m)\).

实际得分：\(100pts\).

#pragma GCC optimize(2)
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<vector>
#include<stack> //由于 POJ 不支持万能头，因此要手写
using namespace std;

const int N=1e5+1;

inline int read(){char ch=getchar();int f=1;while(ch<'0' || ch>'9') {if(ch=='-') f=-f; ch=getchar();}
	int x=0;while(ch>='0' && ch<='9') x=(x<<3)+(x<<1)+ch-'0',ch=getchar();return x*f;}

bool h[N]; int cnt=0;
int times,dfn[N],du[N];
int low[N],n,m,f[N],gs[N];
vector<int>G[N];
stack<int>s;

inline void dfs(int u) {
	dfn[u]=low[u]=++times;
	s.push(u); h[u]=1;
	for(int i=0,t;i<G[u].size();i++) {
		t=G[u][i];
		if(!dfn[t]) {
			dfs(t); low[u]=min(low[u],low[t]);
		} else if(h[t]) low[u]=min(low[u],dfn[t]);
	}
	if(low[u]==dfn[u]) {
		cnt++; int k;
		do {
//			a[cnt].push_back(s.top());
			k=s.top();
			h[k]=0; f[k]=cnt;
			gs[cnt]++; s.pop();
		} while(k!=u) ;
	}
} //Tarjan 模板

int main(){
	n=read(),m=read();
	while(m--) {
		int x=read(),y=read();
		G[x].push_back(y);
	} for(int i=1;i<=n;i++)
		if(!dfn[i]) dfs(i);
	for(int u=1;u<=n;u++)
	for(int i=0;i<G[u].size();i++) {
		int x=G[u][i];
		if(f[u]-f[x]) du[f[u]]++;
	}
//	for(int i=1;i<=n;i++) printf("%d ",f[i]); putchar('\n');
//	for(int i=1;i<=cnt;i++) printf("%d ",gs[i]); putchar('\n');
//	for(int i=1;i<=n;i++) printf("%d ",du[i]); putchar('\n');
	int ans=0;
	for(int i=1;i<=cnt;i++)
		if(!du[i]) {
			if(ans) {puts("0");return 0;} //已经有入度为 0 的，再来一个，答案为 0，结束
			ans=i; //记录入度为 0 强连通分量的编号
		}  printf("%d\n",gs[ans]); //强连通分量的大小即为答案
	return 0;
}