DQN（Deep Q-learning）入门教程（五）之DQN介绍

简介

DQN——Deep Q-learning。在上一篇博客DQN（Deep Q-learning）入门教程（四）之Q-learning Play Flappy Bird 中，我们使用Q-Table来储存state与action之间的q值，那么这样有什么不足呢？我们可以将问题的稍微复杂化一点了，如果在环境中，State很多，然后Agent的动作也很多，那么毋庸置疑Q-table将会变得很大很大（比如说下围棋），又或者说如果环境的状态是连续值而不是离散值，尽管我们可以将连续值进行离散化，但是又可能会导致q-table变得庞大，并且可能还有一个问题，如果某一个场景没有训练过，也就是说q-table中没有储存这个值，那么当agent遇到这种情况时就会一脸懵逼。

这个时候我们联想我们在神经网络中学到的知识，我们可以将Q-table变成一个网络模型，如下所示：（图来自莫烦）

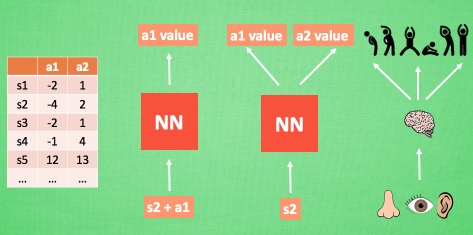
以前我们想获得Q值，需要去q-table中进行查询，但是现在我们只需要将状态和动作（或者仅输入状态）即可获得相对应的Q值，这样，我们在内存中仅仅只需要保存神经网络模型即可，简单又省内存儿。

如果不了解神经网络的话，可以先去看一看相关的知识，或者看一看我之前的博客，里面包含了相关的介绍以及具体的实例使用：

神经网络中有两个很重要的概念：训练，预测。预测我们很好理解，就是输入一个状态$s_1$，它会返回对应的$q(s_1,a_1),q(s_1,a_2) \cdots q(s_1,a_n)$，然后我们选择最大值对应的Action就行了。那么我们怎么进行训练呢？

神经网络的训练

在传统的DNN or CNN网络中，我们是已知训练集，然后进多次训练的。但是在强化学习中，训练集是未知的，因为我们的要求是机器进行自我学习。换句话来说，就是神经网络的更新是实时的，一边进行游戏得到数据集一边使用数据进行训练。

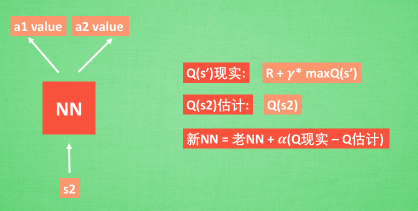
首先我们假设模型是下图这样的：输入一个 $s$ 返回不同动作对应的 $q$ 值。

那么我们进行训练的时候，$x\_train$ 即为状态 $s_1$ ，$y\_train$ 则为 $q(s_1,a_1),q(s_1,a_2) \cdots q(s_1,a_n)$。，现在的问题就回到了我们如何得到“真实”的 $y\_train$ 。在DQN（Deep Q-learning）入门教程（三）之蒙特卡罗法算法与Q-learning算法中我们提到使用如下的公式来更新q-table：

\[{\displaystyle Q^{new}(s_{t},a_{t})\leftarrow \underbrace {Q(s_{t},a_{t})} _{\text{旧的值}}+\underbrace {\alpha } _{\text{学习率}}\cdot \overbrace {{\bigg (}\underbrace {\underbrace {r_{t}} _{\text{奖励}}+\underbrace {\gamma } _{\text{奖励衰减因子}}\cdot \underbrace {\max _{a}Q(s_{t+1},a)} _{\text{estimate of optimal future value}}} _{\text{new value (temporal difference target)}}-\underbrace {Q(s_{t},a_{t})} _{\text{旧的值}}{\bigg )}} ^{\text{temporal difference}}}
\]

对应的图如下所示：

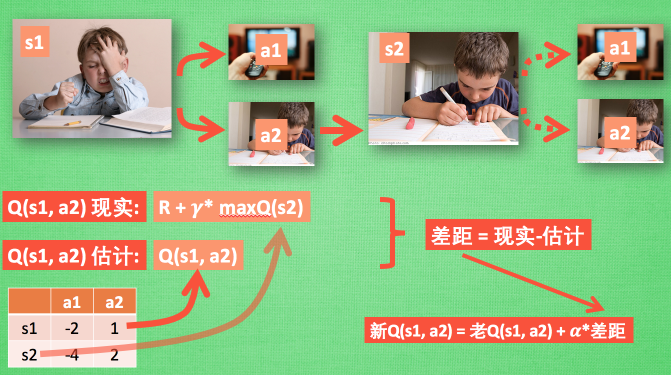
其中我们将$Q(s_1,a_1) = R+\gamma^{*} \max Q(s_2)$称之为Q现实，q-table中的$Q(s_1,a_1)$称之为Q估计。然后计算两者差值，乘以学习率，然后进行更新Q-table。

我们可以想一想神经网络中的反向传播算法，在更新网络权值的时候，我们是得到训练集中的真实值和预测值之间的损失函数，然后再乘以一个学习率，再向前逐渐地更新网络权值。这样想一想，似乎两者之间很相似。

在DQN中我们可以这样做：

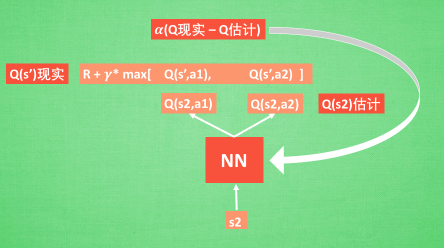
具体的使用，可以看一看下一篇博客的具体使用，用代码来表达更加的丝滑。

经验回放（Experience Replay）

经验回放是一个很妙的方法。实际上，我们训练神经网络模型需要训练很多次才可以得到一个比较好的模型，也就是说，数据会被重复的填入到神经网络中训练很多次。而经验回放就是将数据进行保存，比如说agent再$S_1$状执行动作$a_1$得到了$r_1$的奖励，然后状态转移到了$S_2$，则经验池就会将$(S_1,a_1,r_1,S_2)$进行保存，然后我们在训练的时候，随机从经验池中抽取一定数量的数据来进行训练。这样就可以不停的优化网络模型。

如果没有经验回放，我们则需要每次得到一个数据，则就进行训练，我们每次训练的内容都是目前的数据。但是，有了经验回放，我们就可以从历史数据中选择数据进行训练。

算法流程

下面介绍一下算法流程：

下面是来自Playing Atari with Deep Reinforcement Learning论文中算法流程：

下面是来自强化学习（八）价值函数的近似表示与Deep Q-Learning对算法的中文翻译：

总结

以上便是DQN的介绍，实际上DQN还有很多优化算法，比如说 Nature DQN使用两个Q网络来减少相关性，Double DQN（DDQN，Nature DQN的优化）……

下一篇博客将具体的使用DQN进行训练，同时DQN入门博客也就快结束了。

参考