I、恋爱之子

链接：https://ac.nowcoder.com/acm/contest/3570/I

来源：牛客网

题目描述

最近ZSC和他的女朋友NULL吵架了。因为ZSC是一个直男，他不知道该怎么办，于是他寻求恋爱之子磊子哥的帮助。“比起磊子，我更需要女朋友”/doge。

矛盾就如一条条线，纠在一起，越来越乱，ZSC和NULL的矛盾可以看作二维直角坐标系，在平面中有N条线段,线段的两个端点的坐标分别是 pi_x,pi_y和qi_x,qi_y。当两个线段有至少一个公共点时，就认为它们是相连的。事情往往都有关联，所以通过相连的线段连在一起的两条线段也是相连的。

恋爱之子磊子哥每次祈祷都可以消除一条线段以及所有与它相连的线段，自从磊子哥成为恋爱之子后特别忙，现在他向你求助“那你能帮帮我吗，我想知道我最少要祈祷几次才能消除所有线段”。学过算法的你，能帮助磊子哥求出最少的次数吗？

输入描述:

输入第一行是一个整数N(1≤N≤4∗103)，表示线段的个数，接下来N行，每行四个整数pi_x,pi_y和qi_x,qi_y表示该线段的两个端点坐标。

输出描述: 输出最少需要的祈祷数。

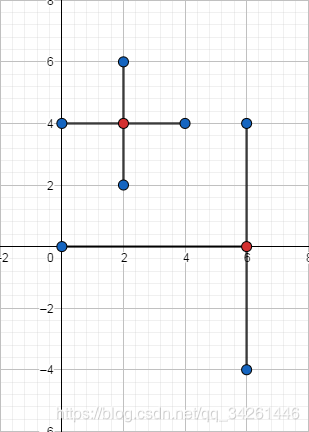
示例1
输入
复制
4
0 0 6 0
6 -4 6 4
0 4 4 4
2 2 2 6
输出
2

说明

示例2
输入
复制
3
0 1 1 0
0 2 2 0
0 3 3 0
输出
复制
3
说明

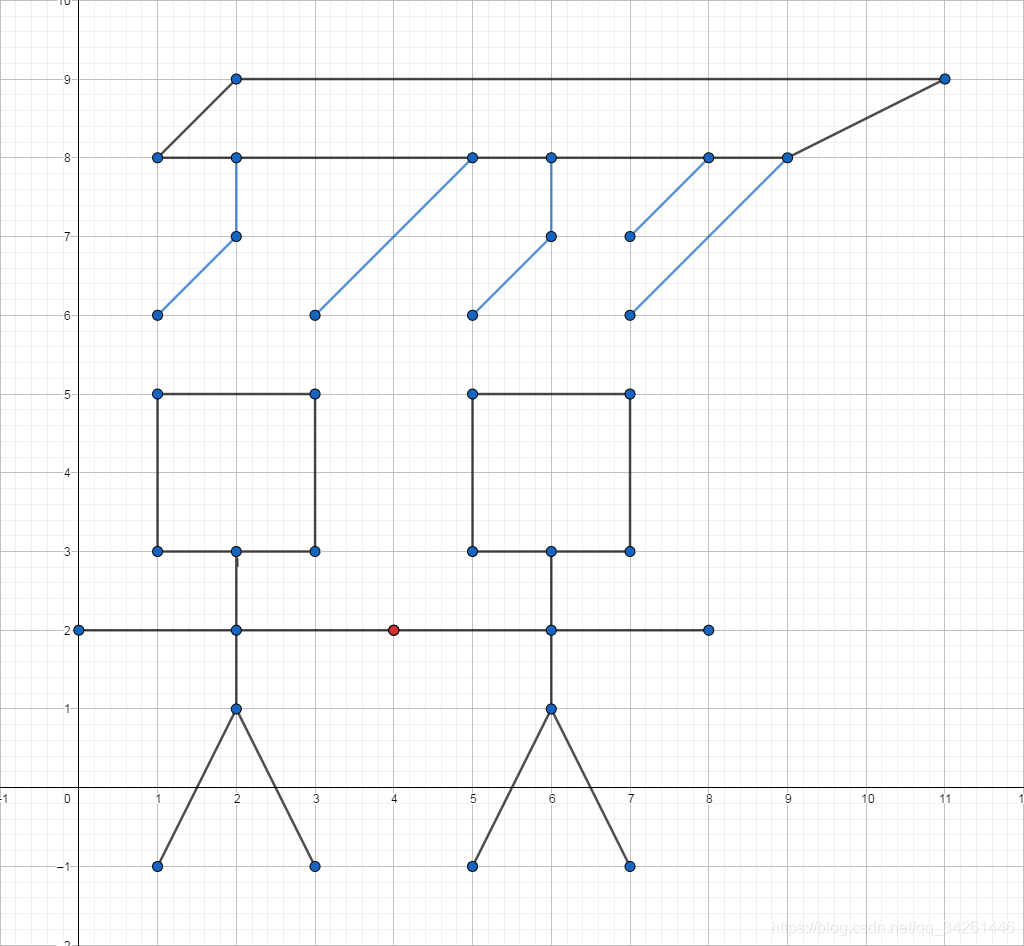
示例3
输入
复制
29
1 8 2 9
2 9 11 9
11 9 9 8
9 8 1 8
1 6 2 7
2 7 2 8
3 6 5 8
5 6 6 7
6 7 6 8
7 6 9 8
7 7 8 8
1 3 1 5
1 5 3 5
3 5 3 3
3 3 1 3
2 1 2 3
0 2 2 2
2 2 4 2
1 -1 2 1
3 -1 2 1
5 3 5 5
5 5 7 5
7 5 7 3
7 3 5 3
6 1 6 3
4 2 6 2
6 2 8 2
5 -1 6 1
7 -1 6 1
输出
复制
2

说明

思路如下

题意：题目给出 n 条直线的端点，通过每次次的祈祷，可以把其中相交的线段都去掉，问我们需要祈祷多少次才可以，把所有线段都消除，那么我们就要考虑两个问题：怎么判断直线相交、怎么一次把所有相交的直线都消去。对于前一个问题我也没看懂到大佬的题解，但对于第二个问题，我们可以明确的看出可以并查集来解决，通过判断线段相交，把所有的相交的线段视为一个集合，这样有几个集合我们就需要祈祷 几次

并查集总结传送门

题解如下（贴出大佬的代码一起共赏）

#include<set>
#include<map>
#include<cmath>
#include<ctime>
#include<queue>
#include<stack>
#include<cstdio>
#include<string>
#include<vector>
#include<cstdlib>
#include<cstring>
#include<iomanip>
#include<iostream>
#include<algorithm>
#define fi first
#define se second
#define db double
#define gcd __gcd
#define pb push_back
#define lowbit(x) (x & (-x))
#define PII  pair<int, int>
#define all(x) x.begin(), x.end()
#define debug(x) cout << #x << " = " << x << endl
#define rep(i, a, b) for(__typeof(b) i = a; i <= (b); i++)
#define Rep(i, a, b) for(__typeof(a) i = a; i >= (b); i--)
#define Mod(a,b) a<b?a:a%b+b
template<class T> inline T qmin(T a, T b) { return a < b ? a : b; }
template<class T> inline T qmax(T a, T b) { return a > b ? a : b; }
typedef long long ll;
typedef unsigned long long ull;
const db PI = acos(-1);
const int inf = 0x3f3f3f3f;
const int mod = (int)1e9 + 1;
const int maxn = (int)1e5 + 5;//remember to modify it, No RE&nbs***bsp;MLE
const ll INF = 0x3f3f3f3f3f3f3f3f;
using namespace std;
#define cross(p1, p2, p3) ((p2.x - p1.x) * (p3.y - p1.y) - (p3.x - p1.x) * (p2.y - p1.y))
#define cross0p(p1, p2, p3) sign(cross(p1,p2,p3))
const db eps = 1e-9;
inline int sign(db a) { return a < -eps ? -1: a > eps; }
inline int cmp(db a, db b) { return sign(a-b); }
struct P{
    db x, y;
    P() {}
    P(db _x, db _y): x(_x), y(_y) {}
    P operator+(P p) { return {x + p.x, y + p.y}; }
    P operator-(P p) { return {x - p.x, y - p.y}; }
    P operator*(db d) { return {x * d, y * d}; }
    P operator/(db d) { return {x / d, y / d}; }
    bool operator<(P p)const {
        int c = cmp(x, p.x);
        if(c) return c == -1;
        return cmp(y, p.y) == -1;
    }
    bool operator==(P o) const {
        return cmp(x, o.x) == 0 && cmp(y, o.y) == 0;
    }
    db distTo(P p) { return (*this - p).abs(); }
    db abs() { return sqrt(abs2()); }
    db abs2() { return x * x + y * y; }
    db dot(P p) { return x * p.x + y * p.y; }
    db det(P p) { return x * p.y - y * p.x; }
};
bool intersect(db l1, db r1, db l2, db r2)
{
    if(l1 > r1)swap(l1, r1); if(l2 > r2) swap(l2, r2);
    return !( cmp(r1, l2) == -1 || cmp(r2, l1) == -1);
}
bool isSS(P p1, P p2, P q1, P q2){
    return intersect(p1.x, p2.x, q1.x, q2.x) && intersect(p1.y, p2.y, q1.y, q2.y) && cross0p(p1, p2, q1) * cross0p(p1, p2, q2) <= 0 && cross0p(q1, q2, p1) * cross0p(q1, q2, p2) <= 0;
}
//并查集开始
int f[maxn];
int find(int x)     //递归查找x元素的父节点
{
    if(f[x] == x)
        return x;
    return f[x] = find(f[x]);   //注意这里在查找父节点的时候 已经把节点的路径进行了压缩（进行了优化）
}
void Union(int x,int y)
{
    int fx  = find(x),fy = find(y);
    if(fx != fy) f[fx] = fy;        //x,y是是有关系的，但是他们的父节点不同所以要 把其中的一个赋接待你作为子节点 拼接到临一个父节点上
}                                   //这样x、 y 就有了相同的父节点，就属于同一个集合了
int main()
{
    int n;
    P p[10005], q[10005];
    scanf("%d", &n);
    for(int i = 1 ; i <= n ; i++){
        f[i] = i;           //并查集元素的初始化
        scanf("%lf %lf %lf %lf", &p[i].x, &p[i].y, &q[i].x, &q[i].y);
    }
    for(int i = 1 ; i <= n ; i++){
        for(int j = i + 1 ; j <= n ; j++){
            if(isSS(p[i], q[i], p[j], q[j]))Union(i, j);//如果为真i，j 是有关系的，所以他们应该在同一个集合中
        }
    }
    int ans = 0;
    for(int i = 1 ; i <= n ; i++)if(f[i] == i)ans++;
    printf("%d\n", ans);
    return 0;
}