Day7 - C - Saddle Point ZOJ - 3955

Chiaki has an n × m matrix A. Rows are numbered from 1 to n from top to bottom and columns are numbered from 1 to m from left to right. The element in the i-th row and the j-th column is Ai, j.

Let M({i1, i2, ..., is}, {j1, j2, ..., jt}) be the matrix that results from deleting row i1, i2, ..., is and column j1, j2, ..., jt of A and f({i1, i2, ..., is}, {j1, j2, ..., jt}) be the number of saddle points in matrix M({i1, i2, ..., is}, {j1, j2, ..., jt}).

Chiaki would like to find all the value of f({i1, i2, ..., is}, {j1, j2, ..., jt}). As the output may be very large ((2n - 1)(2m - 1) matrix in total), she is only interested in the value

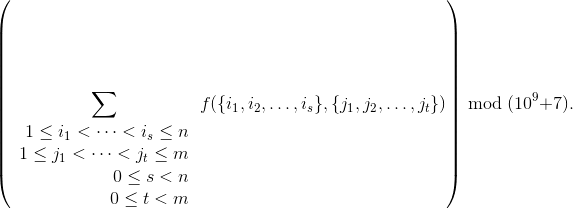
Note that a saddle point of a matrix is an element which is both the only largest element in its column and the only smallest element in its row.

Input

There are multiple test cases. The first line of input contains an integer T, indicating the number of test cases. For each test case:

The first line contains four integers n and m (1 ≤ n, m ≤ 1000) -- the number of rows and the number of columns.

Each of the next n lines contains m integer Ai, 1, Ai, 2, ..., Ai, m (1 ≤ Ai, j ≤ 106), where Ai, j is the integer in the i-th row and the j-th column.

It is guaranteed that neither the sum of all n nor the sum of all m exceeds 5000.

Output

For each test case, output an integer denoting the answer.

Sample Input

2
2 2
1 1
1 1
4 5
1 2 3 4 5
6 7 8 9 10
11 12 13 14 15
16 17 18 19 20

Sample Output

4
465

思路：saddle点的定义是行最小，列最大，那么我们就统计每一个点对saddle点的贡献，即这些点是saddle点的时候，去掉当前行比他大的列与当前列比他小的行对该点的贡献无影响，即是组合数从0到x，就是2^x，列同理，就是2^(x+y)，快速幂+二分查找即可

typedef long long LL;

const int MOD = 1e9+;
const int maxm = ;

int A[maxm][maxm], R[maxm][maxm], C[maxm][maxm];

LL quick_pow(LL a, LL b) {
    LL ret = ;
    while(b) {
        if(b & ) ret = (ret * a) % MOD;
        a = (a * a) % MOD;
        b >>= ;
    }
    return ret;
}

int main() {
    int T, n, m;
    scanf("%d", &T);
    while(T--) {
        scanf("%d%d", &n, &m);
        for(int i = ; i <= n; ++i)
            for(int j = ; j <= m; ++j) {
                scanf("%d", &A[i][j]);
                R[i][j] = C[j][i] = A[i][j];
            }
        for(int i = ; i <= n; ++i)
            sort(R[i]+, R[i]+m+);
        for(int i = ; i <= m; ++i)
            sort(C[i]+, C[i]++n);

        LL ans = ;
        int row, col;
        for(int i = ; i <= n; ++i) {
            for(int j = ; j <= m; ++j) {
                row = m-(upper_bound(R[i]+, R[i]++m, A[i][j]) - R[i] - ); // larger than A[i][j] in row
                col = lower_bound(C[j]+, C[j]++n, A[i][j]) - C[j] - ; // lower than A[i][j] in column
                ans = (ans+quick_pow(, col+row))%MOD;
            }
        }
        printf("%lld\n", ans);
    }
    return ;
}