R 对数变换 《回归分析与线性统计模型》page103

BG：在box-cox变换中，当λ = 0时即为对数变换。

当所分析变量的标准差相对于均值而言比较大时，这种变换特别有用。对数据作对数变换常常起到降低数据波动性和减少不对称性的作用。。这一变换也能有效消除异方差性

library(MASS)
library(openxlsx)
data= read.xlsx("data104.xlsx",sheet = 1) #导入数据
attach(data)

　　

op<-par(mfrow=c(2,2),mar=0.4+c(4,4,1,1),oma=c(0,0,2,0)) #将四张图放在一起，调整边界。(以后也采用此行)
plot(size,effort)            #图4-4(a)
plot(log(size),log(effort))  #图4-4(b)
#绘制频率分布直方图
hist(effort) #图4-5(a)
hist(size)   #图4-5(b)

　　

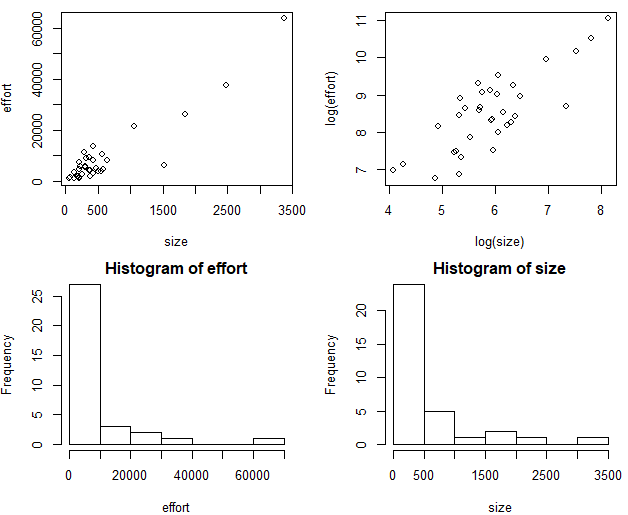
effor 和 size 这两个变量的频率分布图表明，它们并不满足正态分布。为了接近正态分布，必须变换这些变量（通过频率分布图判断变量是否满足正态分布）

1.先进行基本的线性回归，利用得到的模型进行box-cox变换

lm1=lm(effort~size+t14)  #拟合线性回归模型
summary(lm1)
#绘制残差图进行残差分析
plot(fitted(lm1),resid(lm1),cex=1.2,pch=21,col="red",bg="orange",xlab="Fitted value",ylab="Residuals")
boxcox(lm1,lambda=seq(0,1,by=0.1))  #进行box-cox变换

　　

从残差图可以看到误差项不满足Gauss-Markov假设。

右图的Box-Cox变换建议问哦们λ可以取在[0.05,0.6]范围内，对投入工作量(effort) 取对数有一定的可信度(λ=0 几乎落在置信域内)

进行对数变换

lm2=lm(log(effort)~size+t14)
summary(lm2)
#绘制残差图
plot(fitted(lm2),resid(lm2),cex=1.2,pch=21,col="red",bg="orange",xlab="Fitted value",ylab="Residuals")

　　

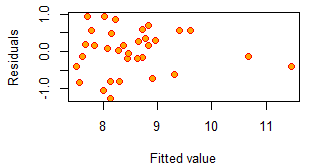
书上的结果时残差范围大致在[-25,40]内，不满足Gauss-Markov假设

与书上结果不符，上图参擦汗图表示这个模型是可行的。

2.试图拟合 effort 与 log(size)，t14 的回归方程。

lm3=lm(effort~log(size)+t14)
summary(lm3)
#绘制残差图
plot(fitted(lm3),resid(lm3),cex=1.2,pch=21,col="red",bg="orange",xlab="Fitted value",ylab="Residuals")
#box-cox变换求λ
boxcox(lm3,lambda=seq(0,1,by=0.1))

　　

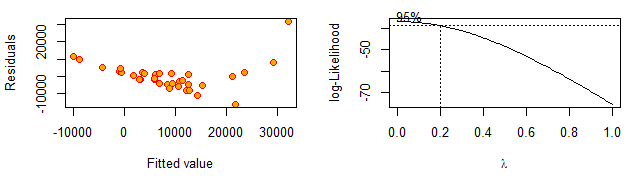
根据右图，Box-Cox变换建议我们取 λ=0

建立如下方程 ln(effort) = β0 + β1ln(size) + β2 t14 + e

lm4=lm(log(effort)~log(size)+t14) #进行线性回归
summary(lm4)
#绘制残差图
plot(fitted(lm4),resid(lm4),cex=1.2,pch=21,col="red",bg="orange",xlab="Fitted value",ylab="Residuals")
#进行box-cox变换
boxcox(lm4,lambda=seq(0,1,by=0.1))

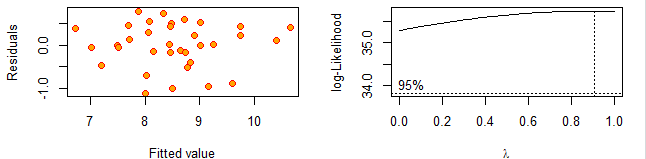
因为λ=1 包含在box-cox图像所示的置信域内，说明不进行变换也是ok的

而且通过残差分析，可以看出这个模型是合理的。