[算法]Huffman树(哈夫曼树)

---

目录

• 一、关于Huffman树
• 二、具体实现
  • 例1：P1090 合并果子
  • 例2：P2168 [NOI2015]荷马史诗

一、关于Huffman树

Huffman树(哈夫曼树)可以解决下述问题：

• 一颗\(n\)个叶节点的\(k\)叉树，第\(i\)个叶节点的权值为\(w_i\)，现在欲求\(\sum w_i\times l_i\)的最小值，其中\(l_i\)表示第\(i\)个叶子节点到根结点的距离。

二、具体实现

为了保证\(\sum w_i\times l_i\)最小，我们应该保证权值越大的叶节点深度越小。可以看出，这是很简单的贪心思想。

特殊地，我们可以先从二叉Huffman树开始研究。二叉Huffman树的实现过程如下：

1.构造一个小根堆，依次插入这\(n\)个节点的权值。

2.从堆内依次取出权值最小的两个节点\(w_1，w_2\)，令\(ans+=w_1+w_2\)。

3.把\(w_1+w_2\)作为新的节点\(w_3\)，并插入到堆中。此时\(w_3\)为\(w_1，w_2\)的父亲节点。

4.重复上述操作，直到堆的大小等于1。

Huffman树并没有真正的建立一棵树，只是在操作的时候形成一棵树的结构。

下图是二叉Huffman树的具体执行过程：最终ans=33。

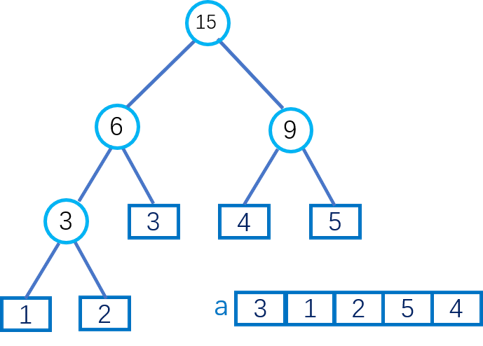
for(int i=1;i<n;i++){//n个数，操作(n-1)次
	int x=q.top();q.pop();
	int y=q.top();q.pop();
	q.push(x+y);
	ans+=x+y;
}

例1：P1090 合并果子

分析：

因为多多每次合并消耗的体力等于要合并的两堆果子的重量之和，所以最终消耗的体力就是每堆果子的重量\(\times\)合并的次数。这正符合Huffman树能解决的问题类型。

代码如下：

#include<bits/stdc++.h>
using namespace std;
priority_queue<int,vector<int>,greater<int> > q;//小根堆
int a[10010],ans;
int main()
{
	int n;
	scanf("%d",&n);
	for(int i=1;i<=n;i++){
		scanf("%d",&a[i]);
		q.push(a[i]);
	}
	while(n!=1){//重复操作直到只剩下一个节点
		int x=q.top();q.pop();
		int y=q.top();q.pop();
		q.push(x+y);
		ans+=x+y;
		n--;
	}
	printf("%d",ans);
	return 0;
}

现在我们由二叉延伸到k叉Huffman树。此时将每次取出的2个数改为k个数。这时存在一个问题，在最后一次取值时，剩余的节点可能不足以取出k个。显然这样不是最优解，当我们任取Huffman树中一个深度最大的节点，并改为树根的子节点，此时\(\sum w_i \times l_i\)就会更小。

因此只有我们补加一些额外的空节点，并将这些空节点放置在最底层时才能保证贪心算法的正确性。

当\((n-1)mod(k-1)\neq 0\)时，我们还需要补充\((k-1)-(n-1)mod(k-1)\)个节点保证等式\((n-1)mod(k-1)=0\)成立。

例2：P2168 [NOI2015]荷马史诗

分析：

这道题构造的编码方式其实就是Huffman编码，我们把单词出现的次数作为Huffman树的叶节点的权值，然后求出k叉Huffman树即可。

代码如下：

#include<bits/stdc++.h>
#define ll long long
using namespace std;
struct node{
	ll h,w;
	bool operator <(const node &other)const{
		return (w!=other.w)? w>other.w:h>other.h;
	}
};
priority_queue<node> q;
int n,k,sum;
ll t,ans;
int main()
{
	scanf("%d%d",&n,&k);
	for(int i=1;i<=n;i++){
		scanf("%lld",&t);
		q.push((node){1,t});
	}
	if((n-1)%(k-1)) sum=(k-1)-(n-1)%(k-1);
	for(int i=1;i<=sum;i++) q.push((node){1,0});
	sum+=n;
	while(sum!=1){
		ll partw=0,maxh=0;
		for(int i=1;i<=k;i++){
			node now=q.top();q.pop();
			partw+=now.w;
			maxh=max(maxh,now.h);
		}
		ans+=partw;
		q.push((node){maxh+1,partw});
		sum-=(k-1);
	}
	printf("%lld\n%lld",ans,q.top().h-1);
	return 0;
}

---