题目分享J
题意:从一棵树的树根出发,除树根外每个节点都有其能经过的最多次数与经过后会获得的价值(可能为负,最多只能领一次价值),问最终走回树根能获得的最大价值以及有无可达到此价值的多种走法(ps:一开始在树根就可以选择不走,也就是说最终价值总和不可能为负)
分析:首先给定最多经过次数为x,那么也就是说最多能从该节点x-1个儿子赶回该节点,自然想到贪心,这里我用的是优先队列,当然dp[i]表示从该节点往自己若干个儿子走完并回到i节点的价值总和的最大值,也就是任意一条以i为起点i为终点的路径上价值之和的最大值,那么不难想到dp[x]的值就是x的儿子中前x-1大的dp值之和再加上自己的价值,当然如果他的儿子中有价值是小于0,那就不需要将他加入优先队列中,然后就是处理是否有多种走法,第一种情况:考虑如果你要更新dp[x]的值,而他的一个儿子v被选中了,如果达到dp[v]的值有多种走法,那达到x的值一定也有多种走法,第二种情况:他的儿子中有多个(两个及以上)能达到同一个dp值,但由于经过次数的限定,他们中不能被全部选择,那么也会产生有多种走法,这里我采用的是记录最后一个需要被累加入dp[x]的dp[v]值并将它与优先队列中的下一个值比较,如果存在下一个值且与其相等,则代表有多种走法,第三种情况,如果该节点有一个儿子的价值为0,而且有剩余的步数来走他,那么走和不走的价值没有变化,也会产生这两种走法,所以要用一个bool数组记录节点i是否有多种走法然后讨论上述三种情况
代码:
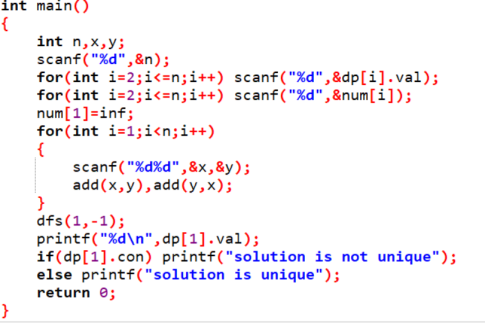
题目分享J的更多相关文章
- 20190924-LeetCode解数独题目分享
解决数独 题目描述 编写一个程序,通过已填充的空格来解决数独问题. 一个数独的解法需遵循如下规则: 数字 1-9 在每一行只能出现一次. 数字 1-9 在每一列只能出现一次. 数字 1-9 在每一个以 ...
- 题目分享E 二代目
题意:一棵点数为n的树,每个节点有点权,要求在树中中找到一个最小的x,使得存在一个点满足max(该点点权,该点相邻的点的点权+1,其他点的点权+2)=x 分析:首先要能把题目转化为上述题意 首先题目让 ...
- 题目分享D 二代目
题意:给定一个T条边的无向图,求S到E恰好经过N条边的最短路径 T≤100 N≤1000000 分析:(据说好像假期学长讲过) 首先很容易想到的是dp[i][j][k]表示从i到j经过k条边的最短路径 ...
- 题目分享C 二代目
题意:一个数列是由 1 1 2 1 2 3 1 2 3 4 1 2 3 4 5 1 2 3 4 5 6.....组成,也就是1-1,1-2,1-3......并且如果遇到多位数也要拆成数字比如1-10 ...
- 2019年腾讯PHP程序员面试题目分享
有需要学习交流的友人请加入交流群的咱们一起,有问题一起交流,一起进步!前提是你是学技术的.感谢阅读! 点此加入该群jq.qq.com 1. php 的垃圾回收机制 PHP 可以自动进行内存管理,清除 ...
- 题目分享H 二代目
题意:有m个限制,每个限制l1,r1,l2,r2四个数,限制了一个长度为n的数第l1到r1位要与第l2到r2相同,保证r1-l1=r2-l2,求在限制下一共有多少种数 分析: 暴力的话肯定是从l1-r ...
- 题目分享X
题意:一张票有n位数,如果这张票的前一半数字的和等于后一半数字的和(n一定是偶数),就称这张票为快乐票.有些数被擦除了,标记为’?’(’?‘的个数也是偶数),现在Monocarp 和 Bicarp 进 ...
- 题目分享V
题意:现在两个人做游戏,每个人刚开始都是数字1,谁赢了就能乘以k^2,输的乘以k(k可以是任意整数,每次不一定相同)现在给你最终这两个人的得分,让你判断是否有这个可能,有可能的话Yes,否则No. 分 ...
- 题目分享T
题意:蛐蛐国里现在共有n只蚯蚓(n为正整数).每只蚯蚓拥有长度,我们设第i只蚯蚓的长度为a_i(i=1,2,...,n),并保证所有的长度都是非负整数(即:可 能存在长度为0的蚯蚓).每一秒,神刀手会 ...
随机推荐
- 7.3 java 成员变量和局部变量区别
/* * 成员变量和局部变量的区别: * A:在类中的位置不同 * 成员变量:类中,方法外 * 局部变量:方法中或者方法声明上(形式参数) * B:在内存中的位置不同 * 成员变量:堆内存 * 局部变 ...
- springboot web项目创建及自动配置分析(thymeleaf+flyway)
@ 目录 源码分析 webjars thymeleaf thymeleaf语法 springmvc 启动配置原理 集成flyway插件 springboot 创建web项目只需要引入对应的web-st ...
- bat批处理文件搞定所有系统问题
bat批处理文件搞定所有系统问题 分类: WINDOWS -----------bat批处理文件搞定所有系统问题--------- 一.查漏补缺——给系统功能添把火 我们的操作系统虽然功 ...
- 使用d3.js的时候,如何用zoom translate scale限制拖拽范围
红色代表需要改写的代码 1.添加定义图像大小和容器的大小及坐标 d3.behavior.zoom = function () { var moveCanvas={ width: , height: , ...
- matlab计算LZ复杂度
我这个计算得14通道,每个通道截取3000个数据得复杂度,最后将计算得出得数据存储到本地txt文档中 function LZC(data) % 计算一维信号的复杂度 % data时间序列 % lzc: ...
- 干货:python面对对象类继承简介
前言 文的文字及图片来源于网络,仅供学习.交流使用,不具有任何商业用途,版权归原作者所有,如有问题请及时联系我们以作处理. 作者:python视觉算法 PS:如有需要Python学习资料的小伙伴可以加 ...
- 经典算法之归并排序——python和JS实现
前言 文的文字及图片来源于网络,仅供学习.交流使用,不具有任何商业用途,版权归原作者所有,如有问题请及时联系我们以作处理. 作者:韩忠康 PS:如有需要Python学习资料的小伙伴可以加点击下方链接自 ...
- stand up meeting 1/18/2016
part 组员 工作 工作耗时/h 明日计划 工作耗时/h UI 冯晓云 准备最后的发布和整个开发的整理总结 6 release ...
- E1. Send Boxes to Alice (Easy Version)
题解: 保存每个1的位置.然后记录1的总个数cnt,如果存在一个k使得这个k是每个集合的倍数,那么为了使操作次数最小,这个k应该是cnt的质因子.(因为都是每个集合的数目1,使每个集合的数目变为2需要 ...
- 百度关键词搜索工具 v1.1|url采集工具 v1.1
功能介绍:关键词搜索工具 批量关键词自动搜索采集 自动去除垃圾二级泛解析域名 可设置是否保存域名或者url 持续更新中
