Day3-C-Radar Installation POJ1328
We use Cartesian coordinate system, defining the coasting is the x-axis. The sea side is above x-axis, and the land side below. Given the position of each island in the sea, and given the distance of the coverage of the radar installation, your task is to write a program to find the minimal number of radar installations to cover all the islands. Note that the position of an island is represented by its x-y coordinates.
Figure A Sample Input of Radar Installations
Input
The input is terminated by a line containing pair of zeros
Output
Sample Input
3 2
1 2
-3 1
2 1 1 2
0 2 0 0
Sample Output
Case 1: 2
Case 2: 1 简述:每个island与X轴都有最多2个交点,求最少点满足与所有区间相交
思路:区间选点问题,将每个区间右边递增排序后寻找即可,代码如下:
#define sqr(x) ((x)*(x))
const int maxm = ;
struct Node {
double l, r;
bool operator< (const Node &a) const {
return r < a.r;
}
} Nodes[maxm];
int d, n, sum, kase = ;
int main() {
while(scanf("%d%d", &n, &d) && n) {
printf("Case %d: ", ++kase);
bool flag = true;
sum = ;
for (int i = ; i < n; ++i) {
double tx, ty, tmp;
scanf("%lf%lf", &tx, &ty); //x = tx -+ sqrt(d^2 - y0 ^2 )
if(d < ty) {
flag = false;
sum = -;
}
tmp = sqrt(sqr(d) - sqr(ty));
Nodes[i].l = tx - tmp, Nodes[i].r = tx + tmp;
}
if(flag) {
sort(Nodes, Nodes + n);
double maxr = Nodes[].r;
for (int i = ; i < n; ++i) {
if(maxr < Nodes[i].l) {
maxr = Nodes[i].r;
++sum;
}
}
}
printf("%d\n", sum);
}
return ;
}
注意在判断ty>d的时候不能提前退出,要读取完
补:
在区间选点问题上,要右端点进行排序,因为要找一个现有区间的公共点,若是左端点,会出现漏解的情况,例如:
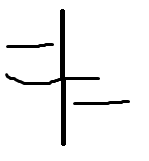
Day3-C-Radar Installation POJ1328的更多相关文章
- [POJ1328]Radar Installation
[POJ1328]Radar Installation 试题描述 Assume the coasting is an infinite straight line. Land is in one si ...
- POJ1328——Radar Installation
Radar Installation Description Assume the coasting is an infinite straight line. Land is in one side ...
- POJ--1328 Radar Installation(贪心 排序)
题目:Radar Installation 对于x轴上方的每个建筑 可以计算出x轴上一段区间可以包含这个点 所以就转化成 有多少个区间可以涵盖这所有的点 排序之后贪心一下就ok 用cin 好像一直t看 ...
- POJ1328 Radar Installation 【贪心·区间选点】
Radar Installation Time Limit: 1000MS Memory Limit: 10000K Total Submissions: 54593 Accepted: 12 ...
- 【贪心】「poj1328」Radar Installation
建模:二维转一维:贪心 Description Assume the coasting is an infinite straight line. Land is in one side of coa ...
- POJ1328 Radar Installation 解题报告
Description Assume the coasting is an infinite straight line. Land is in one side of coasting, sea i ...
- POJ 1328 Radar Installation 贪心 A
POJ 1328 Radar Installation https://vjudge.net/problem/POJ-1328 题目: Assume the coasting is an infini ...
- Radar Installation
Radar Installation 题目链接:http://acm.hust.edu.cn/vjudge/contest/view.action?cid=86640#problem/C 题目: De ...
- Radar Installation(贪心)
Radar Installation Time Limit: 1000MS Memory Limit: 10000K Total Submissions: 56826 Accepted: 12 ...
- 贪心 POJ 1328 Radar Installation
题目地址:http://poj.org/problem?id=1328 /* 贪心 (转载)题意:有一条海岸线,在海岸线上方是大海,海中有一些岛屿, 这些岛的位置已知,海岸线上有雷达,雷达的覆盖半径知 ...
随机推荐
- ROS机器人系统学习——踩坑之路
推荐学习教程:深蓝学院 机器人操作系统ROS理论与实践学习 在学习到第2讲ROS基础的分布式通信时,一直卡在这里,主机开启小海龟后,从机虽然可以通过 rostopic list 列出当前的所有topi ...
- Nexus 3048的NX-OS升级方法
1.System Software和Kick Start 与普通IOS设备不同,NX OS升级时,共有2个文件需要升级.安装,如果只安装其中一个,可能会导致设备重启后无法进入系统.这2个文件包括: N ...
- SqlServer游标操作
CLOSE orderNum_02_cursordeallocate orderNum_02_cursorDECLARE orderNum_02_cursor cursor SCROLL for se ...
- iOS 混合开发之 Cordova 实践
在15年时,之前公司使用 Cordova 做混合开发使用,后来公司没有用到了,现在重新记录下. Cordova (官网:http://cordova.apache.org/)简介: Apache Co ...
- 关于PGSQL连接问题
今天把运维管理服务移植在Linux下测试,但又不想在Linux中安装PGSQL的服务器,就想让运维管理服务在虚拟机中连接windows的PG服务,却发现PG服务器一直拒绝连接,检查了网络端口之后都没问 ...
- Redis数据的导出和导入(dump和load方式)
迁移redis数据一般有如下3种方式: 第三方工具redis-dump,redis-load aof机制,需要开启aof功能 rdb存储机制 这里介绍第一种方式,通过redis-dump导出数据,再通 ...
- 最全Pycharm教程(39)——Pycharm版本控制之本地Git用法
1.主题 介绍如果通过Pycharm使用本地Git集. 2.准备工作 (1)PyCharm版本为2.7或更高 (2)已经创建一个工程 (3)Git插件可用,对应可执行文件在 Git page页面正确配 ...
- Python3.5学习之旅——day3
本节内容: 1.字符串操作 2.字典操作 3.集合 4.文件操作 5.字符编码与转码 6.函数与函数式编程 一.字符串操作 name='kobe' name.capitalize() 首字母大写 na ...
- Hosts工作原理及作用
Hosts是一个没有扩展名的系统文件,可以用记事本等工具打开.其作用就是将一些常用的网址域名与其对应的IP地址建立一个关联“数据库”.当用户在浏览器中输入一个需要登录的网址时,系统会先检查系自己的Ho ...
- 如何去掉Eclipse注释中英文单词的拼写错误检查
