损失函数coding

损失函数(Loss Function)和成本函数(Cost Function)之间有什么区别？

在此强调这一点，尽管成本函数和损失函数是同义词并且可以互换使用，但它们是不同的。

损失函数用于单个训练样本。它有时也称为误差函数(error function)。另一方面，成本函数是整个训练数据集的平均损失(average function)。优化策略旨在最小化成本函数。

1.平方误差损失

每个训练样本的平方误差损失(也称为L2 Loss)是实际值和预测值之差的平方：（y-f(x)）^2  

相应的成本函数是这些平方误差的平均值(MSE)

import numpy as np

def update_weights_MSE(m,X, Y, learning_rate):
m_deriv = 0
b_deriv = 0
N = len(X)
for i in range(N):  #所有样本更新的权重
# 计算偏导数为
# -2x(y - (mx + b))
k = Y[i]-np.matmul(m,X[i])
m_deriv += -2*X[i] *k
# -2(y - (mx + b))
b_deriv += -2*(Y[i] - (m*X[i]))
# 我们减去它，因为导数指向最陡的上升方向
#print(m_deriv)
m = m-(m_deriv/N) * learning_rate#所有样本更新权重的均值作为整体的更新
b -= (b_deriv / float(N)) * learning_rate

return m
X = np.array([[1,2],[3,1],[0,3]])
Y = np.array([2,4,7])
m=np.array([2,3])
t = update_weights_MSE(m,X, Y, 0.1)
print(t)

把一个比较大的数平方会使它变得更大。但有一点需要注意，这个属性使MSE成本函数对异常值的健壮性降低。因此，如果我们的数据容易出现许多的异常值，则不应使用这个它。

2.绝对误差损失

L（x）=|y-f(x)|   成本是这些绝对误差的平均值(MAE).

def update_weights_MAE(m, b, X, Y, learning_rate):
    m_deriv = 0
    b_deriv = 0
    N = len(X)
    for i in range(N):
        #计算偏导数
        # -x(y - (mx + b))    可以分开写
        m_deriv += - X[i] * (Y[i] - (m*X[i] + b)) / abs(Y[i] - (m*X[i] + b))
        # -(y - (mx + b)) / |mx + b|
        b_deriv += -(Y[i] - (m*X[i] + b)) / abs(Y[i] - (m*X[i] + b))
    #我们减去它，因为导数指向最陡的上升方向
    m -= (m_deriv / float(N)) * learning_rate
    b -= (b_deriv / float(N)) * learning_rate
    return m, b

3.Huber损失

Huber损失结合了MSE和MAE的最佳特性。对于较小的误差，它是二次的，否则是线性的(对于其梯度也是如此)。Huber损失需要确定δ参数

def update_weights_Huber(m, b, X, Y, delta, learning_rate):
    m_deriv = 0
    b_deriv = 0
    N = len(X)
    for i in range(N):
        # 小值的二次导数，大值的线性导数
        if abs(Y[i] - m*X[i] - b) <= delta:
            m_deriv += -X[i] * (Y[i] - (m*X[i] + b))
            b_deriv += - (Y[i] - (m*X[i] + b))
        else:
            m_deriv += delta * X[i] * ((m*X[i] + b) - Y[i]) / abs((m*X[i] + b) - Y[i])
            b_deriv += delta * ((m*X[i] + b) - Y[i]) / abs((m*X[i] + b) - Y[i])
    #我们减去它，因为导数指向最陡的上升方向
    m -= (m_deriv / float(N)) * learning_rate
    b -= (b_deriv / float(N)) * learning_rate
    return m, b

Huber损失对于异常值比MSE更强。它用于稳健回归(robust regression)，M估计法(M-estimator)和可加模型(additive model)。Huber损失的变体也可以用于分类。

二分类损失函数

意义如其名。二分类是指将物品分配到两个类中的一个。该分类基于应用于输入特征向量的规则。二分类的例子例如，根据邮件的主题将电子邮件分类为垃圾邮件或非垃圾邮件。

我将在乳腺癌数据集^2上说明这些二分类损失函数。
我们希望根据平均半径，面积，周长等特征将肿瘤分类为"恶性(Malignant)"或"良性(Benign)"。为简化起见，我们将仅使用两个输入特征(X_1和X_2)，即"最差区域(worst area)"和"平均对称性(mean symmetry)"用于分类。Y是二值的，为0(恶性)或1(良性)。

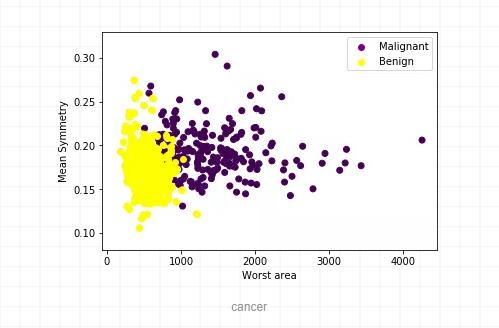
1.二元交叉熵损失

让我们从理解术语"熵"开始。通常，我们使用熵来表示无序或不确定性。测量具有概率分布p(X)的随机变量X：

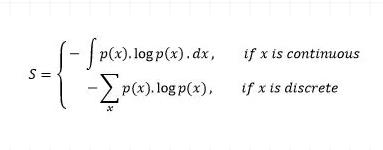
负号用于使最后的结果为正数。

概率分布的熵值越大，表明分布的不确定性越大。同样，一个较小的值代表一个更确定的分布。

这使得二元交叉熵适合作为损失函数(你希望最小化其值)。我们对输出概率p的分类模型使用二元交叉熵损失

元素属于第1类(或正类)的概率=p
元素属于第0类(或负类)的概率=1-p

然后，输出标签y(可以取值0和1)的交叉熵损失和和预测概率p定义为：

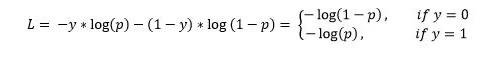
这也称为Log-Loss(对数损失)。为了计算概率p，我们可以使用sigmoid函数。这里，z是我们输入功能的函数

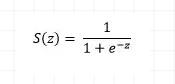
sigmoid函数的范围是[0,1]，这使得它适合于计算概率。

def update_weights_BCE(m1, m2, b, X1, X2, Y, learning_rate):
    m1_deriv = 0
    m2_deriv = 0
    b_deriv = 0
    N = len(X1)
    for i in range(N):
        s = 1 / (1 / (1 + math.exp(-m1*X1[i] - m2*X2[i] - b)))
        # 计算偏导数
        m1_deriv += -X1[i] * (s - Y[i])
        m2_deriv += -X2[i] * (s - Y[i])
        b_deriv += -(s - Y[i])
    # 我们减去它，因为导数指向最陡的上升方向
    m1 -= (m1_deriv / float(N)) * learning_rate
    m2 -= (m2_deriv / float(N)) * learning_rate
    b -= (b_deriv / float(N)) * learning_rate
    return m1, m2, b

2.Hinge损失

Hinge损失主要用于带有类标签-1和1的支持向量机(SVM)。因此，请确保将数据集中"恶性"类的标签从0更改为-1。

Hinge损失不仅会惩罚错误的预测，还会惩罚不自信的正确预测

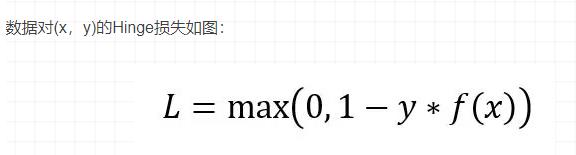
def update_weights_Hinge(m1, m2, b, X1, X2, Y, learning_rate):

m1_deriv = 0
    m2_deriv = 0
    b_deriv = 0
    N = len(X1)
    for i in range(N):
        # 计算偏导数
        if Y[i]*(m1*X1[i] + m2*X2[i] + b) <= 1:
            m1_deriv += -X1[i] * Y[i]
            m2_deriv += -X2[i] * Y[i]
            b_deriv += -Y[i]
        # 否则偏导数为0
    # 我们减去它，因为导数指向最陡的上升方向
    m1 -= (m1_deriv / float(N)) * learning_rate
    m2 -= (m2_deriv / float(N)) * learning_rate
    b -= (b_deriv / float(N)) * learning_rate
return m1, m2, b

Hinge损失简化了SVM的数学运算，同时最大化了损失(与对数损失(Log-Loss)相比)。当我们想要做实时决策而不是高度关注准确性时，就可以使用它。

多分类损失函数详见softmax