DQN（Deep Q-learning）入门教程（四）之Q-learning Play Flappy Bird

在上一篇博客中，我们详细的对Q-learning的算法流程进行了介绍。同时我们使用了$\epsilon-贪婪法$防止陷入局部最优。

那么我们可以想一下，最后我们得到的结果是什么样的呢？因为我们考虑到了所有的（$\epsilon-贪婪法$导致的）情况，因此最终我们将会得到一张如下的Q-Table表。

Q-Table	$a_1$	$a_2$
$s_1$	$q(s_1,a_1)$	$q(s_1,a_2)$
$s_2$	$q(s_2,a_1)$	$q(s_2,a_2)$
$s_3$	$q(s_3,a_1)$	$q(s_3,a_2)$

当agent运行到某一个场景$s$时，会去查询已经训练好的Q-Table，然后从中选择一个最大的$q$对应的action。

训练内容

这一次，我们将对Flappy-bird游戏进行训练。这个游戏的介绍我就不多说了，可以看一下维基百科的介绍。

游戏就是控制一只穿越管道，然后可以获得分数，对于小鸟来说，他只有两个动作，跳or不跳，而我们的目标就是使小鸟穿越管道获得更多的分数。

前置准备

因为我们的目标是来学习“强化学习”的，所以我们不可能说自己去弄一个Flappy-bird（当然自己弄也可以），这里我们直接使用一个已经写好的Flappy-bird。

PyGame-Learning-Environment，是一个Python的强化学习环境，简称PLE，下面时他Github上面的介绍：

PyGame Learning Environment (PLE) is a learning environment, mimicking the Arcade Learning Environment interface, allowing a quick start to Reinforcement Learning in Python. The goal of PLE is allow practitioners to focus design of models and experiments instead of environment design.

PLE hopes to eventually build an expansive library of games.

然后关于FlappyBird的文档介绍在这里，文档的介绍还是蛮清楚的。安装步骤如下所示，推荐在Pipenv的环境下安装，不过你也可以直接clone我的代码然后然后根据reademe的步骤进行使用。

git clone https://github.com/ntasfi/PyGame-Learning-Environment.git

cd PyGame-Learning-Environment/

pip install -e .

需要的库如下：

pygame
numpy
pillow

函数说明

在官方文档有几个的函数在这里说下，因为等下我们需要用到。

getGameState()：获得游戏当前的状态，返回值为一个字典：
1. player y position.
2. players velocity.
3. next pipe distance to player
4. next pipe top y position
5. next pipe bottom y position
6. next next pipe distance to player
7. next next pipe top y position
8. next next pipe bottom y position
部分数据表示如下：
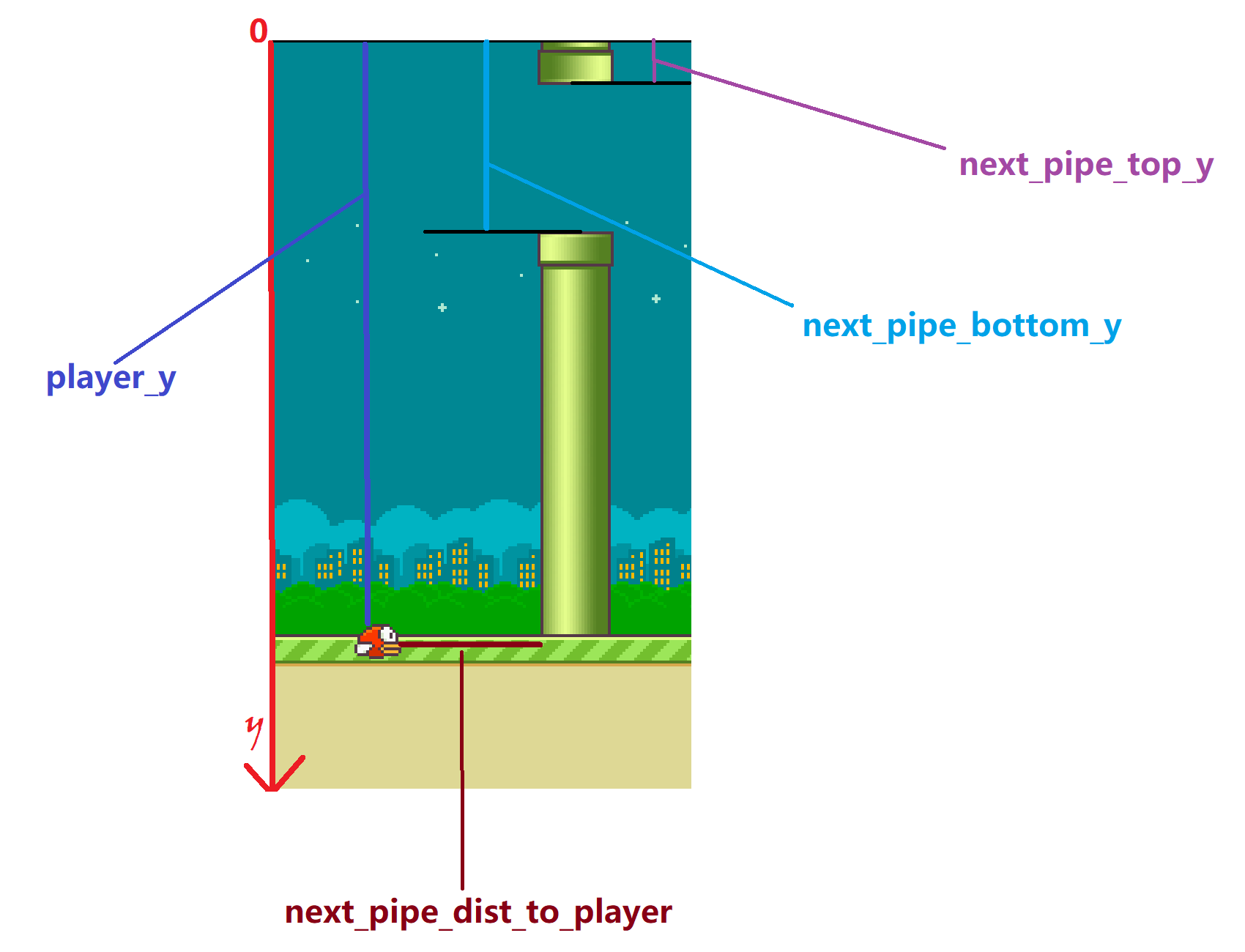
reset_game()：重新开始游戏
act(action)：在游戏中执行一个动作，参数为动作，返回执行后的分数。
game_over()：假如游戏结束，则返回True，否者返回False。
getActionSet()：获得游戏的动作集合。

我们的窗体大小默认是288*512，其中鸟的速度在-20到10之间（最小速度我并不知道，但是经过观察，并没有小于-20的情况，而最大的速度在源代码里面已经说明好了为10）

Coding Time

在前面我们说，通过getGameState()函数，我们可以获得几个关于环境的数据，在这里我们选择如下的数据：

next_pipe_dist_to_player：
player_y与next_pipe_top_y的差值
的速度

但是我们可以想一想，next_pipe_dist_to_player一共会有多少种的取值：因为窗体大小为288*512，则取值的范围大约是0~288，也就是说它大约有288个取值，而关于player_y与next_pipe_top_y的差值，则大概有1024个取值。这样很难让模型收敛，因此我们将数值进行简化。其中简化的思路来自：GitHub

首先我们创建一个Agent类，然后逐渐向里面添加功能。

class Agent():

    def __init__(self, action_space):

        # 获得游戏支持的动作集合

        self.action_set = action_space

        # 创建q-table

        self.q_table = np.zeros((6, 6, 6, 2))

        # 学习率

        self.alpha = 0.7

        # 励衰减因子

        self.gamma = 0.8

        # 贪婪率

        self.greedy = 0.8

至于为什么q-table的大小是(6,6,6,2)，其中的3个6分别代表next_pipe_dist_to_player，player_y与next_pipe_top_y的差值，的速度，其中的2代表动作的个数。也就是说，表格中的state一共有$6 \times6 \times 6 $种，表格的大小为$6 \times6 \times 6 \times 2$。

缩小状态值的范围

我们定义一个函数get_state(s)，这个函数专门提取游戏中的状态，然后返回进行简化的状态数据：

    def get_state(self, state):

        """

        提取游戏state中我们需要的数据

        :param state: 游戏state

        :return: 返回提取好的数据

        """

        return_state = np.zeros((3,), dtype=int)

        dist_to_pipe_horz = state["next_pipe_dist_to_player"]

        dist_to_pipe_bottom = state["player_y"] - state["next_pipe_top_y"]

        velocity = state['player_vel']

        if velocity < -15:

            velocity_category = 0

        elif velocity < -10:

            velocity_category = 1

        elif velocity < -5:

            velocity_category = 2

        elif velocity < 0:

            velocity_category = 3

        elif velocity < 5:

            velocity_category = 4

        else:

            velocity_category = 5

        if dist_to_pipe_bottom < 8:  # very close or less than 0

            height_category = 0

        elif dist_to_pipe_bottom < 20:  # close

            height_category = 1

        elif dist_to_pipe_bottom < 50:  # not close

            height_category = 2

        elif dist_to_pipe_bottom < 125:  # mid

            height_category = 3

        elif dist_to_pipe_bottom < 250:  # far

            height_category = 4

        else:

            height_category = 5

        # make a distance category

        if dist_to_pipe_horz < 8:  # very close

            dist_category = 0

        elif dist_to_pipe_horz < 20:  # close

            dist_category = 1

        elif dist_to_pipe_horz < 50:  # not close

            dist_category = 2

        elif dist_to_pipe_horz < 125:  # mid

            dist_category = 3

        elif dist_to_pipe_horz < 250:  # far

            dist_category = 4

        else:

            dist_category = 5

        return_state[0] = height_category

        return_state[1] = dist_category

        return_state[2] = velocity_category

        return return_state

更新Q-table

更新的数学公式如下：

\[{\displaystyle Q^{new}(s_{t},a_{t})\leftarrow \underbrace {Q(s_{t},a_{t})} _{\text{旧的值}}+\underbrace {\alpha } _{\text{学习率}}\cdot \overbrace {{\bigg (}\underbrace {\underbrace {r_{t}} _{\text{奖励}}+\underbrace {\gamma } _{\text{奖励衰减因子}}\cdot \underbrace {\max _{a}Q(s_{t+1},a)} _{\text{estimate of optimal future value}}} _{\text{new value (temporal difference target)}}-\underbrace {Q(s_{t},a_{t})} _{\text{旧的值}}{\bigg )}} ^{\text{temporal difference}}}
\]

下面是更新Q-table的函数代码：

def update_q_table(self, old_state, current_action, next_state, r):

    """

    :param old_state: 执行动作前的状态

    :param current_action: 执行的动作

    :param next_state: 执行动作后的状态

    :param r: 奖励

    :return:

    """

    next_max_value = np.max(self.q_table[next_state[0], next_state[1], next_state[2]])

    self.q_table[old_state[0], old_state[1], old_state[2], current_action] = (1 - self.alpha) * self.q_table[

        old_state[0], old_state[1], old_state[2], current_action] + self.alpha * (r + next_max_value)

选择最佳的动作

然后我们就是根据q-table对应的Q值选择最大的那一个，其中第一个代表（也就是0）跳跃，第2个代表不执行任何操作。

选择的示意图如下：

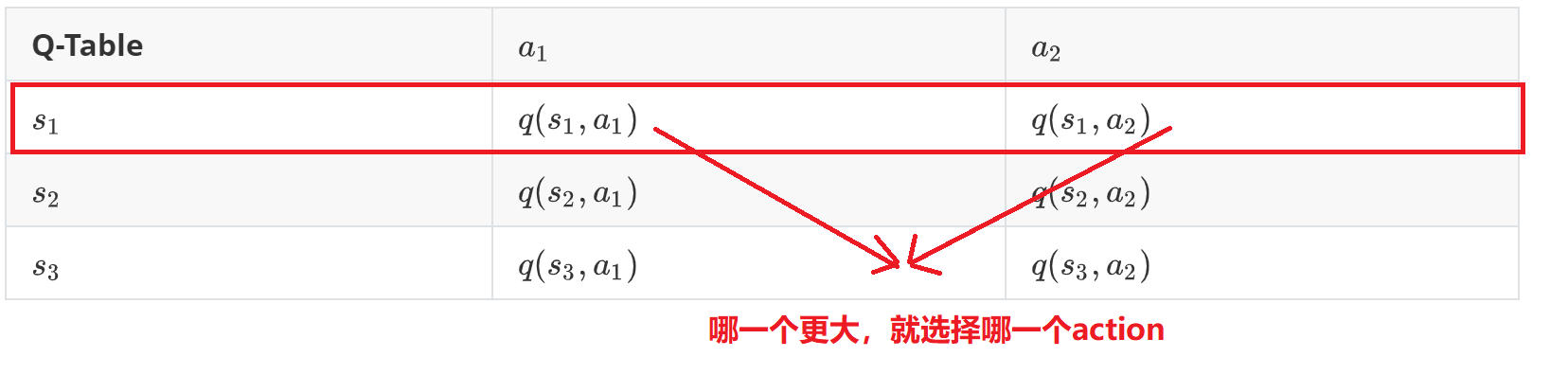
代码如下所示：

def get_best_action(self, state, greedy=False):

    """

    获得最佳的动作

    :param state: 状态

    :是否使用ϵ-贪婪法

    :return: 最佳动作

    """

    # 获得q值

    jump = self.q_table[state[0], state[1], state[2], 0]

    no_jump = self.q_table[state[0], state[1], state[2], 1]

    # 是否执行策略

    if greedy:

        if np.random.rand(1) < self.greedy:

            return np.random.choice([0, 1])

        else:

            if jump > no_jump:

                return 0

            else:

                return 1

    else:

        if jump > no_jump:

            return 0

        else:

            return 1

更新$\epsilon$值

这个比较简单，从前面的博客中，我们知道$\epsilon$是随着训练次数的增加而减少的，有很多种策略可以选择，这里乘以$0.95$吧。

def update_greedy(self):

    self.greedy *= 0.95

执行动作

在官方文档中，如果小鸟没有死亡奖励为0，越过一个管道，奖励为1，死亡奖励为-1，我们稍微的对其进行改变：

def act(self, p, action):

    """

    执行动作

    :param p: 通过p来向游戏发出动作命令

    :param action: 动作

    :return: 奖励

    """

    # action_set表示游戏动作集(119，None)，其中119代表跳跃

    r = p.act(self.action_set[action])

    if r == 0:

        r = 1

    if r == 1:

        r = 10

    else:

        r = -1000

    return r

main函数

最后我们就可以执行main函数了。

if __name__ == "__main__":

    # 训练次数

    episodes = 2000_000000

    # 实例化游戏对象

    game = FlappyBird()

    # 类似游戏的一个接口，可以为我们提供一些功能

    p = PLE(game, fps=30, display_screen=False)

    # 初始化

    p.init()

    # 实例化Agent，将动作集传进去

    agent = Agent(p.getActionSet())

    max_score = 0

    for episode in range(episodes):

        # 重置游戏

        p.reset_game()

        # 获得状态

        state = agent.get_state(game.getGameState())

        agent.update_greedy()

        while True:

            # 获得最佳动作

            action = agent.get_best_action(state)

            # 然后执行动作获得奖励

            reward = agent.act(p, action)

            # 获得执行动作之后的状态

            next_state = agent.get_state(game.getGameState())

            # 更新q-table

            agent.update_q_table(state, action, next_state, reward)

            # 获得当前分数

            current_score = p.score()

            state = next_state

            if p.game_over():

                max_score = max(current_score, max_score)

                print('Episodes: %s, Current score: %s, Max score: %s' % (episode, current_score, max_score))

                # 保存q-table

                if current_score > 300:

                    np.save("{}_{}.npy".format(current_score, episode), agent.q_table)

                break

部分的训练的结果如下：

总结

emm，说实话，我也不知道结果会怎么样，因为训练的时间比较长，我不想放在我的电脑上面跑，然后我就放在树莓派上面跑，但是树莓派性能比较低，导致训练的速度比较慢。但是，我还是觉得我的方法有点问题，get_state()函数中简化的方法，我感觉不是特别的合理，如果各位有好的看法，可以在评论区留言哦，然后共同学习。

项目地址：https://github.com/xiaohuiduan/flappy-bird-q-learning

参考