Quoted-printable 编码介绍、编码解码转换

求教，“=B9=A4=D7=F7=BC=F2=B1=A8” 这种是什么编码方式？

Quoted-printable 可译为“可打印字符引用编码”、“使用可打印字符的编码”，我们收邮件，查看信件原始信息，经常会看到这种类型的编码！

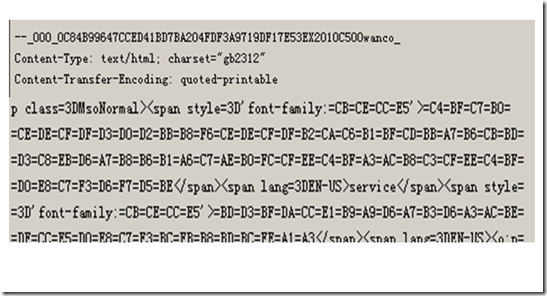
最多时候，我们在邮件头里面能够看到这样的编码！Content-Transfer-Encoding:quoted-printable

它是多用途互联网邮件扩展（MIME) 一种实现方式。其中MIME是一个互联网标准，它扩展了电子邮件标准，致力于使其能够支持非ASCII字符、二进制格式附件等多种格式的邮件消息。目前http协议中，很多采用MIME框架！quoted-printable 就是说用一些可打印常用字符，表示一个字节（8位）中所有非打印字符方法！

Quoted-printable编码方法

任何一个8位的字节值可编码为3个字符：一个等号”=”后跟随两个十六进制数字(0–9或A–F)表示该字节的数值.例如，ASCII码换页符（十进制值为12）可以表示为”=0C”, 等号”=”（十进制值为61）必须表示为”=3D”. 除了可打印ASCII字符与换行符以外，所有字符必须表示为这种格式.

所有可打印ASCII字符(十进制值的范围为33到126)可用ASCII字符编码来直接表示, 但是等号”=”(十进制值为61)不可以这样直接表示.ASCII的水平制表符(tab)与空格符, 十进制为9和32, 如果不出现在行尾则可以用其ASCII字符编码直接表示。如果这两个字符出现在行尾，必须QP编码表示为”=09″ (tab)或”=20″ (space).

如果数据中包含有意义的行结束标志，必须转换为ASCII回车(CR)换行(LF)序列，既不能用原来的ASCII字符也不能用QP编码的”=”转义字符序列。 相反，如果字节值13与10有其它的不是行结束的含义，它们必须QP编码为=0D与=0A.

quoted-printable编码的数据的每行长度不能超过76个字符. 为满足此要求又不改变被编码文本，在QP编码结果的每行末尾加上软换行(soft line break). 即在每行末尾加上一个”=”, 但并不会出现在解码得到的文本中.

例如：If you believe that truth=beauty, then surely mathematics is the most beautiful branch of philosophy. 编码后结果是

If you believe that truth=3Dbeauty, then surely=20=
mathematics is the most beautiful branch of philosophy.

编码里面，有几个特定限定，一些可打印字符不用编码，当然如果你按照规范编码后，也一样可以显示的！因此自己简单自己实现该编码:

function quoted_printable_encode($string) { 
    return preg_replace('/[^\r\n]{73}[^=\r\n]{2}/', "$0=\r\n", str_replace("%","=",
rawurlencode($string))); 
} 

一个函数就可以，将所有字符串urlencode转换后，%号替换为”=”号，然后对非\r\n超过73连续字符，后面加一个=\r\n。这个是简单实现方法！ 按照该编码详细说明里面，有些空格、换行，还有一些特殊字符可以不用转换。不过一起转换了，也不会有影响！

很多时候，我们用些常见字符表示所有8位其它非打印字符，这种通过，Quoted-printable编码，只是对该字节转为16进制后，做简单增加前缀！然后做些特殊字符处理即可！ 它的简单，及编码高效，也让该编码在邮件格式里面，得到了广泛使用！好了，就到这里，欢迎交流！

暂无相关文章！

原文网址：http://blog.chacuo.net/494.html