HDU 2686 (双线程) Matrix

这也是当初卡了很久的一道题

题意：从左上角的格子出发选一条路径到右上角然后再回到左上角，而且两条路径除了起点和终点不能有重合的点。问所经过的格子中的最大和是多少

状态设计：我们可以认为是从左上角出发了两条路径，然后同时到达右下角。容易看出，第k个阶段所有可能到达的格子构成一条斜线而且满足x1 + y1 = x2 + y2 = k + 1

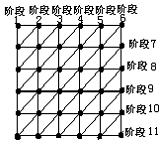
dp[k][x1][x2]表示第k阶段两条路分别到达(x1, y1) (x2, y2)所能取得的最大值(y1 y2根据上面的等量关系来计算)，如果x1 = x2表示两条路径汇合于一点了

状态转移方程：

在求解第k阶段最优解时，首先枚举k-1阶段时的状态(x1', x2')，然后向四个方向延伸出(x1, x2)

dp[k][x1][x2] = max{dp[k-1][x1'][x2'] + num[x1][y1] | (x1=x2),  dp[k-1][x1'][x2'] + num[x1][y1] + num[x2][y2] | (x1≠x2)}

在循环的过程中可能会出现从一个点延伸的下一个点的情况，即两条路径可能重合，不过不要紧，因为格子里面都是正数，所以得到的最优解一定是两条不重合的路径

优化：

因为两条路径具有任意性，所以不妨规定第一条路在第二条路的下方(或同一水平线)，时间从92MS优化到62MS

第k阶段状态的转移只依赖第k-1阶段的状态，可以用滚动数组(由于原来的空间本不大，所以代码中没有实现滚动数组)

 //#define LOCAL
 #include <iostream>
 #include <cstdio>
 #include <cstring>
 using namespace std;
 
 int dp[][][], num[][], n;
 
 bool islegal(int x, int y)
 {
     return (x>= && x<=n && y>= && y<=n);
 }
 
 int main(void)
 {
     #ifdef LOCAL
         freopen("2686in.txt", "r", stdin);
     #endif
 
     int i, j, k, d1, d2, x1, x2, y1, y2;
     while(scanf("%d", &n) == )
     {
         memset(dp, , sizeof(dp));
         for(i = ; i <= n; ++i)
             for(j = ; j <= n; ++j)
                 scanf("%d", &num[i][j]);
 
         dp[][][] = num[][];
         for(k = ; k <= *n-; ++k)
         {
             for(i = ; i <= k - ; ++i)
                 for(j = ; j <= i; ++j)
                 {//枚举两条路径在k-1步时的状态
                     for(d1 = ; d1 <= ; ++d1)
                         for(d2 = ; d2 <= ; ++d2)
                         {//共四个延伸方向
                             x1 = i + d1, y1 = k +  - x1;
                             x2 = j + d2, y2 = k +  - x2;
                             if(islegal(x1, y1) && islegal(x2, y2))
                             {
                                 if(x1 == x2)
                                     dp[k][x1][x2] = max(dp[k][x1][x2], dp[k-][i][j] + num[x1][y1]);
                                 else
                                     dp[k][x1][x2] = max(dp[k][x1][x2], dp[k-][i][j] + num[x1][y1] + num[x2][y2]);
                             }
                         }
                 }
         }
         printf("%d\n", dp[*n-][n][n]);
     }
     return ;
 }

代码君