HDU 4810 Wall Painting

Wall Painting

Time Limit: 10000/5000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 1026    Accepted Submission(s):
280

Problem Description

Ms.Fang loves painting very much. She paints GFW(Great
Funny Wall) every day. Every day before painting, she produces a wonderful color
of pigments by mixing water and some bags of pigments. On the K-th day, she will
select K specific bags of pigments and mix them to get a color of pigments which
she will use that day. When she mixes a bag of pigments with color A and a bag
of pigments with color B, she will get pigments with color A xor B.
When she
mixes two bags of pigments with the same color, she will get color zero for some
strange reasons. Now, her husband Mr.Fang has no idea about which K bags of
pigments Ms.Fang will select on the K-th day. He wonders the sum of the colors
Ms.Fang will get with 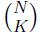different
plans.

For example, assume n = 3, K = 2 and three bags of pigments with
color 2, 1, 2. She can get color 3, 3, 0 with 3 different plans. In this
instance, the answer Mr.Fang wants to get on the second day is 3 + 3 + 0 =
6.
Mr.Fang is so busy that he doesn’t want to spend too much time on it. Can
you help him?
You should tell Mr.Fang the answer from the first day to the
n-th day.

 

Input

There are several test cases, please process till
EOF.
For each test case, the first line contains a single integer N(1 <= N
<= 10³).The second line contains N integers. The i-th integer
represents the color of the pigments in the i-th bag.

 

Output

For each test case, output N integers in a line
representing the answers(mod 10⁶ +3) from the first day to the n-th
day.

 

Sample Input

4

1 2 10 1

 

Sample Output

14 36 30 8

题意：每次从n个数字中取出i个数字，取出的这些数字亦或后得到一个值，每种情况的值求和。i 从1--n。

        其实就是cnm,的数字亦或的和。

思路：看了别人的题解才知道巧妙的地方。

如果我们把数字转换为二进制数，然后统计每位1的个数。

　　我们知道，如果我们取出的数字中，对于二进制的第i位来说，假如1的个数为偶数个，那么这一位就是为0了。

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 假如是奇数个，那么就是1。

这样我们就是知道每位的1的个数和0 的个数，cnm，凑成奇数个1.

看对于第i位来说凑成奇数个1的方案数有多少，记位num[ i ]。

那么对于第i位而已，和就是num[i] *(1<<i) ；

 

代码：

 #include<iostream>
 #include<stdio.h>
 #include<cstring>
 #include<cstdlib>
 using namespace std;
 typedef __int64 LL;

 const LL p = 1e6+;
 int a[];
 LL cnm[][];
 LL hxl[];

 void Init()
 {
     for(int i=;i<=;i++)
     {
         cnm[i][i]= ;
         cnm[i][]= i;
         cnm[i][]=;
     }
     cnm[][]=;
     for(int i=;i<=;i++)
     {
         for(int j=;j<=i;j++)
         {
             if(i==j)cnm[i][j]=;
             else if(j==) cnm[i][j]=i;
             else cnm[i][j] = (cnm[i-][j]+cnm[i-][j-])%p;
         }
     }
     hxl[]=;
     for(int i=;i<=;i++)
         hxl[i]=(hxl[i-]*)%p;
 }
 int main()
 {
     Init();
     int n;
     LL x;
     while(scanf("%d",&n)>)
     {
         if(n==)
         {
             scanf("%I64d",&x);
             printf("%I64d\n",x%p);
             continue;
         }
         memset(a,,sizeof(a));
         for(int i=;i<=n;i++)
         {
             scanf("%I64d",&x);
             int len = ;
             while(x)
             {
                 ++len;
                 a[len] = a[len]+(x&);
                 x=x>>;
             }
         }
         LL sum ;
         for(int m=;m<=n;m++)//枚举一次取几个数字
         {
             sum = ;
             for(int j=;j<=;j++)//枚举每一个位
             {
                 for(int i=;i<=a[j]&&i<=m;i=i+)//每一位上取1的个数
                 {
                     //if(cnm[n-a[j]][m-i])
                     sum = (sum+(hxl[j]*(cnm[a[j]][i]*cnm[n-a[j]][m-i])%p)%p)%p;
                 }
             }
             printf("%I64d",sum);
             if(m!=n) printf(" ");
             else printf("\n");
         }
     }
     return ;
 }