数据结构（三）串---KMP模式匹配算法

（一）定义

由于BF模式匹配算法的低效（有太多不必要的回溯和匹配），于是某三个前辈发表了一个模式匹配算法，可以大大避免重复遍历的情况，称之为克努特-莫里斯-普拉特算法，简称KMP算法

（二）KMP算法了解

问题由模式串T决定，而不是由目标串S决定

可以避免不必要的回溯和多余的匹配

1.思路启发一（避免了所有的回溯）：

前提：对于模式串和目标串的匹配，我们在前4个完全匹配，直到i5与j5才失配

上面匹配到j5与i5时失配，那么我们下一步应该如何匹配呢？是按照BF算法回溯到i=i-j+-->i2处继续与T重新匹配吗？
当然不是，我们这里讲的KMP算法就是为了避免不必要的回溯而出现的！那么我们如何避免不必要的回溯呢？什么是不必要的回溯？

什么是不必要的回溯（记住重点是模式串）：

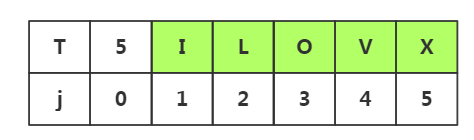
在模式串中我们已经发现了：j1≠j2≠j3≠j4≠j5

而在前提中我们已经直到了前面四个已经和目标串匹配了，也就是说i1=j1,i2=j2,i3=j3,i4=j4.

由上面两句话，那么我们就已经知道j1≠i2≠i3≠i4,所以我们没有必要回溯到i2,i3或者i4去重新匹配，我们应该直接去i5处进行下一次的重新匹配

下一次的匹配（从i5开始）：

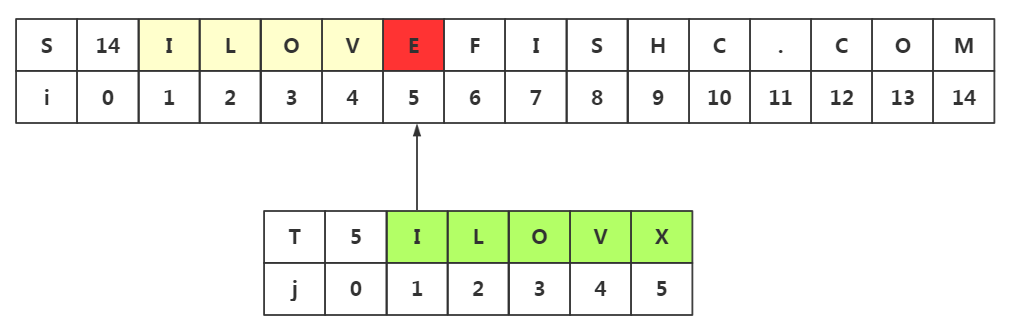
2.思路启发二（不必要的回溯不代表不会回溯，若是需要回溯，那么一定是不可避免的回溯）

前提：模式串中j1=j2≠j3,我们知道目标串S前两个和模式串前两个是匹配的。

什么是必要的回溯？为什么不可避免？
因为当模式串中出现与首字符相同的字符时，那么就会出现不可避免的回溯

因为j1=j2,j2=i2,所以我们下次匹配要从i2处与j1进行匹配，因为我们也不确定i3是不是与j2相同，所以这里的匹配是必要的。这里我们回溯到了i=i-j+--->i2处进行匹配

居然这里的回溯是不可避免的？那么KMP的优点是不是没有了？
KMP主要是避免了不必要的回溯，还可以避免不必要的匹配！
这里我们回溯是躲不了了，那么我们看看匹配呢？发现模式串中j1=j2,j2=i2,那么j1=i2是一定的，所有我们即便回溯到了i2处，我也也可以避免掉这一次的匹配，而是直接去匹配i3和j2即可

下面引出不必要的匹配

3.思路启发三（不必要的匹配）

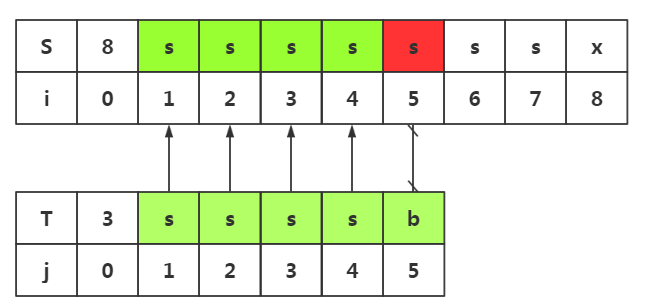
和思路二一样，我们会发现回溯是不可避免的，我们必须要回溯到i=i-j+--->i2处与T串重新匹配，那么既然不能避免不必要的回溯，我们中该有地方避免不必要的匹配吧

我们发现j1=j2=j3=j4,而前四个与目标串是匹配的，所有j1=i2,j2=i3,j3=i4这三处的匹配我们是早已经知道了，所有是没有必要的匹配

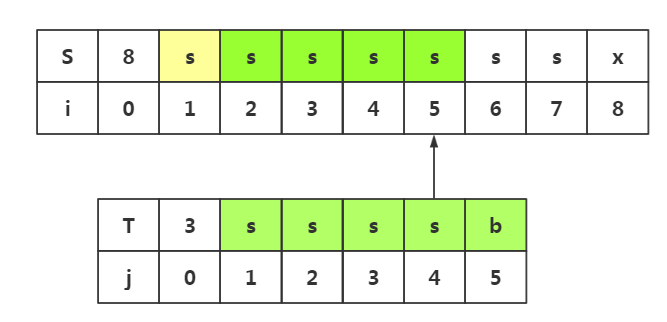
4.思路启发四（综合思路一和思路二和思路三，必要的回溯，不必要的回溯和不必要的匹配）：

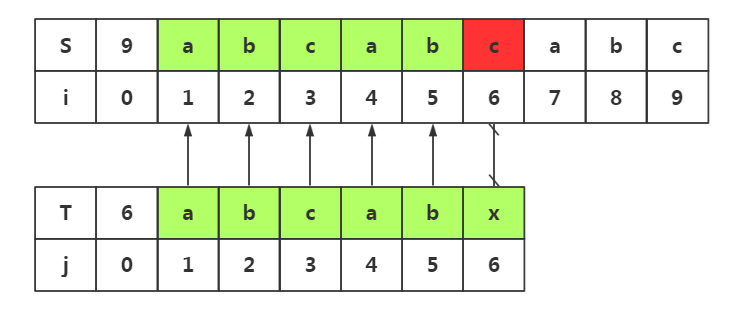
这里将会出现不必要的回溯，必要的回溯，和不必要的匹配这三种情况，是对上面两种思路的扩展

必要的回溯

由思路启发二：我们可以知道，回溯的与否取决于模式串中是否有和模式串首字符相同的位置。而这里j1=j4,j4=i4，所有我们j1与i4的匹配是必要的。

然而在直接匹配j1和i4之前，我们要确定前面的j1与i2,i3是不必要的回溯

不必要的回溯

我们发现j1≠j2≠j3,那么当我们进行回溯时就不需要考虑j1与i2,i3的情况了，这就是不必要的回溯

所以我们回溯到的位置如下

不必要的匹配

查看模式串，我们知道j1=j4=i4,j2=j5=i5,那么我们现在是回溯到了j1=j4处，我们早已经找到j1=i4,j2=i5所以这两处的匹配就是不必要的，我们需要直接去匹配j3与i6即可

思路总结：

KMP算法的优化存在两个方面
1.回溯i值
2.匹配j值

且两者必定存在一个，若是无法避免回溯，那么对于j1一定可以避免一次匹配

（三）next数组

我们可以知道回溯是与模式串T中首字符是否在T串后面的字符中存在有关，所有回溯i值与j值有关。

所以我们下面就主要考虑j值，j值与主串没有什么关系，关键就取决于T串的结构中是否有重复的问题，而j值的多少在于当前字符之前的串的前缀和后缀的相似度。

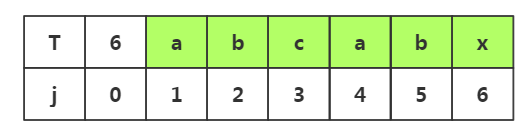
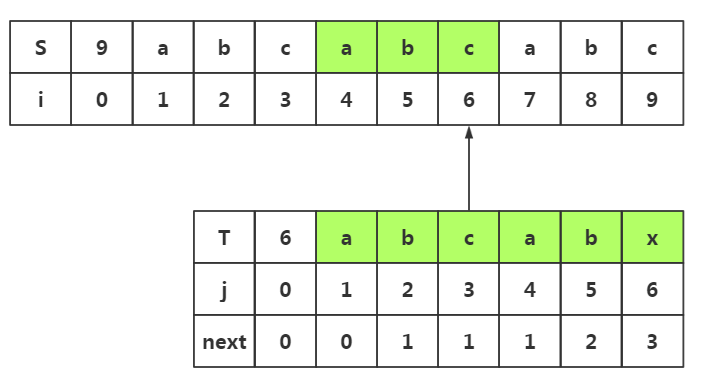
T="abcabx",我们获取x处的j值，需要取决于他前面的串abcab的前后缀的相似度，发现前缀ab与后缀ab相同，所有j值为3（相似度加一）

我们把T串的各个位置的j值变化定义为一个数组next,那么next的长度就是T串的长度，next函数定义为：

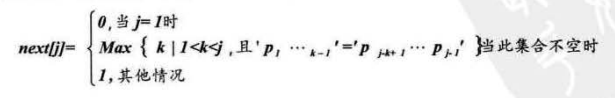
其中p1.....pk-1是前缀，pj-k+....pj-1是后缀

注意：前后缀是我们获取j值之前的子串中的子串

next数组推导

推导一：

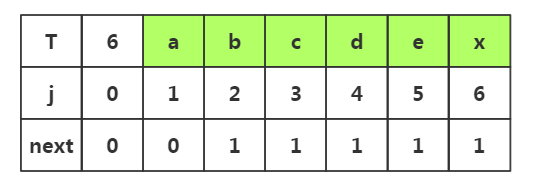
1.j=1时，next[1]=0

2.j=2时，1<k<2不存在，是其他情况，next[2]=1

3.j=3时，1<k<3,k取2，子串是p1--pj-1是'ab'串，其前缀为p1...pk-1==p1='a',后缀为pj-k+1....pj-1==p2='b'相似度为空，所有是其他情况,next[3]=1

4.j=4时，1<k<4,k可以取2,3，子串是p1-pj-1是'abc'串，当k取2时前缀为p1='a'，后缀为p2='b';当k=3时，前缀p1p2='ab',后缀p2p3='bc';集合k值为空时其他情况，所以next[4]=1。

注意：此处开始k取值情况变多，推导变多。所以我们可以在获取了子串后，直接观察子串的前后缀的相似度情况，k值就是其相似度+1后的值

5.j=5时，1<k<5,子串是p1-pj-1是串'abcd'，其子串相似度为0，所以属于其他情况，所以next[5]=1

6.j=6时，1<k<6,子串是p1-pj-1是串'abcde',其子串相似度为0，所以属于其他情况，所以next[6]=1

推导二：

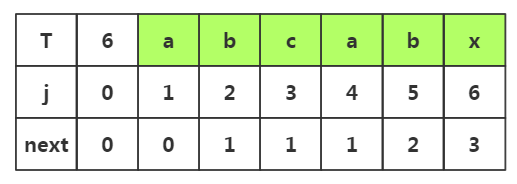
1.j=1时，next[1]=0

2.j=2时，1<k<2不存在，是其他情况，next[2]=1

注意：j=1和j=2基本是固定的了next[]=,next[]=

3.j=3时，1<k<3,子串p1-p2是串'ab',前后缀相似度为0，是其他情况，所以next[3]=1

4.j=4时，1<k<4,子串是p1-p3是'abc'串，前后缀相似度为0，是其他情况，所以next[4]=1

4.j=5时，1<k<5,子串是p1-p4是'abca'串，前后缀相似度为1，k值为1+1=2，所以next[4]=2

5.j=6时，1<k<6,子串是p1-p5是'abcab'串，前后缀相似度为2，k值为2+1=2，所以next[4]=3

推导三：

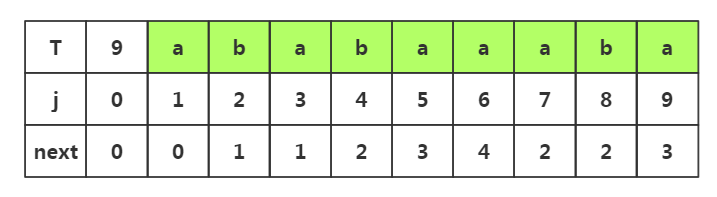
1.j=1时，next[1]=0

2.j=2时，1<k<2不存在，是其他情况，next[2]=1

3.j=3时，1<k<3,子串p1-p2是串'ab',前后缀相似度为0，是其他情况，所以next[3]=1

4.j=4时，1<k<4,子串是p1-p3是'aba'串，前后缀相似度为1，k=1+1，所以next[4]=2

5.j=5时，1<k<5,子串是p1-p4是'abab'串，前后缀相似度为2，k=2+1，所以next[5]=3

6.j=6时，1<k<6,子串是p1-p5是'ababa'串，前'aba'后'aba'缀相似度为3，k=3+1，所以next[6]=4

7.j=7时，1<k<7,子串是p1-p6是'ababaa'串，前'a'后'a'缀相似度为1，k=1+1，所以next[7]=2

8.j=8时，1<k<8,子串是p1-p7是'ababaaa'串，前'a'后'a'缀相似度为1，k=1+1，所以next[8]=2

9.j=9时，1<k<9,子串是p1-p8是'ababaaab'串，前'ab'后'ab'缀相似度为2，k=2+1，所以next[9]=3

推导四：

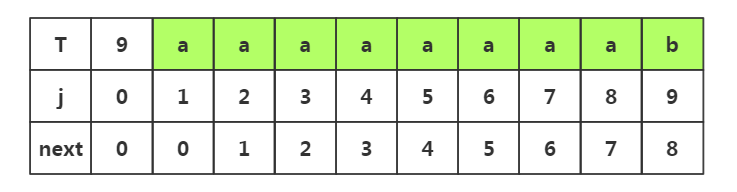
1.j=1时，next[1]=0

2.j=2时，1<k<2不存在，是其他情况，next[2]=1

3.j=3时，1<k<3,子串p1-p2是串'aa',前后缀相似度为1，k=1+1，所以next[3]=2

4.j=4时，1<k<4,子串是p1-p3是'aaa'串，前后缀相似度为2，k=2+1，所以next[4]=3

5.j=5时，1<k<5,子串是p1-p4是'aaaa'串，前后缀相似度为3，k=3+1，所以next[5]=4

6.j=6时，1<k<6,子串是p1-p5是'aaaaa'串，前后缀相似度为4，k=4+1，所以next[6]=5

7.j=7时，1<k<7,子串是p1-p6是'aaaaaa'串，前后缀相似度为5，k=5+1，所以next[7]=6

8.j=8时，1<k<8,子串是p1-p7是'aaaaaaa'串，前后缀相似度为6，k=6+1，所以next[8]=7

9.j=9时，1<k<9,子串是p1-p8是'aaaaaaaa'串，前后缀相似度为7，k=7+1，所以next[9]=8

推导五：（我们通过看图可以更加快的获取next[j]值，也方便了解）

对于j=1和j=2是不变的，值始终一样为0和1

现在我们想随机获取j=4时，next[j]的值，不经过太麻烦的方法即可得出

我们直接来看他的子串的前后缀相似度即可

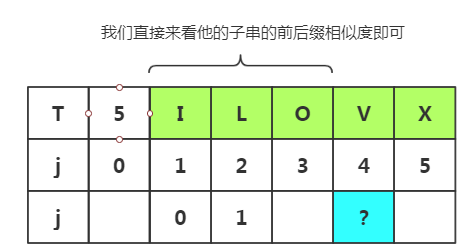
可以看出相似度为0，属于其他情况，k=

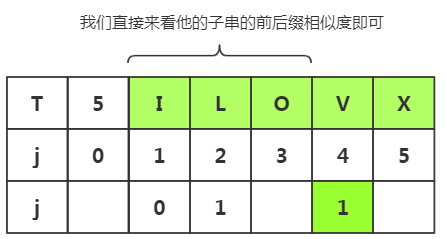
这种推导更容易我们理解程序的实现

推导总结

next[j]表示当前模式串T的j下标对目标串S的i值失配时，我们应该使用模式串的下标为next[j]接着去和目标串失配的i值进行匹配

next数组使用1：避免不必要匹配

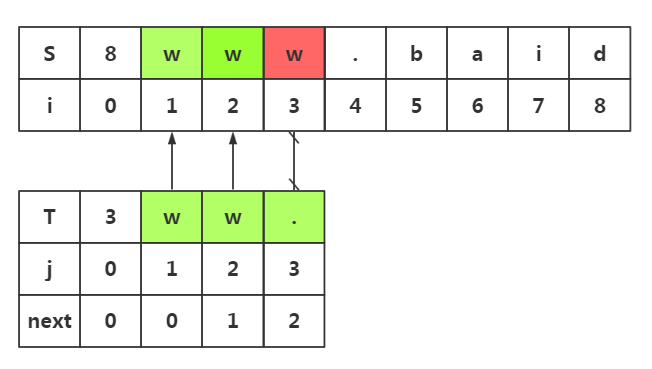
.我们在i=3与j=3处失配了
.我们在模式串中获取next[j]-->next[]=
.所以我们在目标串失配处i=3处和模式串T下标为2的数据开始匹配即可

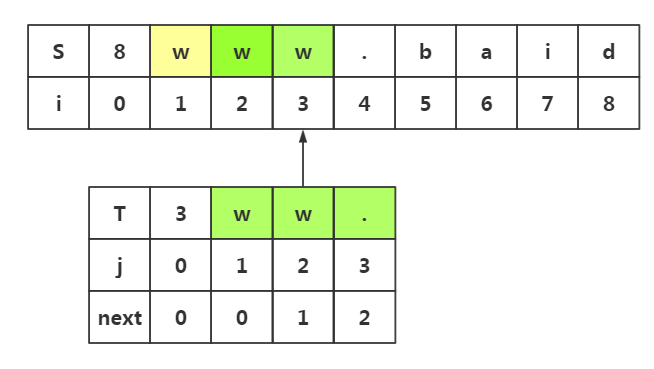
这样就避免了不必要的匹配，当然我们使用上面的其他思路，也会发现可以避免不必要的回溯

next数组使用1：避免不必要回溯

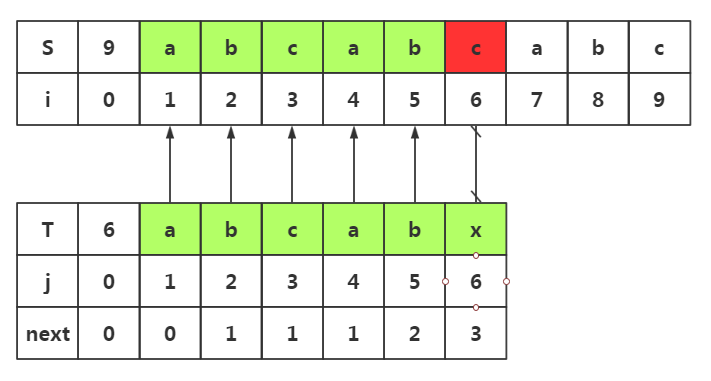
.我们在i=6与j=6处失配了
.我们在模式串中获取next[j]-->next[]=
.所以我们在目标串失配处i=6处和模式串T下标为3的数据开始匹配即可