HDU 4453 Looploop （伸展树splay tree）

Looploop

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 781    Accepted Submission(s): 220

Problem Description

XXX gets a new toy named Looploop. The toy has N elements arranged in a loop, an arrow pointing to one of the elements, and two preset parameters k1 and k2. Every element has a number on it.

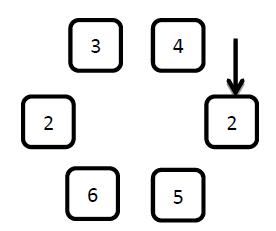
The figure above shows a Looploop of 6 elments. Let's assuming the preset parameter k1 is 3, and k2 is 4.
XXX can do six operations with the toy.

1: add x 
Starting from the arrow pointed element, add x to the number on the clockwise first k2 elements.

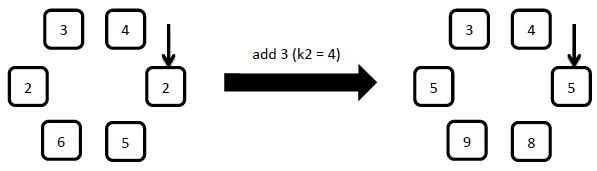
2: reverse
Starting from the arrow pointed element, reverse the first k1 clockwise elements.

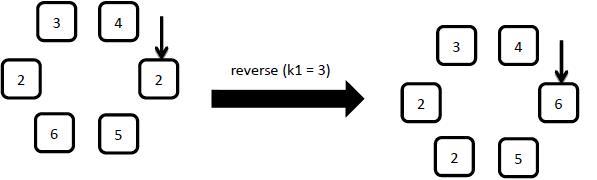
3: insert x 
Insert a new element with number x to the right (along clockwise) of the arrow pointed element.

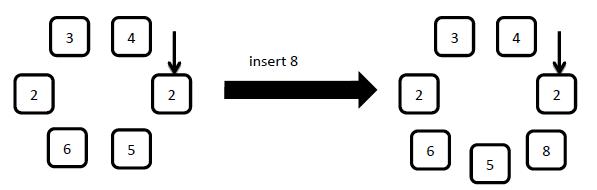
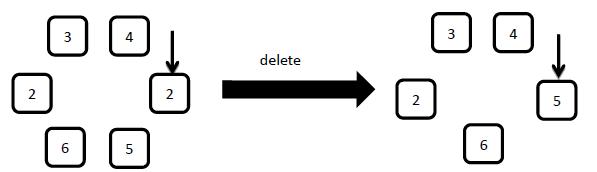
4: delete 
Delete the element the arrow pointed and then move the arrow to the right element.

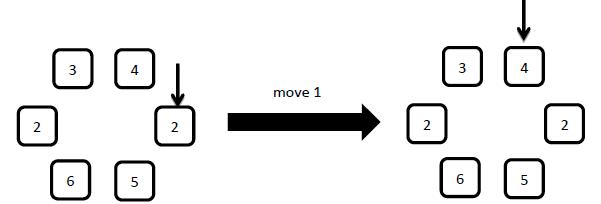
5: move x 
x can only be 1 or 2. If x = 1 , move the arrow to the left(along the counterclockwise) element, if x = 2 move the arrow to the right element.

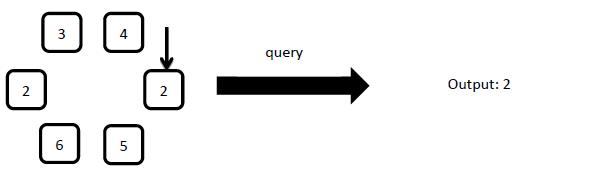
6: query
Output the number on the arrow pointed element in one line.

XXX wants to give answers to every query in a serial of operations.

 

Input

There are multiple test cases.
For each test case the first line contains N,M,k1,k2(2≤k1<k2≤N≤10⁵, M≤10⁵) indicating the initial number of elements, the total number of operations XXX will do and the two preset parameters of the toy. 
Second line contains N integers ai(-10⁴≤ai≤10⁴) representing the N numbers on the elements in Looploop along clockwise direction. The arrow points to first element in input at the beginning. 
Then m lines follow, each line contains one of the six operations described above.
It is guaranteed that the "x" in the "add","insert" and "move" operations is always integer and its absolute value ≤104. The number of elements will never be less than N during the operations. 
The input ends with a line of 0 0 0 0.

 

Output

For each test case, output case number in the first line(formatted as the sample output). Then for each query in the case, output the number on the arrow pointed element in a single line.

 

Sample Input

5 1 2 4
3 4 5 6 7
query
5 13 2 4
1 2 3 4 5
move 2
query
insert 8
reverse
query
add 2
query
move 1
query
move 1
query
delete
query
0 0 0 0

 

Sample Output

Case #1:
3
Case #2:
2
8
10
1
5
1

 

Source

2012 Asia Hangzhou Regional Contest

 

用splay tree解决很容易实现。

 /* ***********************************************
 Author        :kuangbin
 Created Time  :2013-10-22 16:10:40
 ************************************************ */
 
 #include <stdio.h>
 #include <string.h>
 #include <iostream>
 #include <algorithm>
 #include <vector>
 #include <queue>
 #include <set>
 #include <map>
 #include <string>
 #include <math.h>
 #include <stdlib.h>
 #include <time.h>
 using namespace std;
 
 #define Key_value ch[ch[root][1]][0]
 const int MAXN = ;
 
 int pre[MAXN],ch[MAXN][],key[MAXN],size[MAXN];
 int root,tot1;
 int s[MAXN],tot2;
 int rev[MAXN],add[MAXN];
 int n,q,k1,k2;
 int a[MAXN];
 int tp;//指针
 void NewNode(int &r,int father,int k)
 {
     if(tot2)r = s[tot2--];
     else r = ++tot1;
     pre[r] = father;
     ch[r][] = ch[r][] = ;
     key[r] = k;
     add[r] = ;
     rev[r] = ;
     size[r] = ;
 }
 void Update_Rev(int r)
 {
     if(!r)return;
     swap(ch[r][],ch[r][]);
     rev[r] ^= ;
 }
 void Update_ADD(int r,int ADD)
 {
     if(!r)return;
     key[r] += ADD;
     add[r] += ADD;
 }
 
 void push_up(int r)
 {
     size[r] = size[ch[r][]] + size[ch[r][]] + ;
 }
 void push_down(int r)
 {
     if(add[r])
     {
         Update_ADD(ch[r][],add[r]);
         Update_ADD(ch[r][],add[r]);
         add[r] = ;
     }
     if(rev[r])
     {
         Update_Rev(ch[r][]);
         Update_Rev(ch[r][]);
         rev[r] = ;
     }
 }
 void Build(int &x,int l,int r,int father)
 {
     if(l > r)return;
     int mid = (l+r)/;
     NewNode(x,father,a[mid]);
     Build(ch[x][],l,mid-,x);
     Build(ch[x][],mid+,r,x);
     push_up(x);
 }
 void Init()
 {
     root = tot1 = tot2 = ;
     ch[root][] = ch[root][] = size[root] = pre[root] = ;
     rev[root] = ;
     add[root] = ;
     NewNode(root,,-);
     NewNode(ch[root][],root,-);
     for(int i = ;i < n;i++)
         scanf("%d",&a[i]);
     Build(Key_value,,n-,ch[root][]);
     push_up(ch[root][]);
     push_up(root);
 }
 //旋转，0为左旋，1为右旋
 void Rotate(int x,int kind)
 {
     int y = pre[x];
     push_down(y);
     push_down(x);
     ch[y][!kind] = ch[x][kind];
     pre[ch[x][kind]] = y;
     if(pre[y])
         ch[pre[y]][ch[pre[y]][]==y] = x;
     pre[x] = pre[y];
     ch[x][kind] = y;
     pre[y] = x;
     push_up(y);
 }
 void Splay(int r,int goal)
 {
     push_down(r);
     while(pre[r] != goal)
     {
         if(pre[pre[r]] == goal)
         {
             push_down(pre[r]);
             push_down(r);
             Rotate(r,ch[pre[r]][] == r);
         }
         else
         {
             push_down(pre[pre[r]]);
             push_down(pre[r]);
             push_down(r);
             int y = pre[r];
             int kind = ch[pre[y]][]==y;
             if(ch[y][kind] == r)
             {
                 Rotate(r,!kind);
                 Rotate(r,kind);
             }
             else
             {
                 Rotate(y,kind);
                 Rotate(r,kind);
             }
         }
     }
     push_up(r);
     if(goal == ) root = r;
 }
 int Get_kth(int r,int k)
 {
     push_down(r);
     int t = size[ch[r][]] + ;
     if(t == k)return r;
     if(t > k)return Get_kth(ch[r][],k);
     else return Get_kth(ch[r][],k-t);
 }
 void ADD(int x)
 {
     //先搬移动
     Splay(tp,);
     int tmp = size[ch[root][]] + ;
     Splay(Get_kth(root,),);
     Splay(Get_kth(root,tmp),root);
     tmp = Key_value;
     Key_value = ;
     push_up(ch[root][]);
     push_up(root);
     Splay(Get_kth(root,size[root] - ),);
     Key_value = tmp;
     pre[Key_value] = ch[root][];
     push_up(ch[root][]);
     push_up(root);
     Splay(Get_kth(root,),);
     Splay(Get_kth(root,k2+),root);
     Update_ADD(Key_value,x);
     push_up(ch[root][]);
     push_up(root);
     tp = Get_kth(root,);
 }
 void REVERSE()
 {
     Splay(tp,);
     int tmp = size[ch[root][]] + ;
     Splay(Get_kth(root,),);
     Splay(Get_kth(root,tmp),root);
     tmp = Key_value;
     Key_value = ;
     push_up(ch[root][]);
     push_up(root);
     Splay(Get_kth(root,size[root] - ),);
     Key_value = tmp;
     pre[Key_value] = ch[root][];
     push_up(ch[root][]);
     push_up(root);
     Splay(Get_kth(root,),);
     Splay(Get_kth(root,k1+),root);
     Update_Rev(Key_value);
     push_up(ch[root][]);
     push_up(root);
     tp = Get_kth(root,);
 }
 void INSERT(int x)
 {
     Splay(tp,);
     //printf("%d %d\n",tp,size[ch[root][0]]+2);
     int tt = Get_kth(root,size[ch[root][]]+);
     //printf("%d %d %d\n",Get_kth(root,size[ch[root][0]]+2),tt,key[tt]);
     Splay(Get_kth(root,size[ch[root][]]+),root);
     NewNode(Key_value,ch[root][],x);
     push_up(ch[root][]);
     push_up(root);
 }
 void DELETE()
 {
     Splay(tp,);
     int tmp = size[ch[root][]] + ;
     Splay(Get_kth(root,tmp-),);
     Splay(Get_kth(root,tmp+),root);
     s[++tot2] = Key_value;
     Key_value = ;
     push_up(ch[root][]);
     push_up(root);
     if(tmp == size[root])tp = Get_kth(root,);
     else tp = Get_kth(root,tmp);
 }
 int MOVE(int x)
 {
     if(x == )
     {
         Splay(tp,);
         int tmp = size[ch[root][]] + ;
         tmp--;
         if(tmp == )tmp = size[root] - ;
         tp = Get_kth(root,tmp);
     }
     else
     {
         Splay(tp,);
         int tmp = size[ch[root][]] + ;
         tmp++;
         if(tmp == size[root])tmp = ;
         tp = Get_kth(root,tmp);
         //cout<<tp<<endl;
     }
 }
 int query()
 {
     Splay(tp,);
     return key[root];
 }
 char op[];
 int x;
 int main()
 {
     //freopen("in.txt","r",stdin);
     //freopen("out.txt","w",stdout);
     int iCase = ;
     while(scanf("%d%d%d%d",&n,&q,&k1,&k2) == )
     {
         if(n ==  && q ==  && k1 ==  && k2 == )break;
         iCase ++;
         printf("Case #%d:\n",iCase);
         Init();
         tp = Get_kth(root,);
         while(q--)
         {
             scanf("%s",op);
             if(op[] == 'a')
             {
                 scanf("%d",&x);
                 ADD(x);
             }
             else if(op[] == 'r')
                 REVERSE();
             else if(op[] == 'i')
             {
                 scanf("%d",&x);
                 INSERT(x);
             }
             else if(op[] == 'd')
                 DELETE();
             else if(op[] == 'm')
             {
                 scanf("%d",&x);
                 MOVE(x);
             }
             else printf("%d\n",query());
         }
 
     }
     return ;
 }