LOJ2542 PKUWC2018随机游走（概率期望+容斥原理）

　　如果直接dp，状态里肯定要带上已走过的点的集合，感觉上不太好做。

　　考虑一种对期望的minmax容斥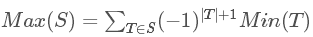：其中Max(S)为遍历完S集合的期望步数，Min(S)为遍历到S集合中一个点的期望步数。当然才不管怎么证，反正看上去非常优美。

　　设f[i][S]为由i节点出发的Min(S)，显然有f[i][S]=Σf[j][S]/d_i+1。暴力高斯消元复杂度就炸掉了。

　　注意到给出的是一棵树，现在连这个性质都没用到当然没法做。根据一个我没见过的套路，可以考虑把f[i]表示成a·f[fa]+b的形式，大力推一波式子就可以了。

　　求出f后，暴力枚举子集容斥进行预处理是O(3ⁿ)的，类似高维前缀和直接递推就是O(2ⁿn)。然后就可以O(1)回答每个询问了。

#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstdlib>
#include<cstring>
#include<algorithm>
using namespace std;
#define ll long long
#define N 18
#define P 998244353
char getc(){char c=getchar();while ((c<'A'||c>'Z')&&(c<'a'||c>'z')&&(c<''||c>'')) c=getchar();return c;}
int gcd(int n,int m){return m==?n:gcd(m,n%m);}
int read()
{
    int x=,f=;char c=getchar();
    while (c<''||c>'') {if (c=='-') f=-;c=getchar();}
    while (c>=''&&c<='') x=(x<<)+(x<<)+(c^),c=getchar();
    return x*f;
}
int n,m,S,p[N],f[N][<<N],size[<<N],d[N],a[N],b[N],t;
struct data{int to,nxt;
}edge[N<<];
void addedge(int x,int y){t++;edge[t].to=y,edge[t].nxt=p[x],p[x]=t;}
int ksm(int a,int k)
{
    int s=;
    for (;k;k>>=,a=1ll*a*a%P) if (k&) s=1ll*s*a%P;
    return s;
}
int inv(int a){return ksm(a,P-);}
void dfs(int k,int from,int S)
{
    for (int i=p[k];i;i=edge[i].nxt)
    if (edge[i].to!=from) dfs(edge[i].to,k,S);
    if (S&(<<k)) a[k]=b[k]=;
    else
    {
        int A=,B=;
        for (int i=p[k];i;i=edge[i].nxt)
        if (edge[i].to!=from) A=(A+a[edge[i].to])%P,B=(B+b[edge[i].to])%P;
        a[k]=inv((d[k]-A+P)%P),b[k]=1ll*(B+d[k])*a[k]%P;
    }
}
void dfs2(int k,int from,int S)
{
    for (int i=p[k];i;i=edge[i].nxt)
    if (edge[i].to!=from)
    {
        f[edge[i].to][S]=(1ll*a[edge[i].to]*f[k][S]+b[edge[i].to])%P;
        dfs2(edge[i].to,k,S);
    }
}
int main()
{
#ifndef ONLINE_JUDGE
    freopen("loj2542.in","r",stdin);
    freopen("loj2542.out","w",stdout);
    const char LL[]="%I64d\n";
#else
    const char LL[]="%lld\n";
#endif
    n=read(),m=read(),S=read()-;
    for (int i=;i<n;i++)
    {
        int x=read()-,y=read()-;
        addedge(x,y),addedge(y,x);
        d[x]++,d[y]++;
    }
    for (int i=;i<(<<n);i++)
        for (int j=;j<n;j++)
        if (i&(<<j)) {dfs(j,j,i);dfs2(j,j,i);break;}
    for (int i=;i<(<<n);i++)
    {
        size[i]=size[i^(i&-i)]+;
        if (!(size[i]&)) f[S][i]=(P-f[S][i])%P;
    }
    for (int i=;i<n;i++)
        for (int j=;j<(<<n);j++)
        if (j&(<<i)) f[S][j]=(f[S][j]+f[S][j^(<<i)])%P;
    /*for (int i=(1<<n)-1;i;i--)
        for (int j=i^(i&-i);j;j=j-1&i)
        f[S][i]=(f[S][i]+f[S][j])%P;*/
    while (m--)
    {
        int k=read(),x=;
        for (int i=;i<=k;i++) x|=<<read()-;
        printf("%d\n",f[S][x]);
    }
    return ;
}