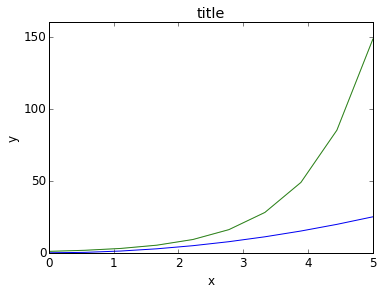
python数据分析之matplotlib学习
本文作为学习过程中对matplotlib一些常用知识点的整理,方便查找。
类MATLAB API
最简单的入门是从类 MATLAB API 开始,它被设计成兼容 MATLAB 绘图函数。
from pylab import *
from numpy import *
x = linspace(0, 5, 10)
y = x ** 2
figure()
plot(x, y, 'r')
xlabel('x')
ylabel('y')
title('title')
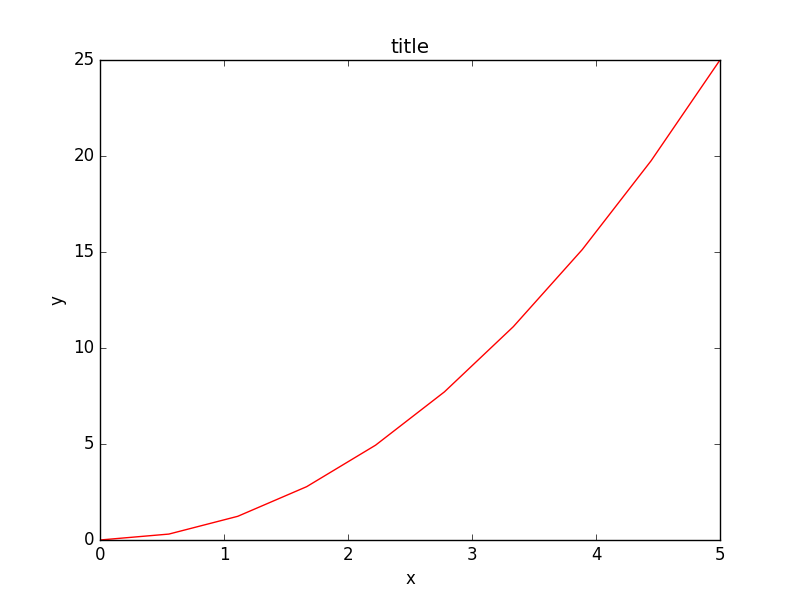
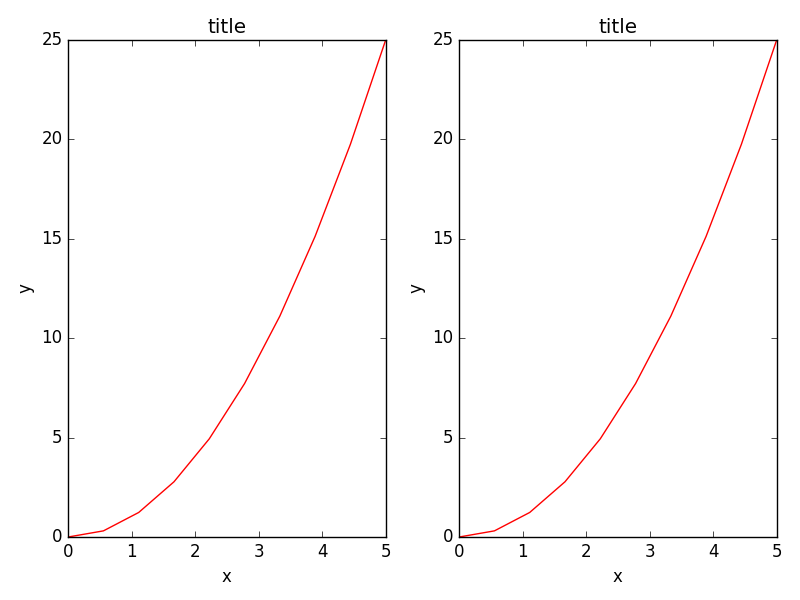
创建子图,选择绘图用的颜色与描点符号:
subplot(1,2,1)
plot(x, y, 'r--')
subplot(1,2,2)
plot(y, x, 'g*-');
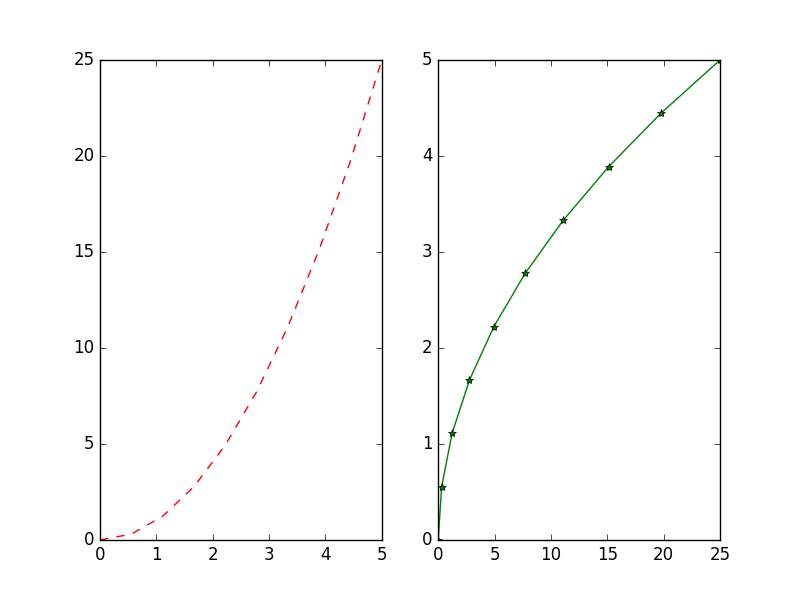
linspace表示在0到5之间用10个点表示,plot的第三个参数表示画线的颜色与样式
此类 API 的好处是可以节省你的代码量,但是我们并不鼓励使用它处理复杂的图表。处理复杂图表时, matplotlib 面向对象 API 是一个更好的选择。
matplotlib 面向对象 API
使用面向对象API的方法和之前例子里的看起来很类似,不同的是,我们并不创建一个全局实例,而是将新建实例的引用保存在 fig 变量中,如果我们想在图中新建一个坐标轴实例,只需要 调用 fig 实例的 add_axes 方法:
import matplotlib.pyplot as plt
from pylab import *
x = linspace(0, 5, 10)
y = x ** 2
fig = plt.figure()
axes = fig.add_axes([0.1, 0.1, 0.8, 0.8]) # left, bottom, width, height (range 0 to 1)
axes.plot(x, y, 'r')
axes.set_xlabel('x')
axes.set_ylabel('y')
axes.set_title('title')
plt.show()
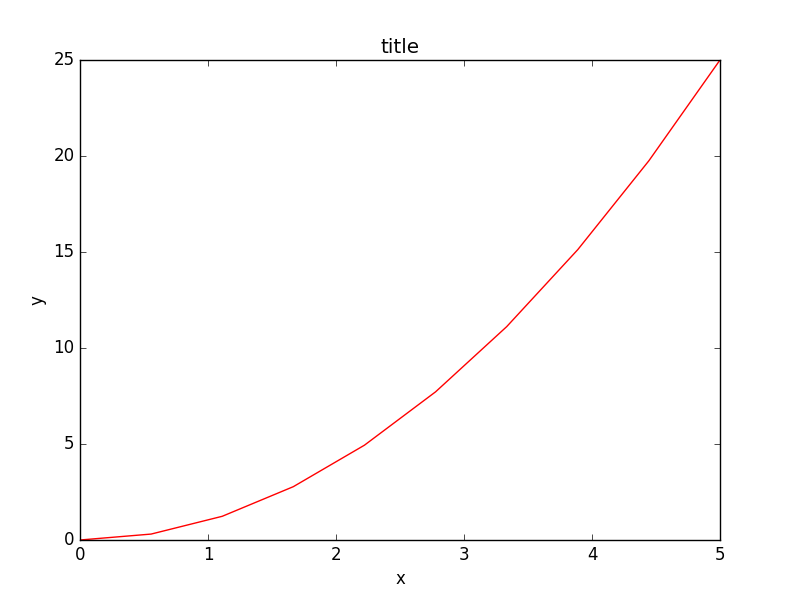
尽管会写更多的代码,好处在于我们对于图表的绘制有了完全的控制权,可以很容易地多加一个坐标轴到图中:
import matplotlib.pyplot as plt
from pylab import *
x = linspace(0, 5, 10)
y = x ** 2
fig = plt.figure()
axes = fig.add_axes([0.1, 0.1, 0.8, 0.8]) # left, bottom, width, height (range 0 to 1)
axes2 = fig.add_axes([0.2, 0.5, 0.4, 0.3]) # inset axes
axes.plot(x, y, 'r')
axes.set_xlabel('x')
axes.set_ylabel('y')
axes.set_title('title')
# insert
axes2.plot(y, x, 'g')
axes2.set_xlabel('y')
axes2.set_ylabel('x')
axes2.set_title('insert title');
plt.show()
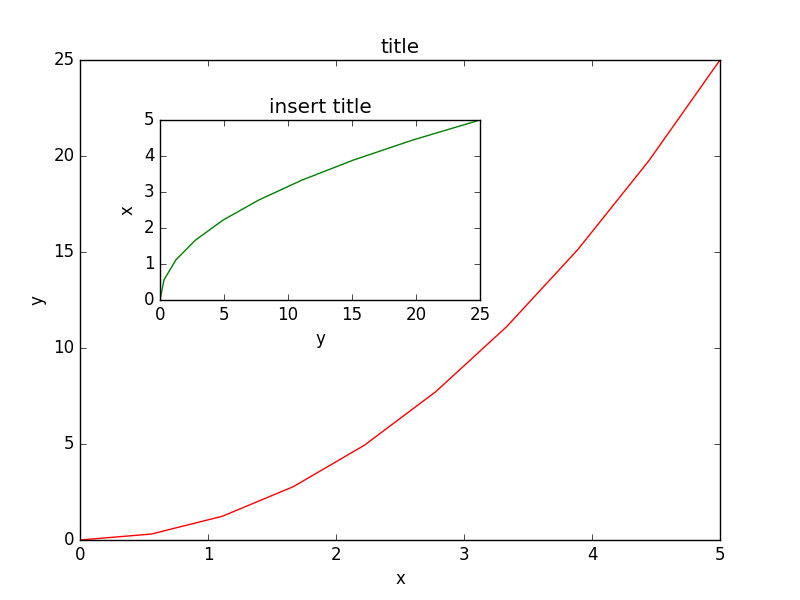
如果我们不在意坐标轴在图中的排放位置️,那么就可以使用matplotlib的布局管理器了,我最喜欢的是subplots,使用方式如下:
import matplotlib.pyplot as plt
from pylab import *
x = linspace(0, 5, 10)
y = x ** 2
fig, axes = plt.subplots(nrows=1, ncols=2)
for ax in axes:
ax.plot(x, y, 'r')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_title('title')
fig.tight_layout()
plt.show()
图表尺寸,长宽比 与 DPI
在创建 Figure 对象的时候,使用figsize 与 dpi 参数能够设置图表尺寸与DPI, 创建一个800*400像素,每英寸100像素的图就可以这么做:
fig = plt.figure(figsize=(8,4), dpi=100)
<matplotlib.figure.Figure at 0x4cbd390>
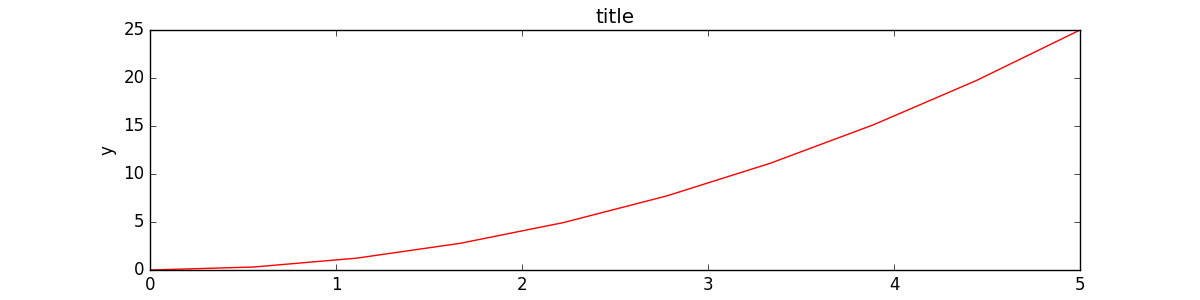
同样的参数也可以用在布局管理器上:
fig, axes = plt.subplots(figsize=(12,3))
axes.plot(x, y, 'r')
axes.set_xlabel('x')
axes.set_ylabel('y')
axes.set_title('title');
保存图表
可以使用 savefig 保存图表
fig.savefig("filename.png")
这里我们也可以有选择地指定DPI,并且选择不同的输出格式:
fig.savefig("filename.png", dpi=200)
有哪些格式?哪种格式能获得最佳质量?
Matplotlib 可以生成多种格式的高质量图像,包括PNG,JPG,EPS,SVG,PGF 和 PDF。如果是科学论文的话,我建议尽量使用pdf格式。 (pdflatex 编译的 LaTeX 文档使用 includegraphics 命令就能包含 PDF 文件)。 一些情况下,PGF也是一个很好的选择。
图例,轴标 与 标题
现在我们已经介绍了如何创建图表画布以及如何添加新的坐标轴实例,让我们看一看如何加上标题,轴标和图例
标题
每一个坐标轴实例都可以加上一个标题,只需调用坐标轴实例的 set_title 方法:
ax.set_title("title");
轴标
类似的, set_xlabel 与 set_ylabel 可以设置坐标轴的x轴与y轴的标签。
ax.set_xlabel("x")
ax.set_ylabel("y");
图例
有两种方法在图中加入图例。一种是调用坐标轴对象的 legend 方法,传入与之前定义的几条曲线相对应地图例文字的 列表/元组:
ax.legend([“curve1”, “curve2”, “curve3”]);
不过这种方式容易出错,比如增加了新的曲线或者移除了某条曲线。更好的方式是在调用 plot方法时使用 label=”label text” 参数,再调用 legend 方法加入图例:
ax.plot(x, x**2, label="curve1")
ax.plot(x, x**3, label="curve2")
ax.legend();
legend 还有一个可选参数 loc 决定画出图例的位置,详情见:http://matplotlib.org/users/legend_guide.html#legend-location
最常用的值如下:
ax.legend(loc=0) # let matplotlib decide the optimal location
ax.legend(loc=1) # upper right corner
ax.legend(loc=2) # upper left corner
ax.legend(loc=3) # lower left corner
ax.legend(loc=4) # lower right corner
# .. many more options are available
=> <matplotlib.legend.Legend at 0x4c863d0>
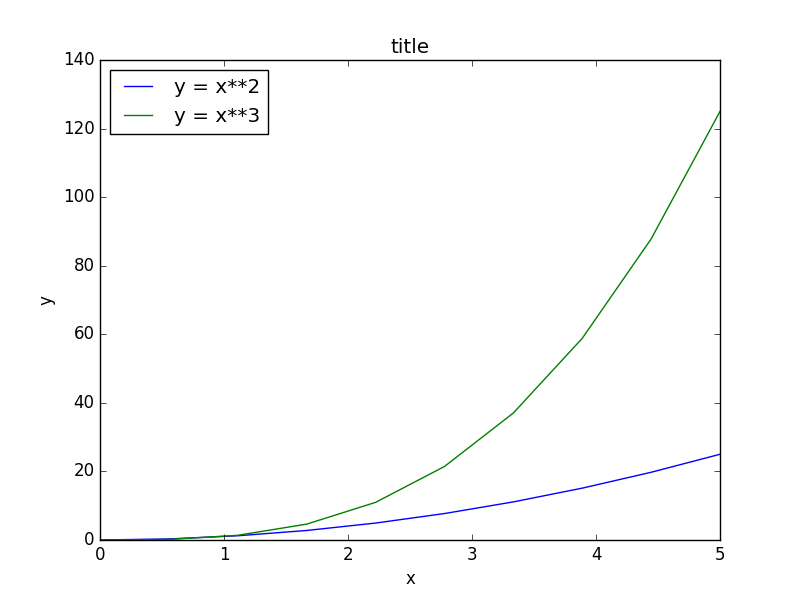
下面这个例子同时包含了标题,轴标,与图例的用法:
import matplotlib.pyplot as plt
from pylab import *
x = linspace(0, 5, 10)
y = x ** 2
fig, ax = plt.subplots()
ax.plot(x, x**2, label="y = x**2")
ax.plot(x, x**3, label="y = x**3")
ax.legend(loc=2); # upper left corner
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_title('title');
plt.show()
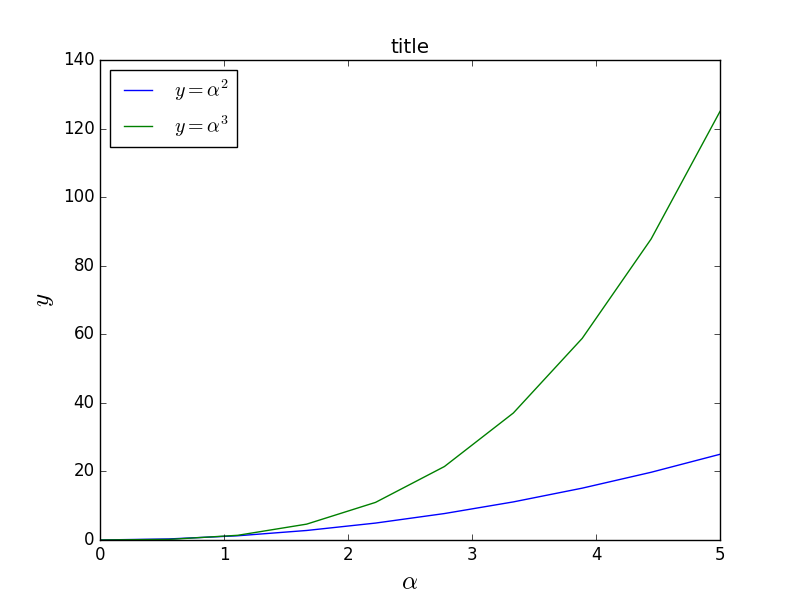
格式化文本,LaTeX,字体大小,字体类型
Matplotlib 对 LaTeX 提供了很好的支持。我们只需要将 LaTeX 表达式封装在 符号内,就可以在图的任何文本中显示了,比如“符号内,就可以在图的任何文本中显示了,比如“
不过这里我们会遇到一些小问题,在 LaTeX 中我们常常会用到反斜杠,比如 \alpha 来产生符号 αα
import matplotlib.pyplot as plt
from pylab import *
x = linspace(0, 5, 10)
y = x ** 2
fig, ax = plt.subplots()
ax.plot(x, x**2, label=r"$y = \alpha^2$")
ax.plot(x, x**3, label=r"$y = \alpha^3$")
ax.legend(loc=2) # upper left corner
ax.set_xlabel(r'$\alpha$', fontsize=18)
ax.set_ylabel(r'$y$', fontsize=18)
ax.set_title('title');
plt.show()
我们可以更改全局字体大小或者类型:
from matplotlib import rcParams
rcParams.update({'font.size': 18, 'font.family': 'serif'})
STIX 字体是一种好选择:
matplotlib.rcParams.update({'font.size': 18, 'font.family': 'STIXGeneral', 'mathtext.fontset': 'stix'})
我们也可以将图中的文本全用 Latex 渲染:
matplotlib.rcParams.update({'font.size': 18, 'text.usetex': True})
设置颜色,线宽 与 线型
颜色
有了matplotlib,我们就有很多方法能够定义线的颜色和很多其他图形元素。首先,我们可以使用类MATLAB语法,’b’ 代表蓝色,’g’ 代表绿色,依此类推。matplotlib同时也支持 MATLAB API 选择线型所使用的方式:比如 ‘b.-‘ 意味着蓝线标着点:
# MATLAB style line color and style
ax.plot(x, x**2, 'b.-') # blue line with dots
ax.plot(x, x**3, 'g--') # green dashed line
fig
=> [<matplotlib.lines.Line2D at 0x4985810>]
我们也可以以颜色的名字或者RGB值选择颜色,alpha参数决定了颜色的透明度:
fig, ax = plt.subplots()
ax.plot(x, x+1, color="red", alpha=0.5) # half-transparant red
ax.plot(x, x+2, color="#1155dd") # RGB hex code for a bluish color
ax.plot(x, x+3, color="#15cc55") # RGB hex code for a greenish color
fig
=> [<matplotlib.lines.Line2D at 0x4edbd10>]
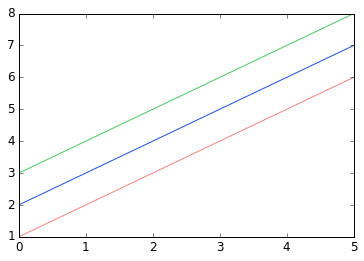
线与描点风格
linewidth 或是 lw 参数改变线宽。 linestyle 或是 ls 参数改变线的风格。
fig, ax = plt.subplots(figsize=(12,6))
ax.plot(x, x+1, color="blue", linewidth=0.25)
ax.plot(x, x+2, color="blue", linewidth=0.50)
ax.plot(x, x+3, color="blue", linewidth=1.00)
ax.plot(x, x+4, color="blue", linewidth=2.00)
# possible linestype options ‘-‘, ‘–’, ‘-.’, ‘:’, ‘steps’
ax.plot(x, x+5, color="red", lw=2, linestyle='-')
ax.plot(x, x+6, color="red", lw=2, ls='-.')
ax.plot(x, x+7, color="red", lw=2, ls=':')
# custom dash
line, = ax.plot(x, x+8, color="black", lw=1.50)
line.set_dashes([5, 10, 15, 10]) # format: line length, space length, ...
# possible marker symbols: marker = '+', 'o', '*', 's', ',', '.', '1', '2', '3', '4', ...
ax.plot(x, x+ 9, color="green", lw=2, ls='*', marker='+')
ax.plot(x, x+10, color="green", lw=2, ls='*', marker='o')
ax.plot(x, x+11, color="green", lw=2, ls='*', marker='s')
ax.plot(x, x+12, color="green", lw=2, ls='*', marker='1')
# marker size and color
ax.plot(x, x+13, color="purple", lw=1, ls='-', marker='o', markersize=2)
ax.plot(x, x+14, color="purple", lw=1, ls='-', marker='o', markersize=4)
ax.plot(x, x+15, color="purple", lw=1, ls='-', marker='o', markersize=8, markerfacecolor="red")
ax.plot(x, x+16, color="purple", lw=1, ls='-', marker='s', markersize=8,
markerfacecolor="yellow", markeredgewidth=2, markeredgecolor="blue")
fig
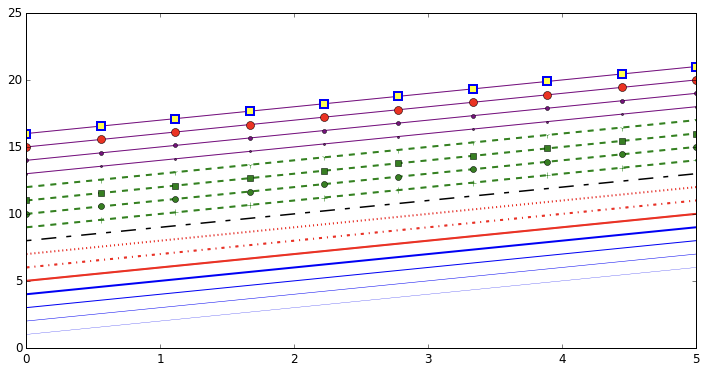
控制坐标轴的样式
坐标轴样式也是通常需要自定义的地方,像是标号或是标签的位置或是字体的大小等。
图的范围
我们想做的第一件事也许是设置坐标轴的范围,可以使用 set_ylim 或是 set_xlim 方法或者 axis(‘tight’) 自动将坐标轴调整的紧凑 The first thing we might want to configure is the ranges of the axes. We can do this using the set_ylim and set_xlim methods in the axis object, or axis(‘tight’) for automatrically getting “tightly fitted” axes ranges:
fig, axes = plt.subplots(1, 3, figsize=(12, 4))
axes[0].plot(x, x**2, x, x**3)
axes[0].set_title("default axes ranges")
axes[1].plot(x, x**2, x, x**3)
axes[1].axis('tight')
axes[1].set_title("tight axes")
axes[2].plot(x, x**2, x, x**3)
axes[2].set_ylim([0, 60])
axes[2].set_xlim([2, 5])
axes[2].set_title("custom axes range");
fig
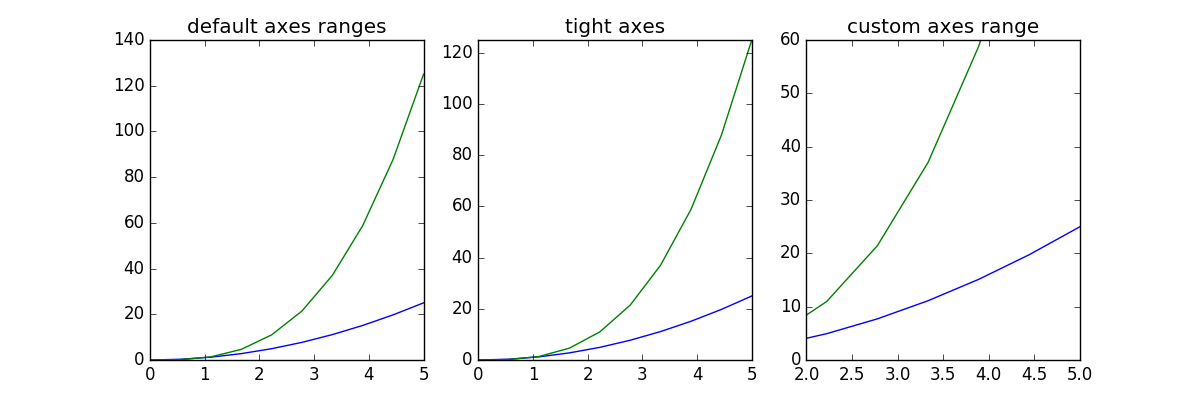
对数刻度
也可以将轴的刻度设置成对数刻度,调用 set_xscale 与 set_yscale 设置刻度,参数选择 “log” :
fig, axes = plt.subplots(1, 2, figsize=(10,4))
axes[0].plot(x, x**2, x, exp(x))
axes[0].set_title("Normal scale")
axes[1].plot(x, x**2, x, exp(x))
axes[1].set_yscale("log")
axes[1].set_title("Logarithmic scale (y)");
fig
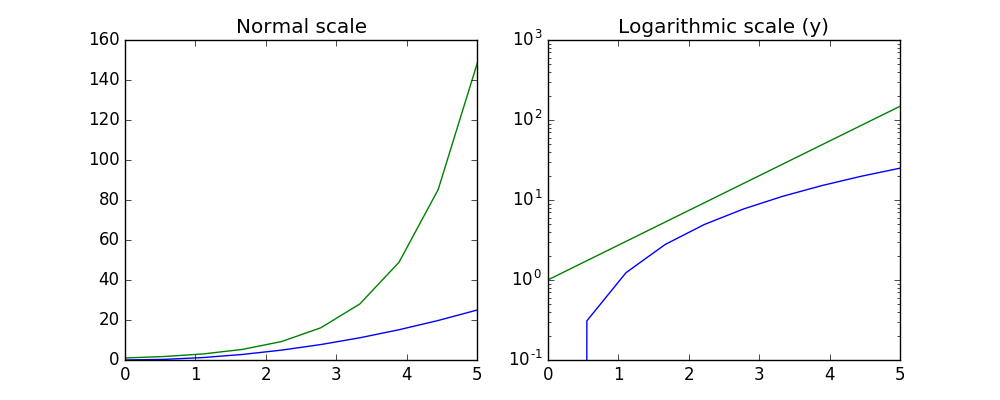
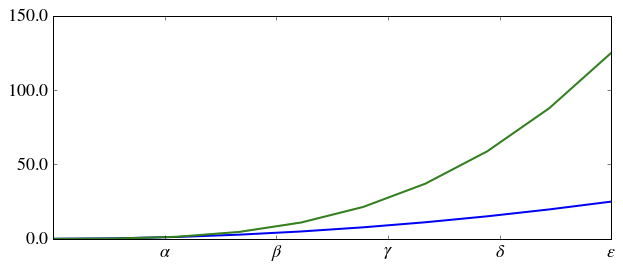
自定义标号位置与符号
set_xticks 与 set_yticks 方法可以显示地设置标号的位置, set_xticklabels 与 set_yticklabels 为每一个标号设置符号:
fig, ax = plt.subplots(figsize=(10, 4))
ax.plot(x, x**2, x, x**3, lw=2)
ax.set_xticks([1, 2, 3, 4, 5])
ax.set_xticklabels([r'$\alpha$', r'$\beta$', r'$\gamma$', r'$\delta$', r'$\epsilon$'], fontsize=18)
yticks = [0, 50, 100, 150]
ax.set_yticks(yticks)
ax.set_yticklabels(["$%.1f$" % y for y in yticks], fontsize=18); # use LaTeX formatted labels
fig
=> [<matplotlib.text.Text at 0x5d75c90>,
<matplotlib.text.Text at 0x585fe50>,
<matplotlib.text.Text at 0x575c090>,
<matplotlib.text.Text at 0x599e610>]
科学计数法
如果轴上涉及非常大的数,最好使用科学计数法:
fig, ax = plt.subplots(1, 1)
ax.plot(x, x**2, x, exp(x))
ax.set_title("scientific notation")
ax.set_yticks([0, 50, 100, 150])
from matplotlib import ticker
formatter = ticker.ScalarFormatter(useMathText=True)
formatter.set_scientific(True)
formatter.set_powerlimits((-1,1))
ax.yaxis.set_major_formatter(formatter)
fig

轴上数与标签的间距
# distance between x and y axis and the numbers on the axes
rcParams['xtick.major.pad'] = 5
rcParams['ytick.major.pad'] = 5
fig, ax = plt.subplots(1, 1)
ax.plot(x, x**2, x, exp(x))
ax.set_yticks([0, 50, 100, 150])
ax.set_title("label and axis spacing")
# padding between axis label and axis numbers
ax.xaxis.labelpad = 5
ax.yaxis.labelpad = 5
ax.set_xlabel("x")
ax.set_ylabel("y");
fig
调整坐标轴的位置:
fig, ax = plt.subplots(1, 1)
ax.plot(x, x**2, x, exp(x))
ax.set_yticks([0, 50, 100, 150])
ax.set_title("title")
ax.set_xlabel("x")
ax.set_ylabel("y")
fig.subplots_adjust(left=0.15, right=.9, bottom=0.1, top=0.9);
fig
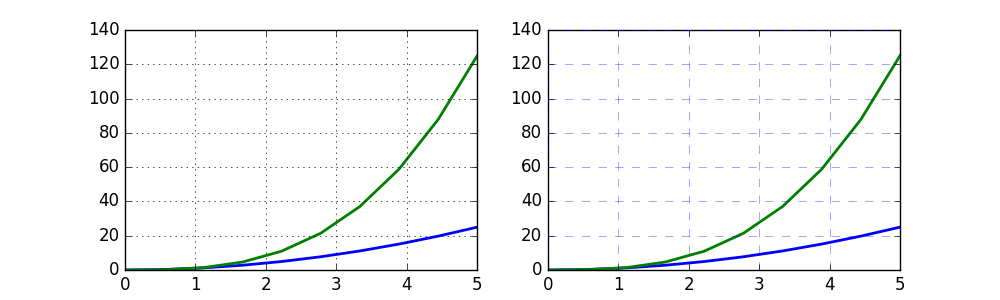
坐标轴网格
grid 方法可以打开关闭网格线,也可以自定义网格的样式:
fig, axes = plt.subplots(1, 2, figsize=(10,3))
# default grid appearance
axes[0].plot(x, x**2, x, x**3, lw=2)
axes[0].grid(True)
# custom grid appearance
axes[1].plot(x, x**2, x, x**3, lw=2)
axes[1].grid(color='b', alpha=0.5, linestyle='dashed', linewidth=0.5)
fig
轴
我们也可以改变轴的属性:
fig, ax = plt.subplots(figsize=(6,2))
ax.spines['bottom'].set_color('blue')
ax.spines['top'].set_color('blue')
ax.spines['left'].set_color('red')
ax.spines['left'].set_linewidth(2)
# turn off axis spine to the right
ax.spines['right'].set_color("none")
ax.yaxis.tick_left() # only ticks on the left side
fig
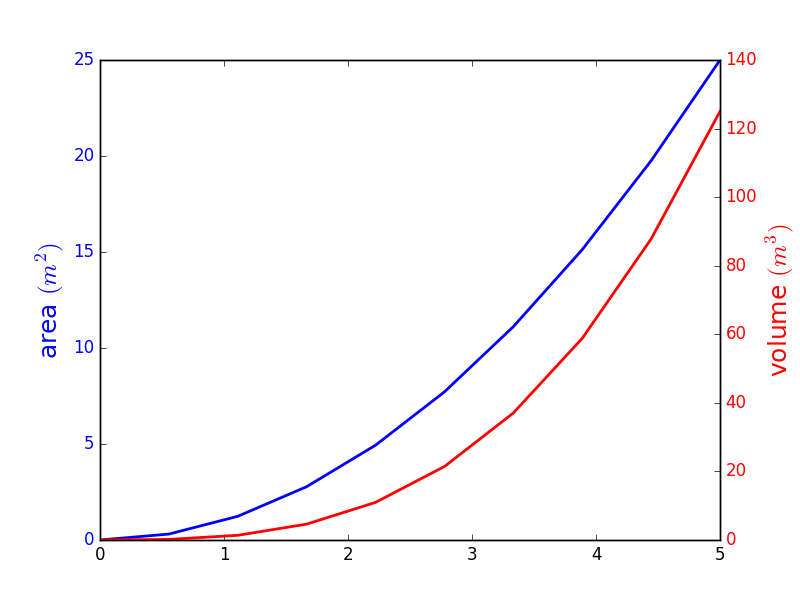
双坐标轴
twinx 与 twiny 函数能设置双坐标轴:
fig, ax1 = plt.subplots()
ax1.plot(x, x**2, lw=2, color="blue")
ax1.set_ylabel(r"area $(m^2)$", fontsize=18, color="blue")
for label in ax1.get_yticklabels():
label.set_color("blue")
ax2 = ax1.twinx()
ax2.plot(x, x**3, lw=2, color="red")
ax2.set_ylabel(r"volume $(m^3)$", fontsize=18, color="red")
for label in ax2.get_yticklabels():
label.set_color("red")
fig
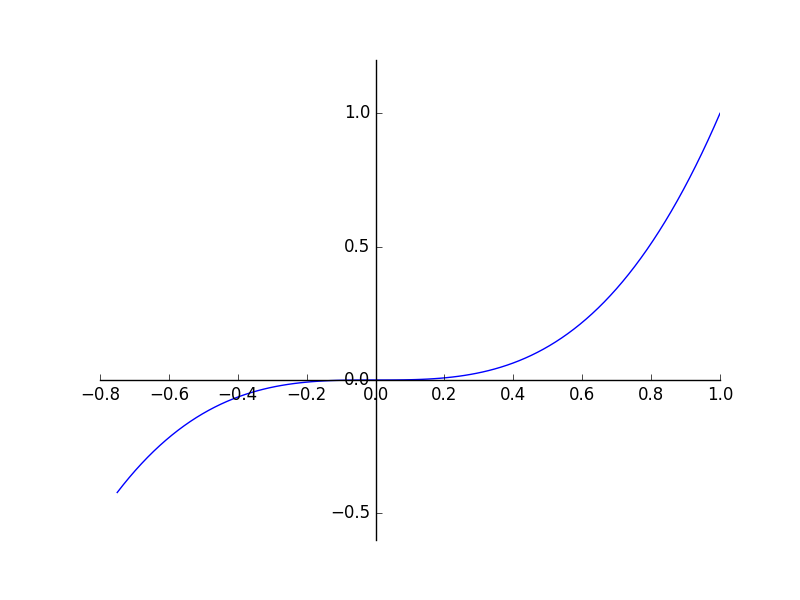
设置坐标原点在(0,0)点
fig, ax = plt.subplots()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.spines['bottom'].set_position(('data',0)) # set position of x spine to x=0
ax.yaxis.set_ticks_position('left')
ax.spines['left'].set_position(('data',0)) # set position of y spine to y=0
xx = np.linspace(-0.75, 1., 100)
ax.plot(xx, xx**3);
fig
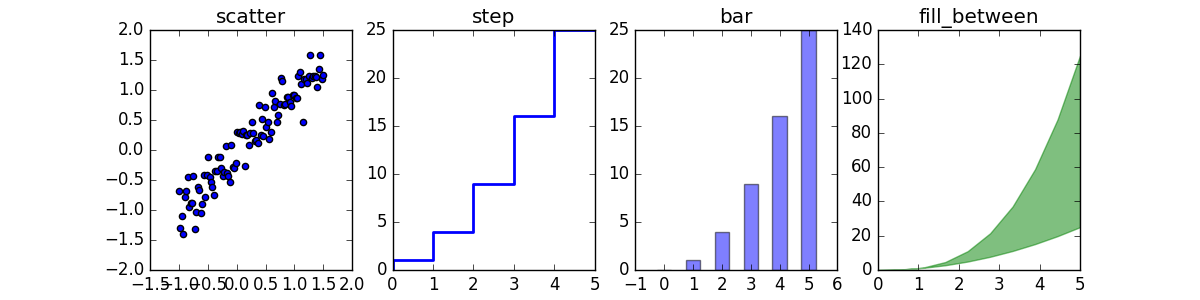
其他 2D 图表风格
包括一般的 plot 方法, 还有很多其他函数能够生成不同类型的图表,详情请见 http://matplotlib.org/gallery.html 这里列出其中几种比较常见的函数方法。
n = array([0,1,2,3,4,5])
fig, axes = plt.subplots(1, 4, figsize=(12,3))
axes[0].scatter(xx, xx + 0.25*randn(len(xx)))
axes[0].set_title("scatter")
axes[1].step(n, n**2, lw=2)
axes[1].set_title("step")
axes[2].bar(n, n**2, align="center", width=0.5, alpha=0.5)
axes[2].set_title("bar")
axes[3].fill_between(x, x**2, x**3, color="green", alpha=0.5);
axes[3].set_title("fill_between");
fig
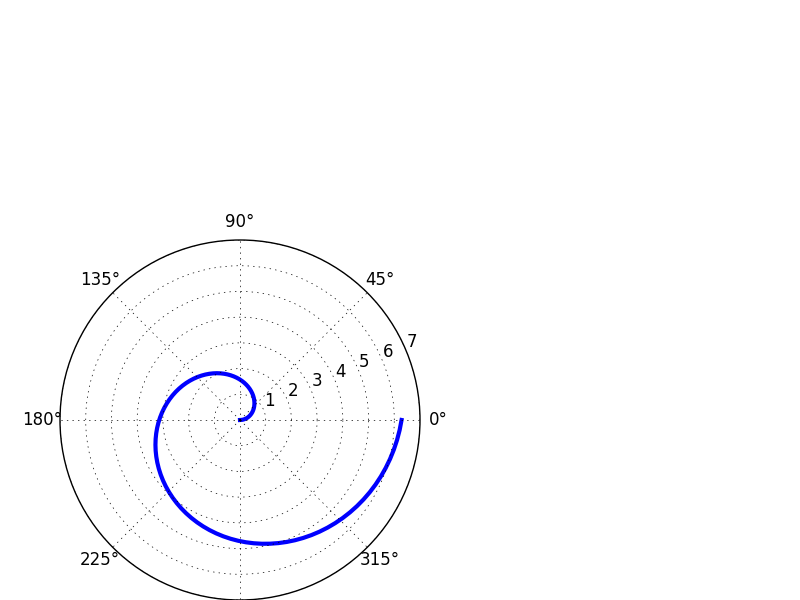
# polar plot using add_axes and polar projection
fig = plt.figure()
ax = fig.add_axes([0.0, 0.0, .6, .6], polar=True)
t = linspace(0, 2 * pi, 100)
ax.plot(t, t, color='blue', lw=3);
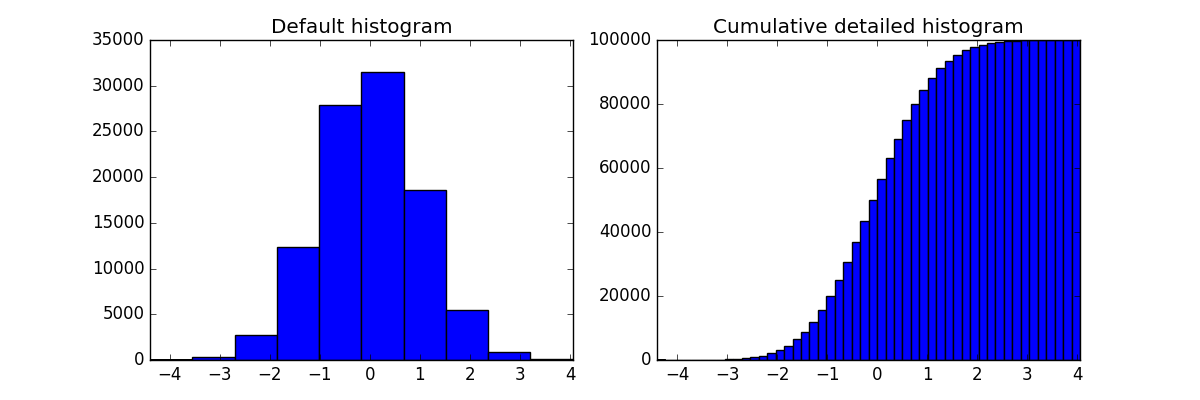
# A histogram
n = np.random.randn(100000)
fig, axes = plt.subplots(1, 2, figsize=(12,4))
axes[0].hist(n)
axes[0].set_title("Default histogram")
axes[0].set_xlim((min(n), max(n)))
axes[1].hist(n, cumulative=True, bins=50)
axes[1].set_title("Cumulative detailed histogram")
axes[1].set_xlim((min(n), max(n)));
fig
hist的参数含义
x : (n,) array or sequence of (n,) arrays
这个参数是指定每个bin(箱子)分布的数据,对应x轴
bins : integer or array_like, optional
这个参数指定bin(箱子)的个数,也就是总共有几条条状图
normed : boolean, optional
If True, the first element of the return tuple will be the counts normalized to form a probability density, i.e.,n/(len(x)`dbin)
这个参数指定密度,也就是每个条状图的占比例比,默认为1
color : color or array_like of colors or None, optional
这个指定条状图的颜色
参见:hist的使用
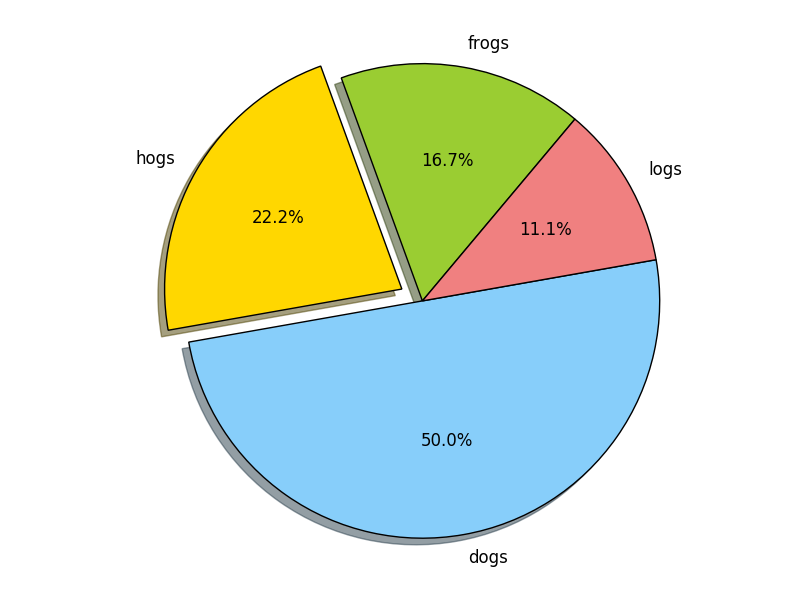
饼状图
import matplotlib.pyplot as plt
labels='frogs','hogs','dogs','logs'
sizes=15,20,45,10
colors='yellowgreen','gold','lightskyblue','lightcoral'
explode=0,0.1,0,0
plt.pie(sizes,explode=explode,labels=labels,colors=colors,autopct='%1.1f%%',shadow=True,startangle=50)
plt.axis('equal')
plt.show()
文本注释
text 函数可以做文本注释,且支持 LaTeX 格式:
fig, ax = plt.subplots()
ax.plot(xx, xx**2, xx, xx**3)
ax.text(0.15, 0.2, r"$y=x^2$", fontsize=20, color="blue")
ax.text(0.65, 0.1, r"$y=x^3$", fontsize=20, color="green");
fig
带有多子图与插图的图
fig.add_axes 在图中加入新坐标轴
subplots, subplot2grid,gridspec等 子图布局管理器
subplots
fig, ax = plt.subplots(2, 3)
fig.tight_layout()
fig
subplot2grid
fig = plt.figure()
ax1 = plt.subplot2grid((3,3), (0,0), colspan=3)
ax2 = plt.subplot2grid((3,3), (1,0), colspan=2)
ax3 = plt.subplot2grid((3,3), (1,2), rowspan=2)
ax4 = plt.subplot2grid((3,3), (2,0))
ax5 = plt.subplot2grid((3,3), (2,1))
fig.tight_layout()
fig
颜色映射图与轮廓图
颜色映射图与轮廓图适合绘制两个变量的函数。
aaarticlea/png;base64,iVBORw0KGgoAAAANSUhEUgAAAV8AAAEECAYAAACP/De1AAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAIABJREFUeJztvXu0bVddJvj91tp7n73POffeJEgibQxKISaghoCtMsRABboBbS0fXd0yNAXDwXBEGttKt8igR1ASEMThKMq2QdsmgjykUcpIKVp0tfIyWo2II5iQCmIRYgQCedx7z7nnsR9r9h9rzjW/uddv7rX2Pvucfe5xfmOcceaea+2112Outb75/V5ijEFCQkJCwtEiW/UOJCQkJPxTRHr4JiQkJKwA6eGbkJCQsAKkh29CQkLCCpAevgkJCQkrQHr4JiQkJKwA6eGbkJCQsAI0PnxF5BUi8kkR2RORtzese7OIfElEzonI7SLSW96uJiQkJJwctGG+/wjgdQB+a9ZKIvICAK8CcAOAJwJ4EoBbD7qDCQkJCScRjQ9fY8wdxpgPAHikYdWXAHibMeZeY8xZALcBeOnBdzEhISHh5GEezVcalj8VwF30+dMArhCRS+feq4SEhIQTjnkevk1JIDYBnKPP5+3/U3PtUUJCQsI/ASyT+W4DOE2fz9j/W3PtUUJCQsI/AXTmWLeJ+d4D4OkA3m8/XwvgIWPMY7ySiKQ0agkJCa1hjGkiflHM+7w5yG/Ni8aHr4jkALp23VxE1gCMjTGTqVXfCeAdIvIeAF8G8BoAqmvaLWtPCj5PlNMzUVJd8nq8XOvXttkGOZ36XibB/+n2Rl5OHD42fhTf2/8aAMCZrp9MnOnmAIDBJWtV3/rj1v33r6D25aU6s/61j6v6Nq98vP/dK54AAOhc8fVVX/Y1V1btYrP8/fGpy6u+s3v+Ej2669sPnt8DAPzj1l7V94VHdmrtj77r1/CkF/0EAOD8Y7vV8p1z+1X7wvly3f1zX636hhe8+jTaKdWn0e6239fxsGqbYnoYAZLl/hg73luxO9gs/6/7CVZv40zVXjtTnq+N0/68rp/x5/70pQP8lz/5LTzpRT+Br/+aDQDAE+l6cPvrTvUBAFee7ld9lw38fl3SL9udra/4fd1+2B/jww9W7fFD/wAAGD70papv+0F/vna+XNqyL3zFTxIvPOSvxw5dm92z5bk/N/Ln7dyowB/vPYzv7X8NtsdF+f1JUS0fFqbW5r6D3iu5SK1vVr+2PLbe6/f/y2I7R+g942Wt1ht+6m0H/q150Ib5vgbAz9PnHwfwWhF5B0q2e40x5kFjzIdE5JcBfBjAACUD/gVtg/WTrl19v472IA63p32v/eCKDRh93SN7MS4EaZGfObcvkODmyGYfVxY5bveg5Adm0/LYutrypu81LY/ttwMf9zzno815XiXCcVrf19jyRe4V7cHaZr/aPpAPiqbxtio0PnyNMa8F8NrI4sCYZox5M4A3H3ivEhISEpaEi/bhm9CMb+qsN690EeLSJ1+36l1YOk7iMQEndwwuA1n3eAbaruThW3OxUKcaPP+pT29CnVf73uxpFyM21fHTqtlToSMd+IXX8sT4Nrjtlove1mbUwfTbti/75mf479PyrOOvYGb7A52WBrsMS61YcpIHijlkB/5eltW3z79r94X3j/dbMqmOqZJeIvKC646dwwomcj2K+vU4TMwag9pUn6W8JomiaVttNN+2yw8j2UyWmG9CQkLC0SPJDoReJgFb1U4NvwG1t3Wc2dYNbvyG1QwKMYOB1h/u12xm7Iw9jrHNCzNhJlX3CtC/5L/Dv5opjKOrsF0A6Fnm2CMGmStsFwAy6/HBXgmat0LeGem7O1G8HYjt5rRdt62YN0S1L3xctN89pc3H3VWMb3zegquozDSisNcuuJ5zgMePZkAMmafd7wiD9Ww1+mvR78R+t42Hg98vfd3DRHr4JiQkJKwAi5Kfw8bKmC9D9/OttzU2HFs3pgk3ucVob+tezB1JYRFNb3OZxy9HQeAXG2i+5UGy7li6aLu2X9Wxp0xhuwAdN2untIGMjsExS9Zhma0Wtj8j397geLImP9+ub3cdi+7V+oJ9of3j/W46xoDRu1lLoPnSdp2bO8/G6Nxr/svzoGmchOOQZ3n15T26cYZFve+g90ds/OuzRH3dtr+/CBLzTUhISFgB0sOXMMizxgg2LchiYup90/2jhgi3eaJ53Fs4xrib3tyLsFxDVnJV840wXynGtb6MmC/vazeva76aHrpGfZ2erv/mVmft9Hwk2aQ38G3LeHPq45uhGNe14IDtKpovb4t/1+1LHtnvNeUY+bj5fLhzFDC5wMxQnufqvFNfeWCTWpuvp1nQG8KNqXysL/cMUw+c8ENydrBDuM3Zv9WdI8It7lk0ex8OguRqlpCQkLACJOabkJCQsAKkhy9hkAuacjeEBjOprcdSAycJyU19eehQ3n4/3YRUc+XhbTVtM2vxo0WDG1LlksWyBE/Z3ZSXprt55qfvvAtda/3t5lmtDwDWe+Vg7SnyAgB0un4wd+y62T6tu+Zlga6WOCfXXcWalnf7m7XtZ7xfdl94/3i/+XjcMfJxa+cjnEbTTrrjMpHrEchHs41vTde+afxo+9icQ2HmJsPfD743W0oIjdP170XPp7L9ZSEFWSQkJCSsAIn5Ega1V55jtr5HSxnZxn2siSXPk3Ky+c1eN8rkEZestmCjTMGMyTKpgEUFRp3SAsMGoLyjB1E4Y9IaMb0+scKBZYWDnh8e633fHu773xhZxttb88uLiTeCaS5Xk6FPT1koy5mpsHHNMV42svHvdmw6z+6a/z7vNx+PO0Y+bj4flcEtEogiY3sO2OBGx2KUa8fXc9GAi0wxBGpslF3JGNq9FEPb8GEtDWubdZvY+bKw6MNXRD4C4DsBuIv8oDHmmsi6NwP4OQDrKDM6/pQxRvevtDie3scJCQkJS4Jkeas/BQbA/2SMOWX/Yg/ehSq3r4T5bnT0N1ERsFWN+daTQgPh29atMyxmu6U15QhmxN7Qjl3E3vYHReCOpLiamZF/sVbBFcx82b2M9rFj2wHrU5jvJrFKp5ECwDZpql27zoSY3GTCw6pM+BLLu9uUTJ31Xcd4u7Rf3X59X1jz5f3m43HHyMfN58OdIy3kGICfabDmS9dDdTVbYrKdGNvUZnbh8nl+YzZbdeM/fn9os0R9W015lw8Cza4wB9rsWFW5HQBE5DYAvwPg1TP36yB7lZCQkHDcIXne6i+CN4rIV0Xkz0XkOZF1FqrcvhLmu3YmfBMVyuvYUN9kOKn19YhF8NcdI+5lzJJRWzfmDaFhHs2L1xWrIbYJtjCVpqsHWTiGGLOow+qJMvHMN6NKT6G3g9V8I3rnwDLHgDX2vefEVt//xtiWs2G2q+WcCVNS9mjdBubbqXtZrA38vgQs2Gq9A9J5eb/5eNwx8nGvKQEXfN74fFbnWdF2gfA6GS3IYo6ACx4/bkzFw4vL/lj4cHOlitnePBqbjc382JOkCg6ha6DdFzU7yZdqq8yNAxjcXoWyWs8QwIsB/KGIPN0YM13baFbl9scQQfJ2SEhIONGIPXz3vnQP9r70mej3jDGfoI/vFJEXA/heAP/H1KoLVW5PD9+EhIQTjdjDd/B134bB131b9fnc3/y7RX+iVeX2aaxGdji9Fnx2skM4LfPzo8JOI3l61iEtwckSANCz1Vtjxjm32UWrt2puZzHDgTat4j6j/HARye1QHTtX/qV2NrHtiZ/usttZhwIu3OyaDUzrbKSy7U2evu/59il2O7PnOyyqoRRspOn9JDiu+hBkiSJXgijYlWyNZAUnR/D+sZGNj8cdIx93aHBz/+l6FiT52PMsE38NuCpzcJ0USalQpAYeDzGpyvVnEVczzcUsnge7Dn18o9bH6wa5PkhWyGlnqiokuX5/ODllEffMJmTZ/NsUkTMAvgvAR1G6mv2PAL4HwE8rq7eu3M5IzDchIeFEQxZ4+ALoAngdgKsBTADcC+BfGGM+JyJXYcHK7YxjwnzrLKAgZuuWT0bEfPvMfKltDUAFseEuLR9ZxqG555Tt2fvemO+X3vbuLS75Yk4lzPSL4bjWFxjfHBMjtivEgnuU2aln96eX+4NlBuiMUWfIsLVL53N35Nv7bqYxpv0y/ntu4DOjYQNrobDksFIGuci5sGfFyAZ4Zntm3R/rJet+X/h4Bgrz7XEocnWOiJ2NlFkFnePQyDb72s0DHj9VkAWNs96+Vhret9m4rKEp8IENZ8H4ttcj70bYLu133nXMlr9fvy+yBe+VWcgX2KYx5mEA3xFZ9gCWULk9Md+EhIQTjQWZ76FjJQ/f/qV9Nbwy0HnZ1WxUdzVjnTdoW3Y83iWXqx65XNl1g+0Ta2tK8qO6mnX0t72mc8XgzkcYXjxb88W4zrpYg8Ror2p2ehtVu+uCQ2i/mAGesoxmd1RnlQBwydAzyInCXLcU5jqm7Rd0vgvlfLOemQWuZvVQ5lPEbB+3Wc6oLiGGq+m8gD/GkPlyUIr9Tb50dD7deQ5mH0G7rvkWMVezORLruDEVsMoOuWBWNg///aZKFQHb7dRZdsY6LidVGnRsX0zzrbuV8fdj+u+ykR6+CQkJCSvAYUbPHQSrYb6XDFT9K+bt4JhvyHbrOi+vw29j1oqdFhx+R2ch3gtDF4Iry3PkDb5YYh09+UqlG5LuaPZ3qV2yMhmQLsmeD+P9qt3Le/a/3z+29G/aBDQ7dI5GxCaHxFzHlvkyA+YENNt2u0O6dkVg9W/SfEnb7NW9ME7165ruGWLDlzIL5qARe4x83Hw+XJvPG59Px3LdeS/bdD3oOlXXLhjfi9V483aE2Dizsy0as11aqo9ZXdN1LDVkvjQTccw3woyDbSn6sObtcBhIzDchISFhBUgP34SEhIQVIO+kh2+FtUsDLw0yNtGUW3HVmYzG1EdT4r16/4imQixXOENcNuKpEhvseHo8W3Zw4OmTNq2SyDSa4X4jOG463omdxpogyIIkiGE5/c3I4CaRdm+tDwDok6vZkAZoFWRB+W9HJA+MFKmA0VOype3QNWDZQjPYsWyhVZ/gfA0cRPG4zVJOuWyjpy7n43HHuEbH3Q9kB2vY2p99PoshyQ6BAdSv664dX8+wUKoivQSG27qsxeOMIS3HahYZs5rE4OQFIJQYulb+yZS++rbcun65BLkfcvt/+fKDJM03ISEh4eixSITbUWA1zPeSTbU/MDAFLFdhvmTQyHeJZeyV/fy2Zrczx4g1NgyEjNjtDxvkmqAZMuZxHI9mvrJtPi8Zsy7bNtQnXWqTm1TeKV2yerlnkMz6xtZQMqLQX3YJ04xkjKBEuz32QY+ZL800GplvPfgjCB+mtmO8Z4jtBm1ad8MeY18xsgFAPikNbXzeuK2db24HLFdxI5ynkkXAgqsxxeeNWDBb1xQ4I5gWAAHoLJfZbLDcXo+cZiKdgZ91ZF2qIagw36xLLDgZ3BISEhJOFtLDlzB43Jngc8XqGjTf8R4lMSFmkfeZ+ZaMZUxsOO96lux0KGa7rGNxf+W21tODPzT2ooWCtnEgLxrYkTveCZ2DnConODcns3vB//7aut8vdpmy7bW+D/Mmb7xK0z3Fmi+7/inEl30pe0pVDA5P3p9D89UqbAzoep0m1uUCJ7iPdV4+njVXxy5SzUPsONLOGwAU9jyH7mU8DutjNXptG1iw6lbGAQwtxyHgH0Q85jU2y/3MfDWWm9M46vSZ+XZq/THNNztEzTf5+SYkJCSsAIn5EnqXXhJ2VDWudObrWER3SBUU9jwLyfeYcbi3se8bX/DsJOuV/axzjclbgsX5iaIPhyHQLp0ipQJs8GxoYsHMgljjnjjde1j3cOA2W99lf8e3O56diNV6s9yzlD4tn5jM/vf7cslAHyrucDpK5V8A2F8rt8HJeBb1dqiqTygBIYBnvtzH+82eDQN7/fvUl7G+O9wJ/gOAofNZNGi+fJ0mms1iDrbLcMxUMmLRCrMNdWJO/OSCHXSdtxPou13b58dJZ4Nq6vXdvdar9ZVtP6Yc4+V1A28Hl3P3EMq8c8j0cULjXonIZSJyh4hsi8j9Npt7bN3XiMg/iMhZEfmwiDx1ububkJCQMB9EpNXfUaPNK+EtAPYAXA7gxwD8uvZQFZEfAHATyoTDlwH4SwDvWt6uJiQkJMwPydr9HTVmyg4isgHghwE8zRizA+BOEfkAgBtRL4v8NAB/boy53373PQBu1rabX/p4PbepkgkKALK+lQ3Iib2z72UHNm6MrMTAUkROwn/mlndpeY+c59kFxwVsRKpPaIU9GTKHwc1JF6HzPQV82ClrEHhBx5gN7DSYDG6m1/fL2fg2Ks+BUCHLHk33Jtb4MYlN19hAY1dhowaXW9+302vOHjaaw82qqxS45KKXQaYym9v3FJeIZ9mCy8Tba9IzlP94RDKNO0eKkQ3w5zmQGiIGYW9w02U1rfIHQy00ybwpr68bK1SpBUb0NsiIRrKAkwi6LDVs9Gvr8nKWFfI1ytvdKX9D1vy6LDvgYOXdZ+K4+vk2Pe+fAmBsjPkc9d2F8kE7jT8F8CwR+SYR6aKsZf8ny9nNhISEhMUgmbT6O2o0Gdw24csgO2xhKos7UFb6FJHfBnAfyrIbDwB4nrbR7Mzjwg5X44rLiI/r2bs4fFOIceTESNybd3zBLx91647dox0yrihO7AAw3rU5cok5cMCF69eMcIw2QRZaHTst0ITd7Trcttm1zJ4/F8WaZymyS21raJPcGyKR+XPUXysvb0jI9GPIrFc/VzvgTGF71rgWhCfzMTbk82Xm6xh1U+25wLAWMN96KLGQq5gMqT0qGa/Z9QVoCzq37jxzVjNmvoFb5LA+a9Gy58XA46dA+b3Q/Uwp0R7JLuYMap2BznbZoNZdL8dMl9iuxoKZ4crA540WmnmJwnwdGwbY4Hb8wotF5JsA/C2A3zPG3KgsfymA2wHsUPf3GWM+Nmu7TQ/f6ZLIQFkWuVYSWURegfJheyXKInI3AvgzEXmaMWaX173tN99btZ/zzG/Bc67TiHRCQsI/NXz0r/8WH/3ru5e6zSXIDm8B8AkAs96Sdxpjrp9no00P388C6IjIk0l6uBaAdnZeCOC9xpgv2s+/LSL/FsA1AD7FK976qp+p3MsYQWISclh3LDhIYhLRNsUyEnbwDhy7XcIUdkLPdObrK1H4vlFObmmWZbArmladOGApNBCY8WRT3ynbdbezPOZut1O+3zrMJui8FNTObZsZZkEWh8y216n6BY/fjNbNpdzHTk5VgMmNaTguj2ef9M5RU6E8Arutrdnf6BGDDXLwKsxYY7sAkA3LcSL7FJSyv121xS6fKDov4PXf8Y7nFXw9CrpOEzXIQqlczeOBxwmt47Te2JhyWm8s2Y0LkuAw4O66ruk6xts77cdBZ53sCJblSj/CdokFZ66fxyfVFXTM+IYbnosbbnhu1f/6t/3fOCg6B3A1E5EfBfAYgM8AePKsVefd9sy9MsZcAPD7AG4TkXUReTaA74fuxfBpAP+DiFwuIpmI3Ijy4f45Zd2EhISEI0GeSau/aYjIaQC3onQcmPVwNQCuE5Gvish9InKLiDQ6LLcJsng5gN8C8BUADwO4yRhz73T5ZACvB/C/o3wIDwD8HYAfMcZMa8Yo+qFkLM6ZnyzAQszYpe9jnZfZbsCI3ZuVrKfdjmcsWg2saLtBfxopfZzSz2Ttrfo+xFoPsshsIqFAVyRG7/TfvE/JXfZIguqwc7tlR+ThwOy/sIyYj75PLFi0CrdcOSGjmmI2AcygoMoipPMqki9Yogvqi2Vu+3W2W/6WEjJMB+HYLgCIZbnZkNjuyLPYYuts+f8Ca74UcGHHXEznDT0f7LWLBFk01nALpx3lvkbChzMlGQ6HBDs2G/NgYH23d6q85p1NnwgrYLP90oNGNrwymUWYr2PEhgJ7OKDC2PFnDsHnS3uwtsTrALzNGPNFEZk1XfsYSo+wL4jItwB4H4AxgF+atfHGh68x5jEAP6T0PwAyvFlXtJc1bS8hISHhKBF7+D5836fw8H2fUpeJyNNR2rCuc12x7RtjPk/tu0XkNgCvxEEfvgkJCQkXM2IP3yuueSauuOaZ1ef7/vB2XvwcAN8A4AE709sEkIvINcaYb2/xs410eyUP36IfZjXzsgNJDQW75VjZoRMJGmB3IEV2MCTydzTZ4YDuLZPAFY0Lc9rfnyOogB3uuVpH0bX5AbokRSjBJWxc7GZe8TEsKzjjGJ0XNqKJa5MmkFGeh36XnOqtYbPDUkNQ9aL8P+bjYtkBdQTlIEl26NibiOx5VR/gZYcuB06wKxkZ11xABbuXFRf8+Sp2yjFldugc0vKxdVUcUd4QlhomipsgX8+mwIoY3LjVilMCeo5dzVWsE8gL/l5i41q+UcoNGckKbFzLNsqJb8bywsBLiiwxVPcl9Rlyb3QSxGHIDp3FZIffBODcsgTAz6J8GN80vaKIvAjAp4wxD4nI1QBuAfC7jfu1yF4lJCQkXCxYRPO17rHVm1VEtgHsGmMeUexdNwB4u4hsAngIpUPCG5p+YyUPXzOYyufbwHxd2HFYCp2CJOgN6tyoOHS26M5O77/MwEZ2F3IveSr9FYVzPeLvc+Yqx6SE3JkCo4urFEBMjBl9h7NFNTi0O5ZrDAdDEHuna9PtlqypQ1Uxxhyo4krLG3KdItJnFIsbG/SywPjmjoXYMDliVYZZDhMmZptxv2XBAdvdPuvbtp8NbuxW5hjvOGpwo/B3FxoeCazQ3M5ieW31ShTEfC3jbQqMaGK7gGe82SmfhTBbJ+OaZb6GZkJFz7cNzVRNrsxIFeZ7GEkWuBrKojDG3ErtaXvXK1FqvHMhMd+EhIQTjQN4OxwqVvLw3TXhm0jE5vqkveFqz9KxjGLCQRikVypv0Cxgeu3fpl12AXJhz7G6alVYtO/L2VWs2iW9Egaj6h/Wg0/KbZT9k4z0zNyzq3GDlh0wqabzYY8no5lIFiSFIT3ezkpMl5gW6Xpdy3gMXVxDzLbJ1UxohWo2xGHmXFHY5uMNqk9wyDC5mjlGW5Cm69zLyuVl/2TXs2XWd0c2fJ3D2AO2O2TN1147KhcS6PmN4cX1uoCcjzcLqlKU555z6XKyG83VTGO7gGe82eYl6nLHeE3Ps+iCWDC6debLOvCYDtudAm0mdFCkh29CQkLCCpAevoTtqWrA7uQw42FH+k5Wvi17lMAjI42xIFbl9F8OGsjm0JE6RXvmWzQyY5ssh53g6bc0xhNovkHAhc6Iq3UV5htDo8ZdKBr8BqX4ZOZrU3ManpXQtXG6nvC0hq+Hdm1YX+b2xOre9PuaHcAlxQEA0+DNEPRRe3KhDL4YnvdsebjlWbBjvBxSPFaqaAP+2s2XTIfZbr2GW1CDLUgDuWb/19lu2bbeDpuz2S7gGS8zX9NjfXez1hfov1QdZWiPdzxmT5h6sI1W2eSgyFMNt4SEhISjR2K+CQkJCStAevgStkdFIDFk1q2eZ8w8VXDO8+OC+2haRZULnPGtoO8LZ+xS8kiEbT/V7hbKdFGpUFAo+YIBIFfcx7iaAUMLxGAXNc0V7aBg42JHOQecWS5jI1ffG1iqzFYdmuqz7OBci+gaBC5GDQhcDu21E6p4wrIDrKEtqDhB+RhYVnD5eANXsm2f58EZ1zSpgZePAoOb35fRXt3gVkQy1lXHEpGMNLeyLDbmXNALZy3jHL2b5fVybmJlm2SHwJWsbBdr3hXNUI4Ps1bKDmxkG5GwNiQDo5MdhlwJhoxr7nQUM7M2Loa1Y1pAMzHfhISEE43EfAln98YBs3UhpJy7lR3phxNbb4tzu0bytLrsW7F3nQscYDcqZrvM9sSyvZzqxXE+U60keK4wYzaexAKNC83QwPs1qQ8gLataDBrTMopxEfCMXzi/MrUzpVx6kMeVqhVkLqw0Y1ez9gY3UYI7eF8KCh92+xKw3d169QnA5+Ydbfs+zZVsdJ6YLxnX3PImtgv4kHP1GhPySCyAZnzLKYw86/mZhjO08TgNyrUrOXizdWbBFB5sGa/GdgGgsP17xGb3aJztk3HNMV42so2D6iZ2ZpdczRISEhJOBtLDl/DYbsjZNOar1ekaBTlh2VGfksbYF2dQhSEIky1XyILcweRGpbC9fOCZXkepHhzkbiX9raqakeluQ0YJqIhVQp44ZkBsIVc0xI4SBDLdnv5OrN1htkszAq7Ym1nmGa3N5Wp3cXXaIPijTveiVX5dQMeYdd56rb8g7y4xY+53+q3GdoPlO5HldgyPie1yfT92DYxdUwdfC5DGJFdfCcaPra6i6LyAdzvrDCjIYkBJqPpO86VkORw4ETBb50pGQRR0X+1UVUr88e2O/THsBcy37N+h87JH6ybmm5CQkHDCkB6+hId3RsjZ26FKFciarmdE7g3JlWonFKLMUlphWTCf777CgjlENptELPlOQ+RKydy2LIM1NU6u4hhJEQkZZnhvhtl1vrQacWU7q/cVunXdtSeKPs3tydCfl86AKiWvk+arMF9RmG9QSSMmbioIvEMU5mu0Ktd0jcY7zFb3a/2jwIOhHiocsF1iueNdd45I2+Xw4Tmuo6vLhshDIgu8HVzQCifT6dXams4LcN01YsNB4ITvd8ETzHb3ApZr7P+C+nz7Ap0bx3h3RqwJU12/oj6zWxZ6ydshISEh4eiRmG9CQkLCCpAevoRHd8MEtz07rQplB56eZPZ/3XAGAMbUDyOozEAZoFwVhmJCzvsUzcBZ+Ss3KnJXyoIS7Hv2v278mLTIszANE8nz6qaxPAUtwNPcsp+nbcVEb7vtchl6nt67ygucq4DzA/D0vWONkXnfG7Mykh2c8S2QGrTcwoyYG6DbR3Y1o7YzfPL+TYJqH3v1dRX3sXJ5ud2RIjUA3qDGskMxrBs1y0OoX7sAc6Sb9VnNOIc1t8vzHRSy5LaVG3iccw5eDphweRr2yaCtSQwsJWzTmDpH566t7DCco+pLW6TcDgkJCQkrQJYevh5fPb8ffHbTggFlauL2/ti5mnFoov8+vyxdbmCtAgIA5N3SENFlwwLlf+WsTI4xhAEEdef1INSzp7iaKflYp+HYEbMBaFWLAAAgAElEQVRddldyzJWNOkHwhis9z+5OPTYGMUMr2x3uYxe6fskKOxSWyssDA+POXq0vp8oh7nzEcgtr56Mpf3IxZAZaZ76cSzdW2n2sVqKos9xR4EpWZ7mFksWu7K8bjnh5TnTXbYNz9IbnSHE160XCi+114HEqCgvmcR5UnKD7YmSzCe6PdIOaazPDPbfv28yCt23/BRpzu8N6+3Cymh3s+yLyTQD+FsDvGWNujKxzM4CfA7AO4P0AfsoYM7OGzfE0AyYkJCQsCVkmrf5m4C0APgHoiSdE5AUAXoWyltsTATwJwK3auoyVMN+vbIXM12m+7BKyTsx3t1/uJjPfmEuKIwwZKORSiHHYKrsdyjUa5COl2nBOF+NwVQ5RreqmcWAFM7w5cuw6xOt81Zmxpo5xVYNsRMx4WHd9mighsNyeBGzYM9sscOpfs78bYWKHwHyDKhFKlWDWcXl5wHKVIIlQ0y2UvvpMpI0boWOuBXhs0AymgQNp1Un4fGpJdpjtZoqrWdGNjH+6L1zwxC4FS+yOfHvLsllmu+cp3Jr7z9nzvc06MJ27oWXRh6H5dg9QnVxEfhTAYwA+A+DJkdVeAuBtxph77XduA/A7AF49a9uJ+SYkJJxo5NLubxoicholg70ZwCxq/FQAd9HnTwO4QkQunbVfq2G+5/eCzy7lGzPfzb5nru6t2EYPcieR33ZcvLRXJenxy3useXHb6mKaZsbtvEeWfiXhibR48zo2GuiGSp0vDrdlZuz0X2Zn/Lu5ov9y1VvWkl2YLLPCTp8DLvy1cZpqyHxp1lEFBcxmuzE0B4eQ54OS6GhMoexaKHCc+da9GTh8WAvX1q4HAIj1ROFaflkkWEZDwHIrb4a6hwMQsVP06mPaRMZ8kBLSnm9OlsPhwU7rjbHdRy/4mca5nXKdLdaE6XvuHmePpmWhQVKYhdehZLRfFJFZF2kTwDn67HKXnkLJmlUkb4eEhIQTjUW8HUTk6QCeB+A61zVj9W0Ap+nzGft/S1m3Qnr4JiQknGjEvB3u/qu/wD1/9Zexrz0HwDcAeEDKh/cmgFxErjHGfPvUuvcAeDpKLwcAuBbAQ8aYKOsFVvTwPbcdemDkiuwQiPHrpbFnHJEd+M3WsVPatY6f3nAm+z1r6ODcwF02vlG7ChBgt51ur9aOZZjKFLkha/B7iQVG+CKMer4GbbLG0/sJGd9yO33WpAjAT7W5SCNPyTs0VXfrsITBRj83Zc4issM8BrfKHY+ll2H9GFgq0IxovM444krmJIZYdjItP3JwDMExuu+xe1n7AppBf1YPsggMvnZMBuOUxq8b0yYy5rnSxF4lBZCRjYydW/Z8bdF5Y6nhEbrPncHt7I7v21UMbpPDkB0izPfbvuO78W3f8d3V59/7jX/Di38TwHttWwD8LMqH8U3Kpt4J4B0i8h4AXwbwGgBvb9qvxHwTEhJONBYJLzbG7AKo8omKyDaAXWPMIyJyFUq2e40x5kFjzIdE5JcBfBjAACUD/oWm31jJw3d3exjkKHWC+IiczIdjCtO1jDdmcOOT63ICcz7gPrHgnq0vxm/4NTa+dckQMbTMNmZw69SNHxqri4aVEiqDWyQfr1YHrIklZEL5YTkgo3Ilo8xYwzorZObLzHbUwHzznnYOyADF1145N02BC3yOtBy6sZBfjd3HcvDqdddoXxryzuadunEtNLLNznrG0GYNPM6C8edma5ExW7jahzTOx4qRDfCuZkGwBJ1b1//Yjs52mQU7xsuuZiMyvo3trOQwspp1l5DbwRhzK7UfQGlM4+VvBvDmebaZmG9CQsKJRgovJuxPVbJwmu94SBrleDbDy4MkPP57Liy5T8yA8wBv9upVVLnd5cq7liUYqpQsQdIYy4w5f20DS2mCiWi+VXgxnYthEG7dwMSoBlzljkesb5wrbJYYbEzTdSGxzJKZZbv+mLtPk+bLcKyImW0Qjl0x+tmacLluEXxnelsjF9DBYexN55grbgdj1iY9irDoJjSNqUwZkzxOefz6MU2unJF7wbWDxDnEVqsgix1yNaN7m/VdZ+cZ7VMyHdrWZHJ4mm/KapaQkJCwAhzTZ29zhJuIXCYid4jItojcLyIvnrHuk0Tkj0TkvIh8VUTetNzdTUhISJgPuUirv6NGG+b7FgB7AC5H6XD8QRG5yxjzGV5JRHoA/iOAXwPwLwFMAHyztsG9nVGgwzgDTIemuWG+3rK9Ra8wnkr0FNlhg6bJHJXj2gP6DruwmR5P0VzZc5pSr9UNbrycM3ppkW1sbApz72oFLuvSC0sNmuwQm80G+S3suR9SrlyWJdyUOScZKCNZIlMMcZqRrfxeud0mI1sMmvFNy3kB6O5hWpQgoJ9PlhXcqlofI8iYF7l/q/MZuThVRjraF4nJNJWrGUkNPD4V90he7sY0SxFjkp9YdvA5eOv3D+DlhrMRqWGL5IihNbQN9yMGt6FzI1y+we2i1HxFZAPADwN4mjFmB8CdIvIBADeinjTipQAeNMb8W+r72yXua0JCQsLcWKCmwZGgifk+BcDYGPM56rsLwHOVdb8LwBdE5I8B/NcA7gbw08aYu6dXHO6OwnLY9s00mdAbmoigexsKvcG2gwxo/g27vVYe0oV1/W3tYsc5QxrZE0B2PvSs8cJw8cdOPchCusszuEVZnWVg8zBfboeszNT6AmORvTY5/X6P3fkUQ13M4OaZb50Nt0FwPlw+34jhyhnPNMMZMH2+tL7ZLFc7n22Yr+s3kYx1TWgaU8H4c8EVNE55/Lp+Huc8/vm+2K8qVfj7h/PxOrcxztHArmT7u9y2lUHI4DYMmK+9dodQOv4gWc0OE017tQmfJMJhC1M+bhZXAvhRAL8K4AkAPgjgAyLSVdZNSEhIOBJkIq3+jhpNzHc6YQRQJo3QEkbsAPi4MeZD9vOviMgtAK7GlPwwvLAV1PTK7Nu4mPjd0bSfnHTHvY4/WVvEujb77m3s1z215rfr3uLsTD4udP23m3XcDlZ9otQnCzS3Bec47nhjWcs0DbKJyTUhxtrcNpjt8nZ7GenHLkscuQgFer4SYMCYy9WsCrLQgx3cPjado3Bd0PLZzFcDn6NQV+ftSrD/QHidF9E5g/PGdfCc5suuZjR+XZvHObeHSgazHYXtAt7VbIv69kj/HQX6brmN/cjyybhsF+OZxR8WwsUqO3wWQEdEnkzSw7UoJYVpfBpAFSgtEn+VnLvrDyrZYe1rr8H6ldfOtdMJCQknE3tfvhf7X753qdu8KA1uxpgLIvL7AG4TkZcBeAaA7wfwLGX1dwP4X0XkeQA+AuB/BvBVALUzufHNz4fQ23p0oUyFWawNaC1fS8o9qJk9dYjt8tvYJevgpB2cI9QlC9mjvlhtOMcomDmAqyK7Y2Dmq1RsaJPPV0OgZyqar8bkYsxXCxBgnVf3hqj3AVPM1/aHDJB+Y1If+PPU1NK11yY2y8x39vdi22o6XxqaZgrzBFYwGsdUMP5y16j6gvFrl/Ou8PjfU+4Vvn+0umt8/41JQGZN17UDNkwVYib7ZRqFzpmvR+fM11f95+/6AxwUx/TZ26qSxctRJov4CsoH7E3GmHtF5CoR2RKRKwHAGPNZAD8O4DcAPIryIf0DxphxZLsJCQkJh44M0urvqNHo52tzUv6Q0q8ll7gDwB1L27uEhISEA+K4Mt+VhBeP9rYD2SF3Ll3k9M+QrCz6l5NyPux5Qt1d89vasm4vW3ve4LDLrmbWoDBSpvRAmDmtCrhgJ3XF+BYrDjlPMIFDETEm+WmyX1dzO5sn3wMXY9UkiJgsMSxYgqjvi+bCdtDy3UAbqaC+L02ywjy5G2LnSwMvd7/B13MeVzNGprma8fhz+XoVqQHwwRVBNjfaL74v3L3C9w8b19y9Nh7p7mNaHgeWGsa721XbGdomyeCWkJCQcDKwCkmhDVby8HXiukNhmW9OBjdmxmPnGE4hw2OuVjCsGwTYZWbIxjX7Zmfn+0lglPFtY9mLIeMFGzKgGdyU12zgVhd5DWtuVCFrm83UNGMTO2w1sbqRqbO6rIEZl9sVZTnU9qy+GOYxuDUZJbVz08x2PQK2W/0WL+ffYuZbvzax7HUOYQ7fvLY86mqmGdyCtg1o4vMSBFnU7xW+f/i+cvca33/BfTnie7RkyXzvj4e+7foPw9UsyQ4JCQkJK8BxzWq2GuY73AuYrab1Zlk9CGNMJbLZpSXQnOxbWnOJAfybvY3m69p5TqeJWYjT2rI6MwEWdzHT0NY1ajSH61QMWuhsyKLrbc1VbbpfW94Ebb+bAiPasH9t3SY0MXqN7U73HxTqmMqUMcnjlMavVhUmpvm6eyV2L7l7LWC4kfvSMduJwna5n4NPloVFz76IvBtlBeMNAA8DuN0Y84vKei8FcDvKQDOH7zPGfGzW9hPzTUhIONE4QJDFGwG8zBizJyLfDOCjIvLXxpj/oKx7pzHm+nk2vpKH73h/N9CxnLcDs2G2euaVJZRCb6k94QQ0LlXguP6GBljzjbBd1nxdI6KfuWMIrM2HwHbL9mzNt5jxnVn9GpqSxmiMOJ7ER+ub7TUQ278m/VfTcedhyRrC/eN1614cMbbblO5zEcTGnBuTMTuF24VQ82W2W2fBgeZL95W71/j+C+7L4H6tezMUQXtUW74sLOppY4y5Z6prjDLeQcPcv3JMnTASEhISlgMRafUX+e5bReQCymrFrzfGfEpZzQC4zhaQuE9EbhERXYskpIdvQkLCiUYm7f40GGNejjK74/MBvF5EvkNZ7WMoc54/HsCPAHgxgFc27ddKZIdiPIQUivsMyQ7FqD494WnKZNKl5ZwJzE6FIrKCc3QPAhhI4w8c4V1TGt5RMYPbAt7dsYxeGnRZou5+Nr1u83ZdkIXva2rHjHNNv68brvSV9e3OlhIOmrWMv8P76oJLwu23n3nOc50Z6piKjD//Ja4Q4/63Gf+KcU6pvhKTAAtFYgjva5/hbKIsXxYO6mpmyiTDHxGR30P5YP3E1PLPU/tuEbkN5cP3l2ZtNxncEhISTjRiFOjOj38Mf/HnH59nU10Aj7Rct/GRv5KH77RrmXvbFcx8x93a+vw9zoFaKO2mfKUaGwZCk4qaVV8LsggWNzjEz4FmVjfbDSu2rfaYbWzi7Tay5Aj9KObYryaj4yIBGfNACxmO/1bd+LbYNYgE7sTYrhJkwXBjmvckZMH1eyV2L7l7je8/E7QntbbGhgH/DIilGDgIYnrus69/Dp59/XOqz7/ypjfydx6P0s3sD1HWsHw+ytqUz1e2/yIAnzLGPCQiVwO4BcDvNu1X0nwTEhJONBbUfA2AmwA8iJLtvg7AjcaYv5rO6AjgBgB3icg2ygo+/w7AG5r261gwX4dCeVNyv5lwH71hmblaySmmU1Xfb2CQ5Tp2m02a7zFAU82xNv116GxXcxULt6l97+B+Vm0rCi9T8w1dyer93Nc9ppFURtF8GRNF5w2WR+4ld6/x/RfclxPlHlbua+4/DOa7iKuZMeZh6LUqaxkdjTGvRAsD2zSS5puQkHCiMaOozkqxsocvv+Gi+tXUuvO8FTW2O6u/NTQW3GRtPgEIZwd1FhwLGfbf05fr3g5t9iG+/KDa7kUHbfwtYbam3Svz3D+a5jvPd5aFlNshISEhYQU4ps/e9PBNSEg42bgoC2gmJCQkXOw4ps/e9PBNSEg42ZBjqvuv7OHbZGTT1p3nO3lEZY/1t4ZRwkIPwUhw3BCvVNGultk87j7xdWcHK/h9mR0QcuKgjT9tnM4J7V6Z5/7h+7XtvTvPPd56P4rjWUA9Md+EhISTjSW8iA4DK3n4Sparb8Us8qZ0/UEtNHoDsx+f87DhN7T2ts4CJqe/zd3X5BCy6y8bTTl0m/Lt6ttsz3Zjy33inWUIb5rbWj1woikHb72/HQ5aj25VEHr4aOmm+XxpxqnYveTuNb7/gvsyV+5h5b4GwtQCS8cxnfEk5puQkHCykZivxzTzzbplJQtXq226rWm+kulvW9fuUB+3ezZJCb/B+W3P7301MoYvpKK1aU7ii6YPbGKQ3B4pCW5Ctjs/RWtis9zfxIxjLv/zVLKA8ltaPbmmgJB6//zQWbB+bQ7K/rXxEw1GcP2RB44b07wnwSxQuVdi95K71wK2G7SV2W1wj/uUkplLvHMYKSXTwzchISFhBUgP34SEhIQVID18PbJOTy2gmXV8Dl8nRbj1+T8A5JTjNOtQW5EVNIkhnGqhtrxs20bTxYtMAReRG+bJ/ds0/e/RpuYroDlbStD6ea+bDHLabzHmycYW/m59vab2PAU09fOtL2/Cojme1THV5OrIBjdx/9uMf3uMsXvJfpHvv/C+VO5hvq+5SO5humtOkqtZQkJCwpEjab78o2uDKTHevUGJ2Spvzbyjs11+27p1eh2//R6t27X0pBt5mzN7qZp08fhCunylhlzRzBLd0nSmVc+lCwAZ6ga3phy88d+dzXw1ltuGJbf9/abAiCY2q7Hh2Lrz1LbTjivG+JtmJQdFbMy5MRk8cHj8avtH45/vC3ev8P3D95W712Kz0PB+dfewv68LajsD4mEEWSTZISEhIWEVSH6+HnmvH3yu3oprA1qH2ra/0/VvxU43o3ad5Q56vo/bXcuyuzmzlAgLdm3WjCg7PxzjiGm+h8CCQ3Y1m83GWF/zb83WcUNdebb2OY/+q0GrCKzVR+P+YcHr+naTPtwEjf23Oe7DYrwVCmVM8jil8evGdDjbq7NdwN8rsXvJ3Wtt7suxvYeDum3KfcPLl4YFma+IvBtlHbcNAA8DuN0Y84uRdW8G8HMA1gG8H8BPGWNmHszxr4+TkJCQcACIKVr9KXgjgG80xpwG8CIAPy0iL6xtX+QFAF6FspbbEwE8CcCtTfu1GuY7pfnmmjcDseBOr/SCCN6wPW77d4h7M/dy1qk0zZe0KXoFBZqvZVIx/axiHJyxX3OI51pWEQ+IzP6wxBh5g+brTgGzPp5uNeU0bQ7o0Nf1zBcz110G+9N02rBdP0dNLFnrawN3XL0Ig2zyjODrnCknh8cJjx/fFwn2UYIsJGgr1aZp/PN9oWq+ef1e26H7L7gvg/u1vIeLsb+vOVDEhRpPjhHzNcbcM9U1BvAVZdWXAHibMeZeABCR2wD8DoBXz9p+Yr4JCQknG8W43Z8CEXmriFwAcA+A1xtjPqWs9lQAd9HnTwO4QkQunbVbjQ9fEblMRO4QkW0RuV9EXtziO38qIoXIRVD2NyEh4UTjALIDjDEvB7AJ4PkAXi8i36GstgngHH0+b/+fUtat0EZ2eAuAPQCXA7gOwAdF5C5jzGe0lUXkx+x2o3O4bn9TjftmqaHbX/fttY79T2L/mt91nt6c6nftf798QMvX8vYGN5nYKRAX+6Q3ZDEuY9NDVx/fjkkMs8BT0EyVAvy6POXVMXtKvWi+hl5W7+9F3PUObnDT+vQS8ENb3JH3b1jo58DJDU2yRLjf9R3n446fg/J/EMCwoA7jxhSPs2D82TGZMZPj8WvHdJ75gKaYwc3dK4Pg/upQu9zGuR2fo4Hvy/HQ/+5k0rH76u9rxmR/t9xvkh6XhgMavo0xBsBHROT3ALwYwCemVtkGcJo+n7H/t2Ztd+bDV0Q2APwwgKcZY3YA3CkiHwBwIxQ9Q0TOAPh5AP8KwF/O2nZCQkLCkSCi5X/kP30SH/1Pn5xnS10Ajyj99wB4OkovBwC4FsBDxpjHZm2sifk+BcDYGPM56rsLwHMj678BwFsBPDTzR/ubYa7PygHb706X3qDubRqyXU9vNpnlWsGfXWLWyGDQt+0+G+EijMUxhiATPgdZaAY3hQUv6nIWGN8mdYbJ7GweFlxts8E1KsbkNCNTTwnh5mOIMT0tzDYWll1YmmuI7hZ0DhzznSh9Zb8o685mxk2Y5xzJgmy3cUxpJdrZyKawYGa+PP77yr3C94/mdsb332jf/xbfr9W1C0rPexbsngFH6Wr23O98Bp77nc+oPr/uV//Pqi0ij0fpZvaHKGf+zwfwL+3/abwTwDtE5D0AvgzgNQDe3rRbTZrsJrx+4bAFRcsQkW8H8CwAv9b0owkJCQlHhQU1XwPgJgAPomS7rwNwozHmr0TkKhHZEpErAcAY8yEAvwzgwwDuB/D3AH6hab+amO+0lgGUekagZVjD2lsB/GtjTEF5cNVXfW/jVJj3067Pbir81nRaL7Ph/sC/uQMdyq7Db+N10qxcm11mYvlKZWzf4sQcnKYGAHDtBlezNnDnQ8jVJ8vrrCqmvU4qFyJmcn55UxWGJvexXhCC6n/Ysbmcrp3mRhU7riYUdBCO7QV91M6txsh9PWKIzILd8YTMGGpb69M0+KZ8vnzcfD6kcdZSR9TVzNkheJzS+HUsuNPRxzzfF+5e4ftnU7nXtqlvd+jvy8mYzq1yX/Bxj4fl75pet7begbFADTdjzMOIzPCNMQ9gioAaY94M4M3z/EbTw/ezADoi8mSSHq4FcPfUeqcBPBPA++yD1F2tB0XkvzfG3MkrP/rJ91UP3MF/9TSsX/mt8+xzQkLCCcXuP96N3S9Ou9ceEMe0wO3Mh68x5oKI/D6A20TkZQCeAeD7UcoLvN5ZEXkCdV2F0iL4DJRheQG+9nt+PNQFXfUJonKa5rs28H38Bt7sd2v9GwrbBbx+FSQQIQbZYRJi9SdhHYraxmbdNyPPMgIrtGKZbkLAjjhhUKWt6t9rShQznzeDXd7R2WpGLDe35zbvMRuufy+oPDJHOsUg2MCy1JD5+uUTG2EyGfmbLSeLe4++NxmX64bMt86CY54V1fYbziH3a+elDZrGVDD+XCUIGqfa+O2s+S4e/3xfuHuF758NhQVv7vv7b4fO93hM++gClpQacIBPztP7Z9fhkn92XdX/2Cd/FwfFMsP8l4k2rmYvB/BbKCM7HgZwkzHmXhG5CqWV7xpjzIPGmCryQ0TWUWomDxlzTFMKJSQk/NPAxch8AcC6S/yQ0l/TPWjZ/fDSQ0JCQsLqcLE+fA8D/fVQVNfygnYVg9sp+t4l694Z+xIyvp2x62hGNm73ct3gUAVWAJCJYlDb3/NtxeA24SmgMt1hV5usYSoeuJq5PMVjfSLRlJ1LMwBphjPAG89YSsjpHIayQxZ8J7atLGJUmsvVzLmHDdnASbKA7Z+MKNCFHf1JjnASRR7Z1sheu3lyP0RlB3vtYq5mVUUI+k7okgXqd9IKG9ToGJzBjcapbHCQxcj+9+O8Q25nfF9oBjduu3ttl87hkMbnhI7BXbugzDy1O117XJHxfRBouTGOA1I+34SEhJONi1jzXTrWBl219DsHTjDzdcI+s90zCtsFyNVsjV3NOCuTBP+n20KMwrEDZglF4Go2rPUd1OAWy3bl23QsAUuosyot2IG3pRnOAM9488jyjBmxY8nK98vfzWrH0mR804xsZb8Lsqgb2QDPbJkZF8pyXkf7PuAZccytrWhiwYqxMjSmLs/gxuPP1UVjV7MsmM25MU0hwVRXTbsv+P7h+2rP7sMu3X/7EebrsN2h3MJk3R7b2UoRYfwHgTmMwI0lIDHfhISEk43EfD0Gm2HyDF93TQ9jdIyX2e7jaBuXEiPe7FnmS993fQCwpjDfDujijEgrsyzBDEnnHdY132JIQRgKS2mTYMcxIdZAg8AEezxC7KvJXSnYFuuwinsYs9yOnWnkirYLAB1y+dOYLzPqqj5fXmfD020H7RwClFSmmK3pMvMd745pOTPmcp3xHi0f+n2Z2ONhNmwiLm4atHMfBFZEro2Goon5DutBQLExK2uWBdI473R9Qiu+L9y9wvfPHjHbvXHZP1on3T3CXLUKGrt0vzut+FA032RwS0hISFgB0sPX48wU811TmC8HTjgdl7Xdyzb8Nk4R03LtU8x2SVtyyUICnXdMzGC873dMsRxXTuzULkbMrijlpDLdKRrcEnSdF3CeeyZnJhhbtwQzLY3lMltlNuuZb1brK9eldITdsj+j851168ub2G4MGgsOzjFp9I4B8vJx3y8PWa71dqCxE7DknmPRWe07gO7JUkRmJZ79z75esW0F/YV2Doj5VoE/NE7Z82FgvR1onHO71/Es2N0rHIjC95XTd8fMwjf0lJDOo4jv8e09f20c890/BOabZIeEhISEFSC5miUkJCSsAkl28Lj8dFg63mVS4inJOhvM7JQ3cC8jl5fTJFGcseuyM3ifi2m6AppkZAtlB2qPyuz6RczgZtuTYX3qW7brlS5i8EYZPYeCVIYWNpzVt8PfyRQjG+AlhpgRzUkMLC90+n46mXV53TX7ux11eW7748am9ga3KsBgqE+53bkf7/lpdKdPEsSen4qPd0d2/ziQhCQGa5zTpAjAywJs8NOuBxAzprZ3OwsNjHUjL48/NyZjBrfMjmnp+uQOPOa7lPTB3St8/4zpGN291hTgA3hDW2BUpzHpZIfhglkBZyHI8HaMkJhvQkLCyUZivh6Xn1oLPru3opYlH/CZlNjBm91fmAU749yg69nEoFN3nwkY7nDXt0eeNRW7F4L/QMgiHOsKDB5FnanNl9XMM4MgwAAuRJXXrQcu8Pe1YAgA6FbMts52y3bJcjsbg1ofAOTcttch6CODW3YIzDdgfWRwm1hm2xn2a30AkHO7u2v3n/oU41sQnELGNxe8UXQj10uhg6HBbUGjoxtTzIYV41vG45TGr9jaiELuZcH47/hzt2aNbxO6fzjcurCPj9jwzoLMgfV7nMOSXTvmqnYgpIdvQkJCwtHjYk4puXQ8/nTIfJ3mG+YS5WQe9byiZ/o6Cx5YTWlA2hLXoOoWNrxyuFP1aTov4LXeQD8jtx3HqjTdEWCH+GbnfMeETE6VGcDBCkWwXu37DSHBzHId881JK+9ueMbjdFxms7yc+zuD+rpZh4RB2+aafcgibQdmKkGVENsmDY9Da931GO/u1/oAILvgr51zgctJHw6X2yrAja5oeigz678uSDnZtykAACAASURBVCKLBFZo1zRk//XxU0R0b3e8+f5sO0VG4zzQf+m+6Nprs0YVhZnQO5Jq6F7kQ2Ep293bfF/vd/25Gw3KjR2G5ntcmW/7uU9CQkLCxYhi0u6PICI9EbldRO4XkfMi8jci8kJt8yLyUhGZ2Lpu7u/6pt1aCfO9bNAL3opOG5qH+W6wPswW1Ir50raEPBusvsVv/ow0r0Df3StZQKDzUttZmSdDPchikXpuMct3bpljjDFpqR1jmq5jsXl/rdbH7c46seGBX5f7pVe2ZY00RGK+VZvYU8CCGxD4aCpJY4QTyPR37f75azTeITZL7Nz1Zxf8eeH9mvT2bR95CtC5H+9ajZ2rSQcBMDTmJvVrunAlYyXQZKJ4PvA4FWa+dkwXPX8NMy5rkftzVOS2ggzZVAzdV4VR0qAKeb0I38+uErI/L/tj//2Rq1JyGIl1FvPz7QB4AMD1xpgHROT7APyuiHyrMeYLyvp3GmMaH7jTP5CQkJBwcrGAq5kxZgfArfT5gyLyeZSl0bSH79xv0yQ7JCQknGiYYtLqbxZE5AoAT0FZOq32EwCuE5Gvish9InKLiDRO71bCfL9mqpKFm550aSrW54ALpdx7n6Y/gXGtcgyn6fn+dtV2sgMbFgzJDm5aBngJwpAUwQYc1+Y+nuK4qeE8Wc0yfh8ql0/LTgb4YIFYDoZAVlgvJYKOIjWU7fryzLooAaHE4Pq5D4rsICQ7IHA7qx9kME1k1z1FdmBWY/ZtUAxdw27PX9u87/tzW6KcA0K4Pb6g5aSgqXzmAic4WELPDWwaohDmyWrmxlTO46xhTGY9P36d3CAkOxiWjMhSKJnN20GVLvtrvnKYUwh4ORcs4coe7n7ud/x+77Hs4IJWGvIkL4KDejuISBfAewC8wxjzWWWVjwF4mjHmCyLyLQDeB2AM4JdmbTfJDgkJCScaMdvLx++9Hx//z/fP/K6IZADeBWAPwCvU7RvzeWrfLSK3AXgljuPD99JBN3grasy3ozhoB7lGOVNZXm9nQ3IsJ5abDUsWLMSGiwvn1bbZK7cx2fXfZzcmF64azTBV5Z/VqyEEAQZ22hOt8+XyoXL4sBI40eQ+BgDd0+u15V0KqOhubpT7Mtjw+9r37Szot8yXmJRqfMvIaMM1w0Ux2lDBa26jKM+tUdgu4A2j/PtBgEGX3eHK/ljAhxb8EQSKZNZgR+uNcn/t2Tjn3NGajEn8m4F7WaG4mkUy6bkxmdM4zbrkVrlWXqdCM4oCyDiHtG0Xwb3KKQA2bB8dAy3Pxe+3v4cpVJmO61CZb+Th++ynXIVnP+Wq6vMv/cFHg+VSFpy7HcDjAXyvMWYey12jBpw034SEhBMNUxSt/hT8OoCrAfyAMWZfWwEARORFVhOGiFwN4BYAf9C0Xythvpf0O6CXKTK4LPe+L6gE21B3jZPkZJblSqDzEvvZtyHDF7aqvmLHtx3bBbzWy/oZuy5VQRaU2GQSBFnYt3mLzCNadV9mQlrdtS47t1vGG2OzrN/2Tq3Xl29u+t/aKHW9gO1unPb7RfpvxYLJXcmQblg4rZcYkcnaDzsp/PmEZcEyZj2TtGabl5bdqJiRM9sztt3NOJBFryJS9c0REqzZ12WOShgMrY4cj7OsqwSasItdj/IrOzsGnYuiy3o8zaxsW5TZCeCZW59ClXM6b93M7/dwYoL/QFgN2p2OAkfHfGdBRJ4I4CdRyg1fpqrLPwngTpSGt2uMMQ8CuAHA20VkE8BDKGWKNzT9RtJ8ExISTjQ461tbWF/eWW/bU7TuK1FqvHNhJQ/fzW54TC6xDrNhDrjoKJpvxpn4OVTSBVEM6x4OgNd0ix1d52VGPNouWcLogv/+eJcsy0pinVCLKyWiNm9ejVU1VZ/Q9N0mtgsAvdMlW803mO2errWzdW/ZFma+xDaNDU01lJCFmW/FcnMaag2aL0jnNaz5Tmyym64/x1yF14WJc9CAiQR/VGyPmF4nkvznoJjYccuhyFRQuBFBteZR3Tag6b88TrMu3R9VKH8s3DurtVnn5evh9NmMZic9YsEdClvuWBbco/D5EWvZtnkYiXVSboeEhISEFWAR2eEokB6+CQkJJxrp4UvY7IVTOidms5dVh91X7BxN9km7GdWz8wPerSzITsaywvbZ8v/WWXX5eNvLFU5uGF2oG9nKdil9cIWEIMuVNS6w29A8BTQlyN1gZQeSGjoDyi5mXcmapAbAyw2B1HDqEt9et7LDhpcdTM9/v2DZwU7xTZdlBzLgWAnCBK5m/hg1zyKWn4RWcMY3w1IDzd9l5DKoUR4J+t0smFLnrrO+AwS9HKSHlms3hrDA5uwxEayr9PM4k5zOgR0zfKwjxYWODYqdhnPAyDbIuF3lFibZbeLbORkC+24cULDNmHIDu8M1xzDI4rCQmG9CQsKJRpsI01VgJQ/fgUz5KjsRn0ImAxcj61qkGVcATFWisCGmgSsZMV/LeJntTi7U2W7ZtjXa2NWM8r86owbX8XK1vwByiG/jaqa4knFNMdef99i9jAwalcFNdzXLB+Qe5gxqzHY3L6ktN2vEdrv++yYwuJX9bGQbE1dzjvSTMTE9w4aW+rmRwKnf9+c2XL7ToRBqMq65KgwyoqACZr553Y2qiflyeHNXqyjBZdOL+rXndfPYQ8AFYcTKxXNgjstqRsuz3H8aZ/ZeiRgPRwrzncu4SMeYbUzcDvq+gl0taaaa18PMu3RtKgNgxK3tIODcx8cJifkmJCScaCTZgSC758LPjvkWEebrNN+xrvWZXc9yJ7v1IAoOnHCMl9nu8LxfPtyiUGLLfDU2DACTPZvPN0iiQm5Bw9k13ESpbBCr81VVXmC2yxUlbDtwNVunBDik31bMd1NnvoVlvIbZLrFgQ+5EI5u/lZ3nxzTY3USAQ0kD5os6ONyEc8J2qrzPptYHAL18zS5n1yk/xAtiVS5wIIsxraI+JjtcVUOpJ6eFlnObZ0hByLC75i2CMNywZ1mdx99B0ahxU808l+iIw80D5pv7WWIV1EE7HgTb2GtmDoH5JoNbQkJCwgqQHr6EbC/GfDmJCrFg+7o3kYqsnLXfuCAKSivIKSGdN8Nwy/cxmx1TW/d28G/+0Z4NslA8HIAFwxqJyWVBEh3LfLus+XKNNZsGkqtMcGDEOnk22OAJ9nYIdFzr2WDWfBBGQd4O+3RY+5baMvMdFnVHej4Vk0DzRQ0S6LyUQtOSIg7A6VF7XLg6Yf4crVEKxIDl2u1y0ABb8l2qShPYIfxyx4KLSBWTgBHba5fx8gUfCFUliyH3tfemadw+HWPP/laH+iRI51lP8ZlR7ThOzJTZMG8TeKLUgzsOg/kWSXZISEhIOHocV+bb6jUjIpeJyB0ism0Lyr04st5LROSTInJORP5BRN7UJqN7QkJCwmHBTCat/o4abZnvW1Bm97kcwHUAPigidxljPjO13gDAzwD4/+y6/x7AzwJ4E6+U7W2p5ZyDPK2jYa0/kBe40GVQINAa3FhqoAxPzrgWlRp26nkcNKmh3B+lfLiSuzcoeqlkLyvXsQYgxcgGAFm3NFjkipGN+zmLF1efCAxu1sWMDWdFz0sMTm5gqWGPprO75Da2N7ayAx13IEHYdfdpcI/mmBpzjuc16yrWowicES0fWdmBN88FH/t0PO4ss/EvYzcqd454nFI2NZdHOO/7Pr4emhyRd+tjB2DDq87Q1DEV9NXHVFMqGRNzi1PavG6HzkHlAsr3LWeUo/vSyQ5BlRPKplZVPGnY70XAhtDjhMaHr4hsAPhhlGUydgDcKSIfAHAjgFfzusaY36CPXxSR9wD450vc34SEhIS5cFxlhzbM9ykAxsaYz1HfXQCe2+K7zwFw93Tn5LGvhB1VmCKzjHq1goAZR1jwZN+G/CqGs7Jt3cd2mPkS2+WAit2R7ePS3PUMU6HBo36huS4bL+32ZpcUF4UFZxRkwdUpnFtZUGVioFefcAa1Yo3ZLocPl+2dsc52d8dc/rvs3yF3J247ZjwKqhbUM2Mx2L2sS+egm5Xb1er7cXsSZN6ic08/VVVhCNYl5usydg1onDGTs+3OuJ5LFwjHkbt2E8W1kMFuhqORXv2kGl90qxjarmPJecTw21HYbFOgSLCcGH3HMfqIkS0oWe+YbazWX9uglwVwMUe4bQI4P9W3BcpnqUFEfgJlmeWfWGzXEhISEg6OiznIYhvA6am+MygfwCpE5AdRZnJ/njHm0enlt/7a7ZWP0fXf9s24/tqrywWsqfEb2NXpYpax7x24mXE4lhswWIUFx1jK8IL/DafLsc7LLMRpvbHqtI7dFMR3c6VaL+BZT1C9gjVfy3g1nRfwtbmC6hN9ZsFUddbl4A3ChH3b6bsxtsvtrf2x/a8z333LOvbpO6M5mAgz3zXLeNeob4+3a8fMqeiwrlfZHdBxIwiNdQEEpJUTwzO2zewu7/sZFF8nN9b4empVSmJnpQh0WCVZE33TjblgnI4okZFLzKOEwU+3XYWWWL24jg21D8LY6b7M1/zMDArzDaqF2LDjj931n/GxT9+HZeJilh0+C6AjIk8m6eFaKHICAIjICwH8JsqCc1qNe7zmX/3gsX0bJSQkrA7XX3u1J2MAfvHdf3jgbcbI0SyISA9lDbfnAbgMwN8DeLUx5j9E1r8ZwM8BWAfwfgA/ZYyZmTK/8eFrjLkgIr8P4DYReRlKKeH7ATxL2YEbUNa3/xfGmE/Gtjl57Kthh9V6jRK+CXCtNK7SWq8izOuGzLeu6To9t+yj7e7yW945tHP4cF1/41DRIEhijvqk7nthwhMKsnCabyTIwnk5SETzNVzdwbI9Dh8eit+uY5MxtnuWztG2vSZbdI626To5xrtLbHhI29IqF+QcREH67sBqumvUN1LClgOiM9CHuKs1xh4lPQ6nrgIIKF2jomcKha7z9QhmLbbN1zOsFzfbxh9UMq7qAnLiHk68U2e+rC+7/jwY0xwST+HUSqUWZr4Te7x8r4Uh737MVUFCfU56xOfAab7L90xdUPPtAHgAwPXGmAdE5PsA/K6IfKstMVRBRF4A4FUonQu+BOAOALdiyiFhGm2fDi9H6Ub2FQDvBnCTMeZeEblKRLZE5Eq73i0oteA/sf1bIvLBlr+RkJCQsHRMRkWrP4YxZscYc6sx5gH7+YMAPo+SfE7jJQDeZoy51xhzFsBtAF7atF+t/HyNMY8B+CGl/wGEheRuaLO9hISEhKPCMjRfWxr+KSirFk/jqSjZrsOnAVwhIpfaZ6eKlYQXDx87G3z2eW912cHJDTy94anQWKsuwYUulSCJUF6gfKjc7wxqPLVtyN3AhhT3vQ4Vj2zSn2JBFi6PL5cBF6VEesZ9a34aXfQ4H2/ZLqj6xB650O2OnJHM7ytLDef2ffu8PbcsO5yn871r+3dp+f4csgNLDAOb62JAOS84YGPs8h5ETnE2oBLqYnPsctY0PncTm6eYctJy0dasZ0uwR8rU570datfzcmQNOXRj48SN1XnGIbuwuTGd0znkII7QlbKejY1L1k9sJRXOtDch2WHU9cZIJ0ewqyTLDi7X8jILlzosovkyRKSLUk59hzHms8oqmwA4YY3zDjsF4Hg9fBMSEhKOCrFkQ598+FH89SPRZyMAQMrco+9CGeH7ishq0x5hZ+z/qEcYsKKH7+4j59T+wM1FyRAVZI2ivKIay42xWcd82bCgGdl4f5gNNIFrc8GyizZvXseERKm3BXijTWBk4/BM68ITNbIp7f0gWILadn+3hnXDGhAyW8eCH73gr8E2GTC3bDs0uBGTajS4eYbmDG6n+n7YsvGu2Khno+VYBg5Vzm0u2S59nwqHYOBq00XOoTvPskOuU13dDdAb3CLXdg4W7B4ksUx6HvqYzW39RB7ngZGNDJQVyw6McHTt7DjgEOvJgI+bqpsoQUIx17tlIyY7PPPSS/DMS30e6//r7z4fLJeypMrtAB6P0nsrlgDiHgBPR+nlAJTeYA/NkhyAxHwTEhJOOArlBd8Svw7gagDPN8bsz1jvnQDeYdMpfBnAawC8vWnjK3n47p/dDj77MMbZmm+YL5UStSjJbkZ7de0W8CyX3/xhDbbZ1Yc1hKGi5E5UadntmXOMHVWJd5gtKHoj97Gmy9WFJ7biw5COmxPnXLBM/9yervNy2zHeR7aJ+dLybcuOdoYHdzVbtzOJ4URn7Bo4kVEQtmz1xqASBp2DXq88RxI5h5lyvoOkRgqri13bJhRKEEQRBFHorpAaXMAF68AFhWjzfeFqCPL9k9OY6NoZSMZ9NCsK6xHWma/mVnlcNF8ReSKAn0QpN3yZ6gr+JIA7UbLda4wxDxpjPiQivwzgwyi9wt4P4BeafiMx34SEhBMNfnm0hfXlnfUmCNIrGGPeDODN8/zGapjvY1tqhJtRwigB/2afBFbXeoIbXiem41ZpIEf6tgLduYH5anXXGK4/9JaI1XOrB1kEARXdevVX6dQ9H7hSQKztmCOzXfZscOHBrPNuK2wX8IyX+7aI/Tj9dxholJzIRUmsQ2x0l5jQrmVSzHaHDcyXq15w2yXh4SQ9e6TXuyoOecP5DJgvXw+6Tu7aBWw4YH318RMLovDhwXQ+Ff13njHL4z/n7bpERQobLr9X95zg+87py7xOTiw7lkRq2Tiot8NhITHfhISEE42LOatZQkJCwkULs7jB7VCxkofv3tld1f0jVghQy5sbShBsMCu3GwuicFO0YPtsAFLyy/KshWeIuXEfaAp5wGKGQfw/uyNZQ4WQ+06QIWqtXinA5NQmN6nhsF70krODOblhm87rY5QL49wOtW3/2R2SHWj50MoVY5Z+2D2sIZ9vRrLA2F7HccRg5wx1nYjBjjOkrduqEpwPeI2qXrhz0++RqxmdT5+li4Na2O3Mr1tdu7xuYJoXmqygjWUex8H4daeOSl0ERUqH7AI3tvvPhrO6cY6lCJYguO0kBv5+FsgOh1HDosRBi4oeFhLzTUhIONG4mFNKLh17j+0FnzVNphgWteWxHKSa8a2IGOdczld+GcZYgoaA+dp2j5gYv82dUbHNm1dzR2Ln+8pAQ4acoBKAbRdkFAK5RpE9De40MvPlHLwuVJj7OHDiLLHgR7ZL98dz5Go2pHUr5hsJCmgyuPH57Fgm1fR9dlXjUOTNNT/c3TFu9vx+DYjBuXPE563HbmdDGy7bqbNhu7NV0127rMGNMIYglNhVfeHxzwZIez7mG9M0e+CZhD2NXb4XezzLtAa3LrNd/bgcO86C2Vz9uJsCThZBMrglJCQkrAAsOx4nrMbV7HwYLOJ1LN3VrFpeRNgus1xF8+LKum6zYV/7NyPrY8qLGxntV9arH9c8CNzOnG7ILkrMtKweaTJK4kMaZVBReFIE/4GQ5bpQ4HPEcM+yzrtTDyUeUSWLffqe62fmO4m4UVXHRcw15/pk1TigXLV0PbY75b6sdfz+DYiVMQt2Wi8f96mJXz60eXGHVBm4yxq6O895ffZRHsPsazcPNPdHHv9B5WjbXs74tueA8mz36B7M7bXNOzHNl/T6iv3rOq+v3r187TdpvgkJCQkrQJIdCDHmy2iqlTZiFkxf1zQvjfnGNF8NgTVY6uvyy5qt99pFj1UYcMiyiC6oaL7syF8FAGjsDMCYquE6iZA9HLTqw6zzcpDFFvU7lru/V2e7vHw8qs9OgLB6SXVcVM2AWdVES52Yjaht94++s9nnUGff3hnUdW0+HxuWGY85wIGCJKqZRq5fD03zDfR8hQVrFSemUVWyMDqz1Zkv1HU18JB02+C+Hs9K7H3RY52Yzmd3tx5IonlAMA6D+SaDW0JCQsIKkGSHhISEhBUgyQ6E/XN6Uc/YVMpLBbOlBF6HU/A2basJmnsZtyfGd04C2cG5BbVwNVOmpqHsYLM+sZGNp67Wad9Q1YxCyCGeUpG6opNhDl+uZGGn5FwUk6tT0PTdSQyj/boUwf3joZeaJvu+oGmT7FBQ4IIp1pR1fdsZ53a79axqALBDlSzcMe5HMqSNKvnKb5/PZ+bOMwdLRIyh1bWLXtv2+XyrHNMRVzI//heTHQB2NbNSQSBF+HYvc7/FUkR9OQDk1nDJsgTLeRxYs2xogTzHAYn5JiQknGgMU3ixx4Wx7nfXFPgQe9vrBrXZb/42MxH3Fo8ZHBwLYCNcr6EM+DwIGJFSWpsrJxhHAcnIxueAS6w7I9JepJKFq7fGRjZmwWw8c8x2tFfvK/vLWmbMdidD3y4U5pvRMTIz9m1fj45d0XIbDttd898P2DvtlztGPm4+H+4cjSIuWx17ng1Rb74eQQl0x3wXdDXTEBv/bkzG7495xr8zuOkGZ8d4Y+N/WMxm0eF2m/dnUcwzyz1KJOabkJBwonFMJd8V1XCbOhtNyWzmY771Nzt/bx6nE7eN2FvZa76R31oosU69omv5wWnCdUZVti0TY+bL54XaruIv6517CvPdpXy+O4rOC/iEOUNilZq+O9rz1UuKsdf8uXpJtZyOUWPGrAkP6Xy58GPeP95vPh53jHsR3dudo9g5rM4zne9gVqJcuyySNGkeVEEWUftIXfPV7o8294HzTswUHbhs15lxNAmVMovU3TaXT4GPK/M9vAzGCQkJCccAE9PujyEirxCRT4rInoi8PbZtEXmpiExEZIv+rm+zX0l2SEhIONFYkPn+I4DXAXgByrpss3CnMabVA5exMtmhSWoI+2dLCdw/MvVpWZvf0KDJDeE+SKtttpEfmrI5VdPYiDuTN7ixexnUtosOHPE0myIGnZEqKHRJ67LBbVzlR6Z1ybjm5AbuY9mhGFNiWQvOFKbJEoErGuXbdfsSRNPRfvHxuGPk49bOx8To57M6z6JfDyjFIWNouvZN46dZoiPJaQ6DmwPfByPalpMIurR8oiwv23WJQv+N5UsEw3m0RrcXxtwBACLy7QCubFh9Ia0kyQ4JCQknGhNjWv1F0PRgNQCuE5Gvish9InKLiMx+21qsiPmGryLtLdzkalbMse7ibLfuHqOzb93gsFDJ6khuB83VjFlXZQCiPq5RGrCfSd2NaqgUpWQ3rDFnkVMYcWBkG9ZZbtjn2a4WZKG7l3kGydsaD/2McGLz9U4i+60V3hwqgRUAGdx4zAXMtzzPbOAMIj40V7M5AitiqApozjFLDO+VcL1Z29KgBhmJznY1Q10eWVfb/rJwQG+Hpm9/DMDTjDFfEJFvAfA+AGMAv9S04aT5JiQknGjEWO3nxjv4+8muuoww83VgjPk8te8WkdsAvBLH9eE7LEzj20hjuU2BE9w/j+YbY7YuHSlrRkxYNM23Sdw/aJy5RJgvLItgp3/Doc7MhJy7UYT5Vu5KnH0s4kLnWGYxGlIfabq2n9nupMHVLKaRum1NOvXtl9sd1PaP97vpGPl8uHPE5y04n+48M3tj/TdrNfOMommcxO+F+nLN1SwW9TXP/aG7j+ltfw/ryw8TsVP5jfk6vjH3ATv/z+hRbbVFbthWR5Y034SEhBONRTRfEclFpI+SoOYisqZpuSLyIhG5wravBnALgD9os18rY74MzRjZpEnNEz7c7Gqiv6i0IAtNaw6371eu2FOxgLkVEc238Uuk+dLeFsr5GEUCCDQ9dBJjiFbzDQInSKetNF+FDU+vWx1CoR9rNu5Gtx/sCx+XovNyOwg+0YIRItppMOtogqL5zgMeP1qSGM2zITbitHzWsW1NfweY1mnrNo+QKNYTTsXuJYfDYIMLTjZfA+Dn6fOPA3itiLwDwD0ArjHGPAjgBgBvF5FNAA8BeBeAN7T5gaT5JiQknGiMGslXHcaY1wJ4bWTxKVrvlSg13rmRHr4JCQknGsc1vLjx4SsilwG4HcB/A+BhAK82xrw3su7NAH4OZdqp9wP4KWNMLXnv9HSjObdDeylhMVca3f1FzwB1RFaCGMjiZwKDW33CFhqLfFuztWg5DLhQJbcLRYIIpIBAVnA5jXX3MU12CI4h+F7duBf8rt2XIihTpB+DO8ZJxPDkumPnsIJErscSM5gdFLGAC31509Y0WUH/vm58i0kUbvFh5HZY+iaXgjYj5C0A9gBcDuDHAPy6iDx1eiUReQGAV6HUQJ4I4EkAbl3eriYkJCTMjwMGWRwaZj58RWQDwA8DeI0xZscYcyeADwC4UVn9JQDeZoy51xhzFsBtAF6qbbd+4FD+2p8U/Xu+b7Hvx5h1ffnfjXeaf+SIYESqvxgmhSn/+BoU/s/hsb/7m6pdGFP9Bb9XTGp/TcsP+jfP70/vNx9TcC4i56PpPB8XTI/Becbxwe+Veb7f/r5f1gNxkcQ6R4Em5vsUAGNjzOeo7y4AT1PWfapd5vBpAFeIyKUH28Xjj+P08F0mHvvc3zSvdJHhJB4TcHLH4DJwXJlvk+a7CeD8VN8WyNo3te45+uy+dwrAYwvtnUVT4MRxwnHSlxatnjJxOq0J3bbaoknHPSgW3X5RmOqYJgu4/x2najTHaZzFoLlgHlVgRbgfR/+bbdD08N0GcHqq7wzKB3DTumfsf23dhISEhCPBca3hJmYGm7Sa76MoE0d8zva9C8A/GGP+t6l13wPg88aYW+zn5wF4tzHmCVPrHc8zkZCQcCxhjFmYL8/7vDnIb82LmQ9fABCR96L0CXkZgGcA+CMAzzLG3Du13gsAvAOlt8OXAdwB4C+mH9IJCQkJCe1czV6OMpP7VwC8G8BNxph7ReQqWzLjSgAwxnwIwC8D+DCA+wH8PYBfOJS9TkhISLjI0ch8ExISEhKWj6WH4YjIZSJyh4hsi8j9IvLiGeveLCJfEpFzInK7iPSWvT/LQtvjEpGX2MJ750TkH0TkTW0z2x815rlW9J0/FZFCZJ7MMkeLOcfgk0Tkj0TkvK1G8Kaj3Ne2mPOYXmPH3lkR+bAWFHUc0LZIpV33onlWtMVh3EAnNSKu1XGhlGh+BsDjAHwngOcB+Nmj2sk50faYAAAi8mMoPWSO+3Sp7RjsIZdfSAAAA1ZJREFUAfiPAP5fAFcA+DqU0tpxRNtj+gEANwH4HgCXAfhLlJm2jiNckcrfmrXSRfisaAdjzNL+AGwA2AfwZOr7bQBvVNb9HQCvp8//HMCXlrk/qzgu5bs3A/j3qz6Ggx4TStfB+1C+UAoA2aqP4aDHBeAnAXx01fu85GN6NYD30eenAdhd9TE0HN/rALx9xvKL5lkxz9+yme9JjYib57im8RwAdx/KXh0M8x7TGwC8FWXO0uOMeY7ruwB8QUT+2EoOH7Z1uI4b5jmmPwXwLBH5JhHpogz7/5Mj2MeDoMm962J6VrTGsh++y4qIO26Y57gqiMhPoHTP+5VD2q+DoPUx2fLZzwLwa0ewXwfFPNfqSgA/CuBXATwBwAcBfMA+tI4TWh+TMeYTKFnxfQB2APwIgP/lsHfwgGiSsS6mZ0VrLPvhe1Ij4uY5LgCAiPwgSrb4ImOMWhxqxWh1TNaw9lYA/9oYwzG5xyerTIh5rtUOgI8bYz5kjBkbY34FpVZ/9SHv47xofUwi8gqUdoYrAayhTHD1ZyIymF73GKFpLF1Mz4rWWPbD97MAOiLyZOq7Fvq0+x4AT59a7yFjzIHyQBwS5jkuiMgLAfwmgP/OGHPPEezfImh7TKcBPBPA+0TkSwA+YfsfFJHvPvzdnBvzXKtP8weRY5SmLMQ8x/RCAO81xnzRGFMYY34bwKUArjmC/VwUTcz3YnpWtMchiOfvRSmQrwN4NoCzKOsdTa/3AgBfQjkoLgXwEQBvWLUIvoTjugHAIwCevep9XuIxXU5/347S4PYEAN1VH8MBj+spAC6gZIo5SuPo3wHorPoYDnBMbwDwcXutMpTpX7cAnF71MSj7mgPoA3gjgHeiZOq5st5F9axoffyHcEIvRRlavI0y0u1Hbf9VdhBcSevejDIU+RzKahnH8mae57gA/BmAoe1zfx9c9f4f9FrRd74BwATH1NthgTH4Q/aBe85eu9oD7Tj8zTH+1gG8je6rTwL4b1e9/5Fjei3KFzn//fzF/qxo+5ci3BISEhJWgGMbpZSQkJBwkpEevgkJCQkrQHr4JiQkJKwA6eGbkJCQsAKkh29CQkLCCpAevgkJCQkrQHr4JiQkJKwA6eGbkJCQsAKkh29CQkLCCvD/A0jSkWfiU/75AAAAAElFTkSuQmCC" alt="" />
aaarticlea/png;base64,iVBORw0KGgoAAAANSUhEUgAAAXoAAAEECAYAAAAmiP8hAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAIABJREFUeJzsvXeYHWd59/+ZOb3v2aZt6r3LkizLkmXLBRuwAYNtnNiAKcEvgSTkzQskkJdgQl4gjQDJLyEkEFpMi02oLrjIkmwVy+pWrytt3z29TX1+f4xWlhXJmjnn7GpXOp/r2sve1TzPmXPOzHfu537uIgkhqFGjRo0aVy7y5T6BGjVq1KgxstSEvkaNGjWucGpCX6NGjRpXODWhr1GjRo0rnJrQ16hRo8YVTk3oa9SoUeMKpyb0NWrUqHGFc0mhlyTpDyRJ2iZJUkmSpP+4xLH/W5KkHkmS0pIkfUuSJG/1TrVGjRo1apSDHYu+C/gC8O03OkiSpDuAPwVuASYD04DPV3qCNWrUqFGjMi4p9EKInwkhfg4MXeLQh4B/F0LsF0KkgL8E3l/5KdaoUaNGjUpw4qOXLvHv84Bd5/y+G5ggSVLc8VnVqFGjRo2q4UToL1UUJwykz/k9c+a/EUdnVKNGjRo1qko1LfocED3n99iZ/2YdnVGNGjVq1KgqbgfHXsqifxVYAvzXmd8XA31CiOS5B0mSVCuXWaNGjRplIIS4lMF9QeyEV7okSfJjPRRckiT5JElyXeDQ7wEfkiRp7hm//GeBC4ZjCiFqP0Lwuc99ztZx62+5k0JXd1mvkV33OIUdL9g+3hjsxEj32zq2L1MgU1RtHbvu6ACbTyYcfRYP//sWNh8ZuOzfU7V/iqrOtZ99wtFncSpZ4AfbT9maX9UNOoeyto41S3n00/ttn7va20ni0a+U/d7X3/xWit09to+3e49cDT+VYMd181mggBU6+R6gCPy5JEmTJEnKSpLUcUa8nwL+BngeOAEcBT5X0dnVAEAYBpLrQs9WG0gymA4uEkkGmxeVLEm2L0CvS0bRTfvnAdSFvCRyqqMx44FETqE+7HM0RjFMfG57nlYhBJJk0/ATwvrO7WKaSHL5eZaSLCNMZ9dBjcq5pOtGCPEI8MhF/vl1G61CiH8A/qHis6rxOoRhILudeNleQ3K5EKbuYIAMwt6NKEv2nyEBj4uMotg/D6Al5qc3XXQ0ZjzQmy7REvM7GlPUDAJuew97Uwhkuwt8YYIT4TZ1KNfoACS3G6EbZY+vUR61EgiXkbVr19o6TmgaUplCj8sNhkOht2lxyZKEadOiD3ld5JWLn8eFPouJDUFODORtzT+eODGQZ2JD6KL/fqHPIq8ahLz2BNYwre/GFsJ0ZNELQ0eSKxB6jxtT02wfb/ceqfHG1IT+MmL3IjZVDdlXXjUJyeVB6A6E3uUC057F5ZJlDJsPhajfQ9qh0M9pjXKgO/M/Dx7nHOjOMKf14lHHF/os0iWNmN9ja35DmLhsWulOhVvoOrjtnceFkL3emtBfBmpCP8YRQmCqKrK3TKH3eBC6/RtLkt22XT0uWUK36bup83tIFzVHm0ozWiKcShTecCUwHtl7OsW89tilDzyHZFGjLmBvVWcYArdd341pgBMLXVeRKhB6l8+HWSqVPb5GedSEfoxjFkvIfl/ZG2CSx4fQHNxYDlw9bllGN+xZ9D63TMDjIlWyL9p+j4sFHTFeOZ6wPWask8yrnBoqsKCjztG4wbxKY8jeBq5umrhdNq8XQweXfeEWqoLkdbaRfC6uYACjWBP60aYm9GMcPZ/HFQiUPV7yeBGqg01QlwcMeysAj0vCMO2HfjWFvAzknG3IrpzRyIuHBhyNGctsPjLI0qn1eGxG0ADkVB1TCMI2ffSaE4ve0KyHu02EpiB5nG0kn4srGMTIX3n7LmOdmtCPcfRsDk+k/CoSki+AUBxErrg8oNtzsUiShEuW0Gxa9a1RP90ZZ9bcbQtaeGZvr+2Vw1jnyd093LagxdGY7kyJ1qjfVsikEALNMPDaDcXUVSS3fbegqRSRfOULvTsSRsvmyh5fozxqQj/G0bNZ3JFw2eMlX9CR0EuybPlsbbpvvG6XbaFvj/o57TBcclJDiLZ4gE2HBx2NG4skcgrbTyS4eW6zo3Fd6RLtUXviapgCkGxvxmJo4EDohVJE9gVtH38+nmgUPXPlbbCPdWpCP8ZRkyk8cWf+3HORAyHMosOlsscLuj0Xi9dtPxGqLeZnqKBR1JzFUd+/cjLf2XDM0ZixyH++dII7FrYSthk9M8zxRIEpcXviquhOEqtM0B0KfTGPFLh4aOilcMeiaKn0pQ+sUVVqQj/G0ZJJvPHyKz1LZQi95PEjNHtC73O7UGwmwLhlmUl1AY4lCo7O582LWulLl8b1pmymqPHY1lN88KZpjsalitaDsSVibwNU0Q18NhOr0FRwe+1n0QJmMYdcgdB76+OoieSlD6xRVWpCP8ZRBxN4GyoQeo8PEM42ZD0+UO25WIaF3u6G7MzGEIcGnPlo3S6Zh2+ZwdeeOoDppJzDGOLfnj/CrfNbaLNpmQ9zcCDHjMaQbTFWNAOfx67Ql6zv2gGW0JfvSvQ21KMOjd8H9nilJvRjHGVgEF9zU9njJUlCDkYxC/b9opInYDsk0yVLeGTZtlU/szFMZ6ro2H1z15J2DBOe2N3taNxY4PhAjl/t6OJjb5rpeOy+/izzmu1txptCoOgGfpsWvVCLSF5nEV1mLoMcdpYDcC6+piaUgfG/3zLeqAn9GKfU11eR0API4RhG1oFf1BsAtWjbSg94XRRVe8Ltc8tMqw+yv99ZmwJZlvjUXXP56pMHSRXGT6Ez0xR88eev8qG10x0XMuvNllB1kw6bdXFKmhVtI9sMrXQq9ELXEWqpIh+9v6UZpbev7PE1yqMm9GOcUncv/va2iuZwReowc/b9opLbY9U/sbkhG/C6Kaj2E6GWtMXY0Z12XHp18aQ4dyxq5Qv/vbfisq2jxQ9eOoGim/zu9VMcj93RnWZJW8y226ao6gS99mLihRCg5MFBBI2ZSyGHY0hOql2eh7exAT2bw6hlx44qNaEfwwghKJ7uJlCh0MuROGbGmV9U8oUQir1NU7/bhW4K22GWHTE/siRxIum8MuUf3T6LvlSJb6076njsaLP5yCDfXX+ML9+/GJftcpIWBdXg8GCehS3RSx+Mda3kHQg9ugqS7CiG3sgmcEUqawEtyTL+1haKp8efC248UxP6MYyWTAFUFF4J4Io1YKQdboD5w1Cyt2kqSRIhr5u8Yi+jVpIkVkyMs6XT+aac1+3iK+9ZyuPbTvOL7acdjx8tDnSn+cxPdvG3D1zjeAMWYNvpFHObwwRtZsMquoEsSXhslj4QpRyS39mmqpEaQo41OBpzIYJTJlE42VnxPDXsUxP6MUz++AlCUyc7Cn+7EK66JoyUszICkj+MKGZtu0hCfjc5Rbd9/NzmMFnF4GTSWaglQHPUzz89tJyvP3WQDQf6HY8faTqH8vzR917hz98xn6VT6h2PL6gGu3rSrJho33rOKTphn9v+tVLKWQ9zB5jpQVx1jY7GXIjglEnkjx2veJ4a9qkJ/Rgmd/Aw4ZnTK57HFbeE3pFfezjszqaf3u92Wa3mbCZPyZLEjdMaeP7ooO2a9ucyrTnMP7xnGY88vodf7uhyPH6k2HsqxYf/fQsfuXUmt853VupgmA0nhpg/IWK7LLEpBHlFI+yzd7wQAlHMIAWcldbQE/244s6yei9EeOYMcofGvuvtSuKyCL2p2bf8rmayBw4RnjOr4nmkM3HPomg/fl2SJKRAFGEzLFOSJCJ+D5mS/YiYWY0h/G4Xu8qsOb9wYh3f/L0VfPO5w3ztqYNn0v8vH0/s6uYPv7eNT799Pu+6dmJZc/RmSxwZzLPKwUogr2j4PW77FSuVArg8jvzzAEayrypCH5k7m9yBQxXPczUgDAOjVMJUK4s0K7NtUWU8v+wGqz2e34c7EsEdCeOJRvA2NuJrbsLX3EigrY3g5IkEJk3EEy2/qNd4JrPnVdrvfWfF80iShKt+AvpQL96g/c9SCkYx0/0Qs3dzR/weTifzGKa9xheSJHHrzEZ+vKuLGY0hIj7nl+P05gjf+8gq/uxHO/n9/9jKX927mGaHbfoqpagafPXJA7x0eIBvfHAFs1vtbaCej2EKnjo0wI3TGuzHwgtBuqhRb7OEMYAoppGCzs5RaCpmPoMrVrnrJjR9GqXePvRsrqI6TuMVo1iiePo0hc7TFE91ofT3o/QPogwMoKUz6NksejaPUSiAJCG73Uz58Psres3LIvS37t6MME3MkoKey6FlsujpDMrgkPWm+wbo37+OYucpCidPIft9RGbNIDRzBpHZM4gumEdo2tTyG2aPA7R0hmJXD5G5s6syn7uxDWOwByY6SNoJRGCwE6FrtppNuGSZkM/jSHiaQj6Wttfx1KF+7lnQWtZ+RDzk5Z8/cC3fWneU+/9pI++/cRoPXD/FUSngchBC8Ny+Pv7uN/tZOrmeRz+2mojDOjbnsvVUkqDHxYIJ9h/GRc1AwurJawchBCKfQm6a4ujc9KFeXHVNVbnnZI+b6IJ5pHbuonHN6ornG6sIISh195DZu4/sgcPkDh0md+gI6uAQ/o42gpMmEuhoxzehmei8uXibGvHG63CHw7ijYVyBwOs/7489XPa5XBahByvMyhUM4AoG3jAhSAiB0j9A7tARcoeOkNi0lePf/A7q4BCRObOILpxH3dIl1F2zGG+D842vsUrqlR3EFs1H9lTnK3I3tqF1O9sAkyT5jPsmhRS1l7QVC3jpThWIBby2QwqvmxjnBztOs7M7wzUOOy8N45IlHr5lBncsauVvf72fx14+xUdvs/zkdiNR7CKEYMfJJP/yzGESeZW/vGcR106rLBqlJ1Pila4U71s60fbDTghBqqAQCzqoVzNc2sJhRqw+0IW7qbIw33OpW7aE5JZXriih1/MF0rv3kN6xm/SuPWRe3Y/kchFdOJ/I3Nm03X0X4VkzCHS0j7qRKo22r1ySJFGN19QyWbL79pPetZfUjl2kd+7G21BP/Lprqb/uWuLXLcNbV1lY4uVk/yNfJDh1CpMfeqAq8+kD3WSf/AHx937K0ThRzGImu3G12V9ZDGZLyLLkyJ2QLKg8urOLd8xvoSNWfqOVYTYfGeTfnj9C51CBu5d18K5rJ9JaV9m82ZLGb3Z2819bO9ENwXtvmMrbl7bb941fhLyq8/3tp7l1RiMzG+27MvKKTrKg0F4XtC305tBpcLmR65xtFGef+THu5g4Ci6ojzOnde9n32S9w/c9/XJX5LgdGqURq+y4Sm7eS3PwyuWPHicyZTd3SxcSWLCK2YF7FWe3nIkkSQoiyQvAum0VfKZ5ohPqVK6hfuQKwNi1yh46Q2LKN7p/9gn2f/QKhKZOoX72S+uuvo27JImRv+cvq0USYJoMvbGTp+x+s2pyuhgmYuRSmUkT2ORA8fxgMHaEUkGxmUdYFvXSl8kT9HtsiGA96ecvsZn65r5cHrumwHXFyMVbOaGTljEaO9md5bOspfvefXqQtHuDaaQ0sn1rP/I4Y8dAbW8LZksaR3izbjifYdjzBq6dTrJ7VxKfumsfyqfUVh70CaIbJz1/tZUFLxJHICyFIFhTqgz77KwDTROSTyK3ON/j1vk4Ci1Y5HncxogvmoSVTFE6dJjixo2rzjiTCNMkdPMzQpq0kXtpMetdewrNmUL/yWmZ+8uNEFy3A5Su/zeJIMm4t+kthqhqpnbtJbNpC4sXN5E92Ur/yWhpvWkPjmlX4mirfVBopElu2ceivv8LKxx+t6rzpx/+FwDU34Z06z9E4M9ULuorcOMn2mGRBQdVNJkSdWdHbu1Ls6E7zwJIO235nO2i6yZ7TKbYdS7Dt+BCHe7OUNJPWOj/NUf/r3ExDOYXuZBHdFExpDLH8zMPhminxinzw52MKwS/29eKWJe6cM8HRgyNdVCmoOi3RgH1rPjuEKKRxTXBWKtks5kl+94vUP/yXSE4aiV+CA3/5ZbzNTUz7yIeqNme10fN5Epu2Mrj+RQZf2IgrEKBh9UrLgFyxDHd49DaTK7Hor1ihPx91KMHgxk0Mrd/I0EtbCE6aSOPaNTSuXUNkzqyqWGfVYsdHPk7T2jV0/M69VZ23sOVphFoitObtjsYJQ8fs2o/cPhfJZn9RUwi6knkawn77aflneOHYIKdSRe5b1Ga/tnoZ5BWdnlSR/kwJ85zw//qwl7Z4gFjAM2LXhRCCpw8PkCpq3LOwzX6PV0A3TLpSBVpjQfstA4XA7D6IXN+GFHAWcaMc3UNpzyZid5e/GXghsvsPsuP3/5jVT/wMV2B0I6XeiGJ3D4PPb2Bg3QbSu/YQW7yAxhtX03jjDQQnlxc2Ww1qQu8QU9NJvbKDwRc2MrBuA6aq0LT2RppuuYn4tUuRvc7ii6vJ4AsbOfjlr7Dyv39Y9WWg1nOc3HOPEX/wE47HmoOnLN9uvNX2mIKqM5Qr0V4Xsl1RESxRevbIIF2ZEvcubCXk8EEx1jFMwRMH+8gqOu9a0Ga7IxRYn01fpojP7SLuJKSykMFMdiO3zXb88Mo991/IdQ0El97saJwd9nziMwQmdjDj4x+t+tx2EaZJdt8BBp57gYHnN6AMDtK4ZhWNN62h4YaVuEPlV+usJjWhrwAhBIVjJxh4fj0Dz79A/uhx6letpOmWG2m8YRWeuvJrbzvFKJbYfPf9zPncZ2hYdV3V5xemSeLfP0fd7/4fXBFnG9VCUzB7Djmy6gEGslaVwqaIM4tNCMFLJxPs789x36K2in32YwXVMPnlvl4k4G3znEcEZUsamaJKm4MNWCEEZu8RpEgjcthZUTIhBMnv/D+ib/893A3lZfq+EUr/AJvf9QDLv/tNQtOnVn3+i2EoCsmt2xh4bj2D6zbgCgVpuvkmmm6+kdjiBWMydLsm9FVEGRxicP2LDDz3AsmtrxCZO4vGm9bQdNMNBKdNGdGl/N5P/jmy18v8Lz4yIq8BkH3qP3G3TCaw+AbHY83BTnB5HFn1pinoSuWJB32Oe6WC5bPf3JnkbXNbmFhh1MzlJl3S+PmrvTSGvNwxq9lxRUtVN+hJF2mNBfA6cGlZ1nwXctscx9evPtBF5tffIf7QZ0bs2u/66c/o/P4PufbRb4+oz1vpH7B87etfJLHlZSKzZloG3do1hKZOGbHXrRY1oR8hjGKJ5NZtlovnhY1ILhcNN1xP4w3XE7/uWtwh51UJL4QwTY5+7Z9JbH2FZd/5xoju3CtH91LcuZ66e5wvlYWuWn7etjm2EqiGKVeghjmeyPObA/0sbY+xclJ8TO2n2OXwYI6nDw2wYmIdyzvqHL8H0xR0p/PEAj5HG8JnffN1LUgh5+HG+Zd+A8IktPoux2OdcOALf03x1GkWffVvcAWr80A3NZ307j0MbXiJoY2bKHb10LD6OhpvuoGGG1bhrbAq7GhTE/pRQAhB/shRhjZuYmjjJiu0avZM4iuWEV++lNjiBWVZI4nNL3PkK/+I5PGw6Kt/PeLRQELXSHzr89Q98AnH7hsAM9EFpuEoAgcsl0OqoNBWF3JsyQJkFZ1f7e9FQuItc5rHjStHNUzWHR3kRLLAXXNbaIs633QUQtCfLeGSJRrDzsab2SFELoHcMsPxw0UIQfK7XyL61vfibh7ZTUhT09n/+S+S2LSVaR97mLZ33OnYfWKqKtkDh0i+vJ3ky6+Q2rGL4MQOGtasovGGVUQXLahaAuLloCb0lwGjWCK9azfJra+QfHk7mf0H8Le2EF0wj8ic2QQnthOY1EGgvR3Z/1qss5bJkjt0mOzBwwyu20DxVBfTP/77TLjjNiQb9WGqQfbZn+KKNRBcfovjscI0MLsOIDdNdlzPPJEvUdJMWmIB5DKsclMIXj6VYuupJNd21LF8YtxRtMpoIoTg4ECOdceGmFwX4JYZjWVFEAkhSOQVVMN0FEoJw9FSB5AnTLOdA3EuWtcxcs8/Rt2Dnxi1VVRq526OfOWf0FIpWt/2VsJzZhKZPQtvU+PZczB1nVJPL8VTXRRPnSZ38DCZvfvIHT1GcNIk4tcuJX7tUuqWLx13VvsbURP6MYCp6eSPHrMuuENHKJw6TfHUaUpdPZiqiuR2I7ldSJJMaOZ0InNmEVu8kJa33jHqiVxa93Fyz/6Euvd8qqwb2MwnEak+5LZZjtrKCSEYyJYQQHPEX7Z4pIoazx8dZDCvcuO0BmY1hsaUO6cnU+KFY4OUdJPbZjTRUcHeQqqgkFN0WmNBxyshc7ATJBm5obyEpOwzP8IVbya4zLlBUAlCCIY2biKxaQvZA4fIHTyMUSxZCV+6DpKEv2UCgYntBCd2EJo+leiC+UTmzKqa22csMu6EPv2r/wCXC8ntRfYFkPxBJF8QORzFFa6z+lIGwmPq5q2E4QvU1HRcft9l39EXQpB69O8I3fgOvBOdZ0kKITD7jyN5/chxZ/VPht0QUJnYA5xIFHjh+BCmKbh2Yh1zmyNluYWqgRCCk8kiW08lGSqorJpcz8LWaFkrl2GGRb4lFsDtcLUnCmnMRJcVTllGkpNZzJP83peIv/dPkR1UPB0JhBAYhSKS24Xsdl/2+6eamEoRM5fGzKaszPVSAaEUMEtF0BSEaYBh4J2xiMC8a8eX0JcO7bTegKZiKkWEUkSU8hi5tPWmcykwDFzxJlzxZlz1E3A3teNuakcOlVcCtsbrKe7ZhHZiP9G3fbCs8cLQrE2+pimOXTjDseCSJFUs9ucKbKKosaglytzmMPHg6ORCFFSDg4M5dvdkMEzBiio8cKzSwyrZkkZrLOi4lk4l380whVeewxjqI3L775Y1vsbrMZUixkA3+kAXeqIXI9mPkRxA6OoZ49YycOVACMkXRPIHkDw+K5RZduGKN+FpaBlfQm/nNc1SASM5gJHsw0j0WR/QQBfILjytU/C0TsXdPhV3U3tV07KvFoSmkvjuF4nd/b9wN9oPl3zdHIU05tBpy4XjcuZ+GrbsTVPQHA1UxRLvyyrs7ctwoD9H1O9mdlOYyfEgzZeoaeOUVFGjM1Xg0GCernSJ6Q1B5jVHmFpvP7b9YgghGMorlDSDlmjAucgLgdl3FMkXchQG+7o5dI3kd79I9O0frmrFyqsFIQRGagC96xhaz3G07hOYhQzuhlbcTe24GlotAzbehByK2r5mRtR1I0lSPfAt4E3AIPBpIcQPL3LsZ4GHgQiwA/iYEGLfeceU7aMXQmBmk2g9J9C7j6N1H8PMpfF0zMAzaTbeybNxRa+cUsUjTWH78+i9nUTf+lDZc5jJboRSQJ4wvayojkReoagZTIgGqlZO2BSCzmSRw0M5TiaLlDSDjroALWEfjSEfDSEPMb/nkm4VIQR51WAwrzJYUBnIKZxKWzVwJtUFmFYfYkZjCG8Vz7s/U0QAEyIBR9nEZ+dI9iCUfFnfxzDFHevRuo8RvfP9ZY2/GjFLBbTOQ6idB9FOHgRJwtM+DXfbVDxtU3HFJ1QcbDHSQj8s6h8CrgF+Day6gIC/HfgXYDXQCfwVcIcQYtl5x1V1M9bMZ1A7D6F1HkQ9eRA5Uodv2gK80xfiami5Yvz8I4HQFJLf+zKROz+Ap8VZuOTZOYYtSI+/7E2/TFElVVBpjDivi2OHrKJzKlWkP6cwmFcZKqjkVB2fSybgdeF3uxjWVCFAMUyKmkFRM/C7XTQEPTSGfDSGvHTEAjQEq18DRzPMs6UNGsP2K1Kei5lPIhLdZa2wzs6hFEl+/6+J3f0w7saaNf9GGLk06tE9qMf2ovd24m6fhnfybLyT5iDXNVb9GhkxoZckKQQkgPlCiCNn/vZdoFsI8enzjv00sEQIcf+Z3+cD24QQgfOOG7GoG2Ea6D0nUI7uRT26B8njxTd7Kb7ZS2uW/kUo7dtKae9mYvf9YdkXpjB0zN7DVoq9zQYl51PUdAayJcI+N3EHpXfLxRSCkmZS0HRKmsm5V6TXLRPyuAh4XCO+uSuEIKfoJPIK8aCXiL+8h4go5TD7TyC3TEdy2FTkXPIbfoGpFIncdn/Zc1zJmKUC6pHdlA68gpHoxTtlLt7pC/FOmo3kGdl9oZEU+muAjUKI0Dl/+xNgrRDi7ecduwL4L+BW4ATw/4AZQoh3nXfcqIRXCiHQe0+gHNiOcngnroZW/AtW4pu+0FFW55WOECapH32NwJI1+OcuL38eTbHqqcTbHNdTGcYwTQayJQxT0BTxl5VFO54wTJPBnIJmmDRX8H6FWsTsPYrcNMlxZcpz0Yd6ST/2z8Qf/EQt6OEchDDRTh+htHcz2smDeCbNwjd7Gd7Jc5Dco5eANZKNR8JA5ry/ZbF88K9DCLH1jLV/EDCw3De3lnNS1UCSJDytU/G0TiW05h2ox1+ltHcz+Rf+G9+cZQQWrcZVN3Zr0o8WkiQTufVe0r/4Ft7Jc5CD5UVpSB4f8oRpmL1HEZJUVrq9S5aZEA2QUzR60kUifg91QW9FIYpjkXOt+LDfTVMkWPZ7FGoJs+8ockNHRSIvhEnuuZ8SXPnmmsifwSwVKL26hdLezUhuD/4FKwnffC+yvzqlT0aTSwl9Djj/W49hif3rkCTpD7CEvQPoBd4LPCdJ0nwhRPHcYx955JGz/7927VrWrl3r9LwdIbnd+GYuxjdzMUZqkNKrm0n95Ot4WqcQuOYm3O3Trmpfvrt5Iv45y8ite4zIW95X9mcheQOW2PcdQ0Igh5xb9pIkEfF7CXjcJPIKXck89SEfQa/7iviOFM1gKG/lEbTEAhXV2xdq0fqs421lPVjPpbRzIwD+hSsrmudKwEgOUNz5AsqhnXinzidyxwO4J0wa9etv3bp1rFu3ripzleOj/z5wSgjxmfOO/RXwlBDiH8/5WxK4VQix/Zy/jYnMWKGplA5so7RjPZIvQHDFm/BMmXtFiEk5CF0j9ZOv419wfcUt484KUGwCcrSyVVNRtSxfJIgHfQQ8rnH5HSm6QaqgouiGVcnTV9mDa9gnLzW0l/VAPRetr5PML75F3bv/CFessibn4xl9oIvCy8+gdR3Dv/B6AgtXjanVzWhE3Qjg94ClwK+A64UQ+8877ovAGuAerDDMB4F/BtrsxB/BAAAgAElEQVSFEJlzjhsTQj+MME3Uo3sovPxbQCJ43R14p80fl2JSKUZygNRP/5HY3R+uuIiV0BQrGicUR6qrLPpJCEFB1UkWVCQJ6gLecWHhCyFQdJN0UUXRDGJnNlsrdUWJfMrKX2iajBSoLGvVLBVI/egfCN3wNnwzFlU013hF7z9NfvNTGAOnCVyzFv/ClUiesdf7daSFPg58m9fi6P9MCPEjSZImAa8Cc4UQpyVJCgJfB+4CAsBh4DNCiKfPm0+YpRwggew6+3O5b1ohTNRj+yhseRLJ7SW0+k487dMv6zldDpQju8mv/zl193+8YmtGGBpm33EktxepcWLFiW3Dgp8uquimIOL3EPF7HJcHGGlMIcgrGpmihikE0UCVBF4IRLoPkR1Cbp5aVqGy181nGGR+/k3cTe2O20teCRipQfKbnkDvPkZg+a3451932QM1hBAgTDAN62f4d5cH2esfX5mxetdB6+SFCYZ+5o24we1FcnvB7QOPzwoT81SWIu8UIUyUgzsobHoCV0MLodV3jUhnnbFMYetvUY+/SuxdH604ZEyYJiJx2kqqap5aNUtJ0Q2yJY28ouFzuwj5PAS97stW68YUgpJqkFM1iqqO3+Mm4vdUzdUkTMMqUmZoyE1TKxYkIQT55x/DyKWJ3vWBUaucOhYwizkKW55GObSDwDU3EViyZlQteCEE6CqoRYRWAl1FaIr1N0MHCZCt0gdIEkgyUrgeV7RxfAn9+a8phgVfVxG6euZDKCHUIhiqJfa+kFW3wxcalaeu0HVKe16k8PKz+OcuJ3Dd7cjesdPAeCQRQpD77Y8wizmid36g4hAyIQQiO4RI9SDVd5QdfnkhzDNWfl7RKWo6PpcLv9dFwOPG55ZHtCOYdiaxqqQZlDQdj8tF2Ocm5HPjqqJwCqWAOXACKRBBqm93VDH0YuQ3P4l67FVi937s6rmuTZPS3s0UtjyFb9YSgivehBwYuY5Wr72uAUoeUcojlDwoBUvEvQEkj98yat1ecHvB5bnoQ3fcVa908prCNEEtIM58UCh568MIRq1wMt/Ilqg1C1nyL/4KrfMwoTVvwztzyWV3M40GwjTIPvF9ECaRtzxUlYqBQilgDp5E8gSQGjoc9Z61g5UEZVBUdUqagWaaeF0yPrcLr9uFxyXhlmVcsuSs36oQ6IZAM01U3UTRDVTdRJIg4HET8LgIeF1VFffh1xapXstV09BRcWTNMIWXn0E5sJ3YPR8tO5x2vKH1dZJ77jEkj5fw2neOaNavEAK0EqKYRRTSoBYtUfeHkXwh8AXLuvavaKE/HyEEKAVEMWN9iIaOFKqzboIRFH2t+zi55/8LOVJP5Nb7xtRu/EghDJ3sb74LYIVdVmElJUwTkexGFNLI9e0QjI3Yd2aYAlU3UA1LnHXDRDcs4XbJErJ05kcGa71sYZ4Rd9MUGEIgAW5Zxu2S8bqHHxzyiO4NCKWAOXQKXG7khknV+eyFOOOy2E7dPR+7Oq5hXaOw+UlKB14htPoufHOWjdwqTysh8ilELgnCfM0Y9Ueq4hq7qoT+fISmIPJJRD4JQiCFG5DC9SPi3hGGTmHrbynt3Uz4xnfgm7206q8x1hCGTu6ZH2FkU0Tv+mDVkkVEKWcJmduLXN8xqj5SUwgM8zUxN8+7Hl97AFj/HU2/vzB0y4rPp5Dq26yopar4+E3yLzyO1ttJ7B0fvuw15kcDra+T3NM/wtUwgfDae0Zk9SJMwxL37BAYKlKwDikUt6z28VLrZiQYqfBKIYS1uZEdRBTSSP4IUqzJWipVGesC+iHu5nbCN9+H5B17oVjVRAiT/IZfonUeIvq2D1Yt1loIE5EZRKT7rAd03YSrtuS0EAKRG0Ike5FCMaS61qq5toSqkP3tDxFKkcidH0D2Xdk+eSFMiq88T3HHesI33T0i7lahKYjMgGVg+kLIkQYI2C85XA41oT8PYRqIXAKR7gePDzk2AfzV7VglNJXcC4+j93QSeev7rvjIHCEEpV0bKWx7lsgd78E7cUb15tY1RKrHekBHm5GijVeN4AshrBVpqtda3cTbKg6bPBcjPUTm1/+Bu7mD8Np7R7U2y+XALBXIPv0oolQg8pb34opUb+MfrGRAke5HFDOWcRJttDZSR4Ga0F+EszdRug8kF3K8teIEk/MpvbqF/Iu/JnzzPfhmLq7q3GMR9dQhsk89SnD5rfgX31Dlh2cJkepDFLNI0SakSEPVN2zHCkKY1pI/1Wf54etaqn5tnv2urr0V/6LqfldjEX2gi8yvv4N32gJCq++qastBoZUwkz1Qyl+2a7Mm9JfAEvwUItUDHr8l+BWUcj0ffaCLzC+/jX/hKgLLb7nibygjPUTmN9/DFY4Rvu3dVQ9RE2rJSgwqZiwfdbRpTGYqloMwdMu9mB06s9pstjbrqvnANHQKm59EOfAK4dsfwDtxZtXmHquoJ/aTffqHhNe+E9+sa6o2rzA0y/jIJ8+sNpsuW85BTehtIoR5Jp67z4rUibdWzUVg5NJkfvkt3E3thG++94pqYHwhhK5T2PwEysEdhN/0O3gnOW8yfunX0F4TRa/fWioHY+MuuUcIAaWc5U4sZqz3EG2qqrExjJEaIPvkfyIFw0Ruu/+q2HQt7n6RwtbfEr3z/Xhap1RlTiv3YxCR6n2tjMdlXl2OO6FP5EvISEgyuCUrrnn4ZzSsYWHoVohfMWvFJwdj1ZlXVcg88T0kl4vIm993xftDAdTOg+Se+THeKfMIrr4T2Vd98RKmiSikEbkEqAVLKIMxCESqkjw0EpwNAy6krQ072WUt90PxEREMYRqUdm6ksO0ZgtfdgX/R6it+ZQlWFnfpwDZi73i4ekECatHKQpZk5IaJSKOUUGaYAt00MczXosKEEAgBPo+V/T2uhH4oV0IgME2r+YL1BgUCgccl43XJeN1WizfvSGY3lnKYg6eQvNVL4BGGTvbJHyB0jeid77/stTNGA1MpUnjx16jH9xG66e4RLY4ldNVyw51JRJECUUvwA5FR2xS76LkZumW5l7KIQsYS92DMWj2OgPU+jN5/mtxzP0Xy+gnfct9V0WdBCEFh85OoR/cQe+dHqpITcG6CmhRvtcK0R0B7rKxqgaIbKLqBppuoholAnE3oc58J7ZUkCUkCv8dF0DvOhP5ir2mYVlq5ZhgouklJs5JcfB4XQa+boNddtQbSwwjTtCI+8imrGqC/cn+zMAyyv30UoSpWCYEr3I0zjNZ1jNxzP0WONRBa83bc8eYRfT1haJagFrOIUg5k2fr+vEErcsUbGNESCOgKQilYlruSB00Bf8gK7Q1ER9wSNIt5ClufRjm0k9DqO/HNvfaqsOIBK/Hr6G5id3+kKvHxQlMwB09aQRuN1UlQOxfDNCmoBoUzWdvD4u1zu/C6ZDyuS2dsjzvXjZPXNExBSdMpqFZquyxLhHxuwj5PVUVfFDKYg51WuFRsQsU3jDAMMr/6NnIoQvjW+6+aG1AYOsVdGyhuex7f7KUEr7t9VDrynE07L+XPlMwogK5Y9UM8fmsz1+W1bmCXxyqiJ8kXrJz6PyoI6hrC0MDQQFOsQlSaYo0dTmn3Bc8kyYy8K0kYOqXdL1HY9iy+GYsIrrxjVGq2jBVKezdT2PYcdff9QXUs+TNln6XYmc3WKt2rhmlVMc0pOqphEPBYxmrA48JdhnZd0UJ/LsP1vXOKRl7R8bplIn4PoSrVJhe6ijlwEmSXZd1XWlZXVUj/7F/wTplL8Lo7Kj6/8YRZyFHY8hTKkd0Elt5EYNHqUY+cEaZpif2wOJ8r2MNVU02Dc8sfnBl59iGA7LJqKw0/IDw+6314/KMe6y+EiXp4F/nNT+KKNRK64W1XfP7G+agnDpB95kfU3fsxXHXlNaIf5qyrJpdAbp5SleRKS6MMMkWNgqYT8LiJ+Dz4va6Ky1RfNUJ/Lq/VJtcwTLOKNb9NxNBphFq0yupW6Pc18xlSP/4qoZvehW/6gormGo/oQ70UtjyF1n2c4PJb8C+4fkztW1jXorBa6wwjjU5QgF2EEKjH9lLYbPVKCF7/ZryTZl/u0xp1jNQgqZ/+I9E7H8LTNq2iuYRpIoY6Ebpq3eeuyss+D/dKMExBLOAl5PNUtXzGVSn051LSDNJFlZJmUBfwEglUJvhWg4d+RHYQecK0ijfStN6TZH7xLWL3/cGI+63HKvpAF4XNT6H3n8J/zU3456+84lPxK0WYBuqR3RS2PQeSRGjlm6/adpdCU0j9+Ov4F62uvNWloWP2H0dyeZAaJ1UUrvta9zMFWZKIjWD3s6te6IdRdYNkQUU905czVGFfTjOXRCS6LLGvMC29uPtFlH0vE7vvD6+azdkLofefpvDK82inDuGfvxL/olVVT1Mf75hKCeXAyxR3rEcO1xFcdvNVK/DD5NY9jlAKhG9/sLK2lIZutbj0h62m6hXMVdIMEvkSQkB9yId/hPsZ14T+PIqa1VBaQqIx7MPrLl9Yz/bnnDC1Ih+eEILMz/8NT+vkq85ffyGM9BDFnetRDryCp2MG/kWr8XTMuKrFTE/0Udr9IsrB7Xg6ZhJYelPVEoDGM8O5GnUPfrKiPA1haJi9R62Q1wr6GBumIJEvUdSq0+jdLjWhvwBCCLIljWRBJRbwEAt4y/4yRCGNOXiqYsveyKVJPfr3xO756FW3iXYxTLWEcuAVSrtfBNPEN/dafHOX4wpXJ4ltrGOqJdTDuyjt24qRHsI//zr8C67HFalOk5HxjtAUkj/4W8K33Id3cvn7EsLQMXuPIAVjyPHWsufJKxpDeYWQ10086EMexRLWNaF/AzTDZDBXQghBUyRQdkimyKcwE13ILTMqih4p7tqIcmQ3sXf9/lVtvZ6PEAK9t5PSvq2oR3bhnjAJ36wleKctGJXwzNFE6DraqUMoh3aiHn8VT8d0fHNX4J0y96p2612I/Iu/xswmibz5PWXPIUwTs++I1Y60THeNKQRDuRIlzaAp4sfvGf2s93En9Du6UnhcEgG3i6jfQ9TvxlvlRKhzEUKQKWmkCipNET9Bb3lfkpkZQGQGkVtnlp1FK0yT1I+/RnDZ2qoWX7qSEJqKemwvyuFdaKcO426fjm/6ArxT5o7brkimWkLrPIR6/FXUY6/iamjBN3MJvpmLr4p6NOVgpAZJ/eRrxB/8ZNnfuxDC6rcrydbGaxkir+om/dkiPrdMQ9hfcWTfG2GYgqyiky5p5FWrHaZmCFrCPibGg+NL6J882He2sXKmpJNRdLwumZaIj9aIn9aoj/ZoAK+7uuJf0nT6syWi/vJdOebQ6ddCssr8wtXOQ+TWPUb8PZ+6auqul4uplCxxPL4PrfMgrlgjnilz8HTMwNMyeUyFap6LME2MwW7U00fQOg+i95zE3ToZ79R5eKcvumpcU5WQfepRXHWNBK+7vew5zFQvopixVuJlJLMVFJ2BXIn6kJeIv7olNgxT0JMt0ZMp0ZtV6MmWyCo6Ya+bmN9N6EwlAI9LYlp9kGkN4fEl9Oe/phDWU6w3p9CTKdGTUejLlWiN+pnZEGZmY4iwrzpLJd2wns4el0xj2O9YrIUQ1q69L4gcL6/BsBCCzM++gW/OMvzzVpQ1x9WIMAy07uNonQfQTh9FT/TiaZ6Iu3UK7pbJeFomXTbrWKgKWv8p9N6T6D0n0bqPIQfDeDpm4pk4E8+kWcijVBzrSkBP9JF+7J+Jv+/TZYfhikLaCqRonVWWQZApqqSKKs2RAH5PdQwyVTc5mshzZDDP8WSBOr+Htqj/rJFbF7h47P24c93YeU1VNzmeLHBkKM+xoTwdsQCLW6NMqQ9WvHQyhaA/U0SSJJoizpdiwtAxuw9aNTHKbBahnjpCft1j1L3nk2O2AuNYx1RK6D3H0XpPWgLb24nk9eFqaMXd0IKrfgKuaANyrB45VHl5YyEEopjDyCQwMwn0RD/GUA/GUC9GLo27sfXsA8fdNq1mtVdA9rc/whVrILjiTWWNF7qK2X3IWnn7nUXLCSFIFVVyJY2WWLAqpVZ6syV29WQ4OJCjPepnZmOIafXODNgrUujPRTVMDvRn2dWToaAarJgYZ1FrtKKsMyEEA9kShhBMiAaci30xiznYidw2uyx/vRCC9E++RmD5rfimL3Q8vsb/RAgTM5NEH+q1xDfRh5EZwswkMEsF5EAIKRBBDoatMD2PF8njtbIiz/n+ha6BriI0FaGWMAs5zGIOs5BDcrtxReuRow244k3WA6WhFVddU20jtUoY2RSpH/69Zc2XsRF/dtXtDyPXOYtuE0KQKCgUVYOWWAB3hclUxxIFNp1MkFcNFrVGWdgSLds7ccUL/bl0Z0q8dCJBoqiyanI98yZEyrbwhRAM5koYpiX2Tt04ZqILDB25aXJZr68c2kFp72Zi7/r9ssZXAyEEWjqNns6iZTIY+TzuSARvPI6nvg6X/8pwNwhdOyvWopjDLBVeE3Nde/3BLheS22c9BLw+5GAEORBGDkaumEbwpqajpVKoiSRaMoXs9+GJRnFHI3jjdZf1oZXf9ARCLRG+6Z1ljTczg4h88oxf3tk9ncgrFFWdlliwIkPyVKrI+uNDqLrJ6in1zGgM1WrdlMOpVJENx4fQTMHtM5tojZbpxxOC/mwJCWiKOPPZC9OwXDj17WU1LxGGTuLbXyB278dGtTSCEILM7r30Pf0sA888j5bO4KmL4Y5GcQeD6LkcaiKJmkjiiUUJz5xOaMZ0IrNnUrd0CYFJHbXQ0HGEMjhEavsusvsPkDt8lPyRo5R6evHEYnjq43jqYpiKip7JoGWyYJo0rl1D820303DDKuRRDCUUhkHyO39F9O7/VVauieWyOYjcMtNxmeh0USVbUmmNBXGVaclnFZ1njwzQn1NYPaWBuc3hqkXpXJVCD5Zg7evPse7oIAtaIqyeUl/WUssUgt50Eb/HRX3ImcUmilnMoVPIbXPK8gHnN/7SqmOy+i7HY8tB6R9g9598Gi2ZZMJbbqf51rWE58y6oHALIVD6+skdPkLu8DGy+/aT2rELoenEliwift1yGlauIDhtSk34xxBK/wCJzS+T2LyV1PZdaOk0scULiS6cT3jmDMIzpxGY2IF8kQ5ope5e+p9bR9+Tz6D09rHwK18itmh0CvIpx16l+Mpz1N33h2WNN/qPI3kDjl02w4lQrWX65IUQ7O3Lsv7YEItbo6ycHK/I7XMhrlqhHyav6jxzeIChgsY75rXQEHIeBmWYJt2pgpXS7He2Q1/uxQVnGov/6j+Iv//PR1ws03teZfcff4qOd9/DlIc/UPbrlbp7SW3fSWLLywy9tAUQNKxaScOa1TRcvwJ35OqpjT4WMFWN1PadDG54kaGNm1D6B4mvWEbD9SuoW7aE0PRpZW9EDzz3Avv+4q+Y9af/m9a3vbXKZ/4/yTz5fTxt0wgsWu14bLlGl6ob9KSLtEQD+MqIrilqBk8c7COr6Lxl9gSawyPj3rvqhR7OPFF7s7xwfJA7ZjUzs9G52Ax/4a2xgKP6OEJTMHsOIbfPcVzuVAhB6gd/Q/i238HTWp6v3w6pV3ay6+OfZO7n/5zmW9dWbV4hBIUTJxl6cTND618ktWM3kflzaFp7I003ryE4eVLVXqvGa6hDCQbXb2Rg3QaSW7YRnDKZxhtX03DD9UTnVzfDNnfkKLs+9idMfN8DTHrw/qrNez5C10j8+yPWJqzDrlFCCOsejE1ACtkvH2Gagq5UviwDD2Awr/D43h5mNIS4aVpjVcsSn09N6M+hJ1Piv1/tYWl7HSsm1jm2WrMljXRRpa3OWRinOXQaJAm5vt3pKZN/8Vcguwhd/xbHY+1Q6utn633vZf6XPk/D6pUj8hrDGIUiia3bGFy3gYF1G3BHwpbor11DbMnCWmRKmQghyB89bn2uz68nf/QY9ddfR+PaNTSuWYW3fmQrgBa7utn23g8z7wufHbFrSD2x3+ocde/HHI8V+RRmus+KmXdw3w5ki1bxw4jzPb6jQ3mePNjP2ukNzJ8w8hnbNaE/j6yi8/jeHtqifm6b0ehsg/VM2KVLlmgI2//yha5hdh+wlo0OkzO07uNWpuwDn3A0zi57P/05/C0tzPj46Eb3CNMks3c/g+vWM7BuA0r/AI1rVtN0y400rL4eV3DkGmZfCZi6Tmr7Lgaee4HBdRswNY2mtWtoXLuG+uuWI3tHtxn64PoXOfTlr7DyFz++qH+/EnLPP4YcjRNcdoujcUIIawM23uooKCKnWGVRnBp1AHt7M6w/PsQ75rXQHhud67gm9BdA0U1+uruLloifWx2KvXFmOdfssHiROXTaakPosDqeMA0S3/wL4u/7s6pndhY6T/Py776f1U//HHeo8lZplVDs7mHw+Q0MPP8C6d2vEl9+DY033UDjjavxt9aqeQJomSyJlzYz8MJGhta/iL+tlaabb6Tp5hsvumk+mmx738N03H8PLXdWv9R24rtfInrnQ7gbnWWci0IGM9lt5bTY/HwM06QrWWBCGX75fX1ZXjg2yLsXt9MQHL2H7bgT+u9tOEbE72ZCzM/stqjjSBe7KLrBT3Z30xELsHZag6ObJK9YJY7b64K2x5311XfMc1zDJvPLb+OdtQT/7KWOxl2K/X/5Zbx1Mab/0eWL1b8QWibL0IaXGFy/kaGNm/A1N1k+5htXE1u8cEQsxrGIEIL8kaMMrrc+i+z+Q9QtW0LjjatpWrtmzD0ABze8yJGv/H9c9/h/VvWhY2STpH70Vep/73OOM8WN3iNI4XrkcL3tMQPZIrLkbNUOcKA/y3NHB3n3onYaywj6sENB0TnUm+VUokC2qJEtaiyeHOf6mU1lC/0l7yZJkuqBbwFvAgaBTwshfniRY6cBXwduBBTg20KIPz3/uL5MiSN9Gt3JIgd6MoR8bua1xbhpbjNr5zYTq9JT0ud2cd/CNn64q4uXT7tYMdG+HzPodZMtaWRKGrGAvfORPD7whRD5FFKkwdG5eibOQO86ClUUeqNQpO+Jp7n+Fz+p2pzVwhON0HLnHbTceQfCMEjv3mu5Br709xS7eqi/fgUN16+gftV1BNrLqyk0VlFTKZJbtpF4aQuDGzchuVw0rlnFlA++j/iK5bgCYzdJreGGVRz68ldI79pD3ZJFVZtXO30ET8d0xyIv1BJoJUcbsCXNoKgZdMSdrXA7UwWePTLIfYvaqiryimaw6cggz+/rY3dnit50kenNESY3hogGPUT8btyuCpOtLmXRS5I0LOofAq4Bfg2sEkLsO+84L7Af+EfgXwEDmC2E2HPeca9z3Qgh6EoW2d2Z5Ll9fWw5MsSCiTHuXjaR2xa0VGUXO1PS+MGO07x5VjPTGux/ucNROB3xkO3zEIU0ZqoXV5uzJgl6/2myTz1K/L2fcjTujej51RP0/upJrvnG16o252igDAwytHETiU1bSGx+GVcwSHzFMuLLlxJfvhR/29iyci+FlkqT3L6T1LbtJF/eTuHkKeLLr6F+5bU03LCK4NTJl90l44Rj3/gWav8Ac/7iz6o2Z/aZH+Nuaiew+AZH48xEF0iybXepEIKedIGI30vEQZRNqqjxnztOc9fcCUyOV6c/ws6TSX68+SQbDw0wuzXKrfMnsGxqPVObwheM5R8x140kSSEgAcwXQhw587fvAt1CiE+fd+zDwINCiJve8AUv4aMvqjobDg7w6EsnSBc0PnzzdO5Y1Fax4J9OF/n5q728d2kHUQdf8GCuhCxBfcielSWEwDy9z3FTcWEaJP71s8Q/8H+r1mhj5x/8HybcceuoxD+PFMI0yR0+SmrbDpLbtpN6ZQeyz0ds8UJi1yyibvFCwrNmjPrG5MUQpknhRCfpXXtI79pDauduSt29xBYvJL78GuqWX0Ns4QJk79gsr2yHwqnTbHvwQ6xZ90TFheKGSf7gb4jc/gDu5g7bY4QwMU+9akXa2GwGlFd0UgWFNgcuWcMUPLrzNHObIyzvqLzz17bjQ3zzuSN0J4s8uHoKty9spcFG7H0lQn8p180sQB8W+TPsAtZe4NiVwElJkn4DXAvsBf5QCLHXyQkFvG5uX9jKmxa0sPXYEP/67BG+/cIxPvvOBSyeVH4IWUcswPKOOn59oI/7F7fb3mWvC3jpSuWJBby20qIlSUIKxRH5pCOhl2QXrqZ29IHTeCfOsj3uYpiqSvLlV5j3hc9WPNflRJJlIrNnEpk9k4kPvvts3H565x7SO3fT9dOfUew8TXDyJCJzZxGeNYPglMmEpk7B3946Yr5+IQRK/wCF4yfIHz9J/uhxsvsPkjt0BG99HdGFC4gtWUj7vXcTnj1rVMsIjDTBiR24Y1Gy+w4QXTCv4vmEqmBkkrgaHLb4K2bB47ct8kIIUgWFuqCzXhQbjg8R8rpY1l5ZNdKeVJEv/eJVTgzk+b2bp/OWxW1VqYxph0tdfWEgc97fssCFQkM6sB4AbwOeBf4Y+LkkSXOEENoFjn9DJEniuumNrJjWwDN7e/nEozu4c0kbH71tZtnNvldMrONEssCWziTXT7a3ceN2yYR8HtJFzfamsRSOY/YdQ9S1Orqg3M0d6H3VEfrUjt2Epk7BG7+yeo9KkkRo6hRCU6fQ9s63AWCUSuQOHyW7/yD5o8dJbNpK/vhJlP4B/BOa8Le14W9vxdfUiLc+jre+Hnc0givgxxUIIPt8r1mmQmCqKkaxhFEsoufyqImEVftncIhSTy/Frm5K3T24QyGC06YQmjKZ0LQpNN9+K5E5s/BEr/yOUQ2rr2foxc1VEXp9sAt3Q4vjHAuRTyKF7Bt/Rc1AgKMOc53JAvv7szy0vLzuVGA9YH6xvYuvPnmAB1dN4e8fXDpqAj/Mpd5xDjg/EyCGJfbnUwA2CCGeOvP730mS9H+BOcCeCxxvC0mSeNPCVpZPa+Dzj+/hoW9s5u8fvIa2MvxkkiTxltnNfO+VU8xpChO3uekbC3jpThWoC3rtrQQ8fqvsrVoEB83E3Y2taB72pQ8AACAASURBVKcO2z7+jUjt2EV8+dXRqtDl9xNbOJ/Ywvmv+7upqpR6+ixh7upGGUpQPNVFetde9EzmrJgbigLnuBNljxdX0HoIuEIhvA31eOvjhGdOp/GmGwi0t+Jva8MdurJ62Tohfu1Sun7yeFXm0gd7cDU6DEkWJqKYRY7bT1DMFFVHneV00+SpQwPcPquZYJmNR4qqziOP7+FYf45vfug6ZrZcHiPgUkJ/CHBLkjTjHPfNYiy3zPnsBs4WqJDe4NN85JFHzv7/2rVrWbt27SVPNB7y8g/vWcqjL53goX/dzD89tJzZrc6z0aJ+D9dNivPs0cH/n733DrPrKu/9P3vv0+v0olHvsiSrWJZsy7IlF7oBU4Ih9EAuSUjPhfRw87vpCdyEAAECAUIHY3oxLqq2ZNmSbPXep8+cXnZb6/fHnhGDIlt7n3NGmhmdz/PMIxjvtc4+Z87+rne96y28abm7aA6/phL0qRR001U7MUVRUCJJZCmL4kHoteZOSvu2ur7+pcgdPkr7y++ryVyTFTUQIDJrBpFZM673rUw5Ejct5sjhozWZyx7qxefVbVMugC/oOjnRsGwMS9CecG/N7z6fpjUWYJ6HAI6xpIsGH/zCs8xpi/Hl37jDc7z+5s2b2bx5c0Wv/T+QUr7kD/A14KtABLgTSANLrnDdQqAA3AtowO8DxwHfZdfJann0hW55z988Jg+cT1c03rKF/MzOM/LscMH1mIJuyoupvOvrRTErre6jnu5L6GU58IkPSyFsT+OuxI5Xv1Hmjh2vep46da6EEEI+sfZuaaQqewbHkn74k1I/e8TTGHvogrRTPa6vH8yX5FC+7Pr6gm7Jj28/KVNFw9N9jTKUK8s3/+s2+f9+clgKISqa43JGtPOqmn2lHzeOot8EwkA/8GXgA1LKw4qizFQUJacoyvQR9T4GvB34D5xInQeA10oprVosSGO5f3knf/HgMn77S8+y/3za83hNVbhzThNbTg+NLj5XJezXsGyJYdnuXiQYBaOMtN2/fSUQRA2GETnv72kswjApX+ypFxSrM26MnpUUTp2pei47NYDW0OppjCzlUELu3CBSSgply1M45c5zwyxui9MQ9h4dNZzXed9/7mLTTe38zsvdZ+uOJ1cVeillSkr5oJQyJqWcLaX8+sjvz0kp41LKC2OufURKuUBKmZRS3iOlPDxeN75xSTt/+eAy/uirexjM6Z7HL26NYdmSM6mSq+sVRSEa9FEw3Am3oqqOf14veLovNdmCnRn2NOZySt3dBNtbJ0zIYZ2pSWT2TIpnz1U1x2jnLzXmPmhA2hZYhuvzr7Jpo2mK6wPQgmFxsC/HbbO8R/lZtuBDX9/HxiXt/MZ9CyaEyIMLoZ/IbFzSzoNrZvDhr+/FtIWnsYqicOuMBp45n3I9Jhr0UdA9WOjBKNKj0GuJJkR2yNOYyylf6CY83XsVzTp1vBCe3kXpYndVc9i5FGq80Vs8vl6AoPs4+IJhEfWQt7D3YoZFrTFiHqJzRvn4o8cIaCq/dX/1kXO1ZFILPcCvb5pP0Kfx+S0nPY9d0hZnuGjQn3e3Iwj6NISQrhcVJRRF6kVP96QmGrFz7hefK1Hq7iE0zePhVp06Hgl3dVYt9CKbQot7CwGWehEl6O6AVEpJUbeIumzIbQnJ8z3ZihKjdp4Y5NH9PfztW1aMa136Spj0Qq+qCn/1hmV8Y+c5jvZcHvL/0miqwvKOBPt73Y1TFIVwQKPk0n1DIAJ60fU5AIAWSyLyGdfXXwm9t49g+7XrQVvnxiTY3o7e11/VHKKQ8eS2gVGhd+e2MWyBouDabXNiME9LNECTx3pb+bLJ/3lkP3/x4DIarmFFS7dMeqEHaE+G+b1XLOKvHzngSVQBlnUkONyfQ7g9lA34KJnuDmQVzQeq5vgTXaJGk4iCtwXrcvSBQUJt3g636tTxSrCtFb1/oKo5RD6DGvOYcWqUwGXWecmwCXtwwRzsy7Gsw3vY9iceO85t81q4Y8HEfO6mhNADPLCqCyEkmw97szAawn6SIT8X0u4OZUM+jbJpu19QAmEwy67vR43GEcUr5aO5xxgaJtDirXpmnTpeCbQ0YQxV52YUxZynHgxOFJsEly07dcsi7DJ+XbdsLmRKzPcYN9+bLvHjfd389ssmll9+LFNG6BVF4X/dO59PP3Hcs1W/oCXKsUF3h6Y+TUVVcO+n94eQhrtFBEAJx5C1EPpxbi1Xp44/kcAuFhCG5wonlxDFvLf+sEbJqW/j4iBWSknZtAm6LJlyarjI9GSYoM+bLP7X1lO8Yc10msapKXgtmDJCD3D34jZ0U7D3rDcrY25TlDMp94emQZ+GYbmM8vEHwXQf/qmGooiyN7/+5ZiZDP6GqVXjps7EQ1FVfIkEZqbyMyVZLqCE3FvQ0jJcFzGzhERRFHwu/fNnhovMbfJmzefKJj95vpu33THb07hrzZQSekVRePO6mXxjp7fY3tZoAN0SZMvuLJOAT0V3mTil+AJIDz56xT9ykGNVbiWZmRz+5Pg3K65Tx59MYGUr34GKctFbWW5TB587oTcs27V1LqXkbLrErEZv/V9/uPcity9opTUxcZvFwBQTeoDXrOpix7F+b/HuikJXMsTFrDtfesCnuY/b9wc9HcYCqKEIQnfv7hmLlBIrn8cX97AdrlOnQnzxOGaucqGXegkl6EFcLQN87qJaDFvgd1kRM6tb2ELS6DET9kd7u3lwjfsa+teLKSf0ibCflbOa2HbU26FsZzxEj0uh92uqe6HXfGBbnlwxSiDktEirALtYQg0GPJd8rVOnEnzRCHbBW67IWKRR9iT00jZdFzIzbeE6rLI3p9OZCHrKZO1OlbiYKnLLHPe9aq8XU07oATYtaWPrEW9C3xYL0p93Z3n7VAVLSFfirSiqE2LpseaNNLyXdQCwi0V8kRu3fG6da4sWjWBVKPRSSqShu/a5A2CbriNuvAh9f16n3eNh6vaj/WxY1HbNa8tXwsS/wwpYM7eZ504Pe7KimyN+hkvuhF5RFLQRsXeF5gPhobabL4A0vbl7RrHL5QndXLrO1EILhRB6ZbtPbBsUxdvu07ac58nV9BKfywzV4aJBs8dEp+fODLNm7sS35mGKCv3M5ghCOK273BIP+jAsge4ymsanKtjCpfvGq0Xv83v2648iymXU4MQN86oztdBCIexSZUIvLcO1GwacZiNICcrVZUtKiS2l61IEwyWTxrA3od97JsXq2XWhv24oisKCjjgn+/KexsSCPvIuyxtoqort1qJXNZDui64pPr+n8sZjEYZZr1pZ55qhBAIIs8IIMdsCD0KPEKCqrvzoQkpURXHtc8/rFvGQ+wzaXMkkr1t0eYzSuV5MSaEHx6o/N+StcmQs4CPvMlpHVXBdNkFRNaRwWcceQNOqEHqjLvR1rhmq34c0Ktt9SttyyoS4RdiO0eQCW0jcus5NW2DagrCHRKlzQwVmNruvoHm9mbJC35oIMejycHWUkF+l7NJ1oyoKbg16FOWXepJe9XJVc6yXCpC2XY+4qXPNUDQf0m0znssZsdBdI4Urtw2MeHhcirBuCYI+zZNoD+R02iZ47PxYpqzQJyN+skVvW8qApmK4LW2gKO4PexXVk+sGRXWslwqQtsC1KVOnTpUomoqs1CgRthOV5nqAdIwmFwgkCu6uNWxBwGPZg2zJJDkBq1S+GFNWEcIBjZLpzf2hqYprv7sCeCpS4KWkgccdwOWv4+nhqVOnGpTKhd4ZP06uD/drAraQ+DzeR9mwCfknz3M2ee7UI5V8fSaHt61OnYnDJHFRX50K3ofbHcNEYMoKvSUkmhf/HyCk+7+3Z3vb0xPhwRy54vDKC6LVqeMF6cGd8iIz1OxeKp3a2UB7uw9VVbCq2clcY6as0KeLJkmPdStMD746KSWq22VBSjyZDKLyh6can2mdOl5xDv8rkxFFUZGuIxrw5NJUFAXpUun9mophexP6ZNhPplR54cFrzdQV+oJBQ8Sb0Ou2IODySyvxoMVSeBNu6T6M7HIUVUPaFUZB1KnjFSGcKLFKUL0GKXgRelxHxQU11XWi5CgN0QCpQmVhpdeDKSv0F4aLdDV5q/lSMGyiAXdfWiEkqsusOym9PQzSsit+eBS/H1lpAkudOh4RpoXq9xALPxaPGeMommMEuUBTFNd5LkGfk/zoulAh0NUY4cJQ5cXcrjVTVuhPD+SZ1eKtiUBet4i57C9pS4nm1kr3GC8sPdTzuBw14K88U7FOHY8Is/JMbMXn85YYqKqu80tUVUG4LjyoEAtqrrPiATqSIXJli7zLHhbXmykp9LmyycVUifnt7muy65aTHefWoncy79wKvQWqB+G2TRS/N7fTKGooiNAnz5ayzuSmmtpKis+P9NJgR1FBSqfmzVVQFQU8uG+SIT9pDz53VVVYMi3B/vNp12OuJ1NS6PedTbFsepKAy16R4FSva4z4XfeitIRwH9VjW5587tI0ftFpyiNaMIhdrrCaYJ06HrHLOmqowiJ6Pj9YlivhhpFMV829u8enqq4LDzZFAgx7TLC8ZU4Tz52urjn6tWJKCv2OowOsm9fiacxAwaAl4u4LK6REwal3czWklJ5Kq8KI0Ltsl3Y5WiSCXZw8vsM6kxu7WEQLV1bYS1FU8Pu9leRWfR6EXnHtd2+JBhgoeOsBcdv8FnYcG/A05nox5YReCMnjh/q4b1mHp3G9uTIdcXfiOtrQwFVtDGE7Ffe8WPRGGSVYWR0NLRrBLpaqai5ep45b7EIRX8zbWdhY1EDIW5MdX8BpPuICpxOcu+egMx6kJ+dN6FfOamQgV+a8x+KJ14MpJ/TPnBqiORbwfBDbnS3T6bJIkeGhcw2W4bojzijSKKMEKhN61edDCfixi5X1nK1TxwtWvoAvWrnQK4EQ0kN/ZMev724H4PepmC5DjVujQTJlk7KHAm2aqnDv0g5+vK/b9ZjrxZQT+m/tOseb1s70NKZgWGR1y7VFb1jCvf/fMpwG4S6Rwnbaq1Vo0QP4EwmsbLbi8XXquMXMZvAlExWPV0IRpO7B1egLum7KE9Q0DJfx8ZqqMC0R4ryHZkUAb1w7g+88e95TaOb1YEoJ/cXhIs+eHuZVK6Z5Gnc2VWJGMuyc1LvAsGz3GbSmjuKyaz2ALJdQgqGqCpP5kwnMTF3o64w/ZiaLvwqhV0MRRMm960PxBZCmOxeLY9EL1/H0sxoinEl5E/qFHQm6GiM8cbDP07hrzZQS+s9tOcmvrJtJJOgtBv3EUIH5ze62n0JKjJH61a4wy+B3b52LUh417D4s9Er4GxswhidHNECdyYtdLIGQaFU0o1fCMaQHoScQcp4pF6iKgt+nYrh0x8xviXJiMO/5fOs9d8/ls0+eQHgp53CNmTJCf3awwJOH+nj7+tmexpm24MxwkXkuffr6iDXv1vqXpjd/uyjmUSJx19dfiUBzM8bQUFVz1KlzNYxUikBTY1VdltRIHFHMuR/gC4Jtuu7YFvJplE131zZHAgR9qudD2TsXthIJavz4+Ynrq58SQm8LyV89/AK/fs98z80Ajg8W6EyEiPjdWeglwybkMuVbSjFi0bsPPxOFDGq0OqEPtjajD9SFvs74ovcPEGxrrWoONZpAFNy7GRVFcXbIhjurPhzwUXIp9ACL2+Ic7POw8Izc04defRP/76dHGMp7WySuFVNC6L/y1Bl8mspb1s3yPHZ/b5blHe6FtWRahF1mz2KUwRdE8VD+QBQyaNGk6+uvRLCtDb2vv6o56tS5GjUR+lgSkc94GqMEIkjD3QFuyK+hW7ZrP/2y9jhH+nOeD1eXzWjggdXT+dvvHZyQoc1XVSBFUZoURXlEUZS8oihnFEV5q4sxjyuKIpRr0OrohXMpvrD1FB95w3LXRcZG6cvrDBcNFrS484lbtsCyBSGX/nmpF1GC3vyXIpdGjTd4GnM5oc52yr29Vc1Rp87VKHf3EOxor2oONdaAnfN4nhSMgMtIHVVRCPo0Si7r2CRCfqYnwxzwaNUDfOCe+ZwfLvLNXec8jx1v3AjxJ4Ay0Ab8KvApRVFuerGLFUX5VcDHuHYUcBgu6Hz46/v4yweXMd1jpUqA3edTrO5qcF2zpmBYRAI+9z5JvQBBbzHGdnYYNdHkaczlhKd3Ubowcf2FdaYGpQvdhGd0VTWHlmhEeBR6JRhF6u4PcKNBHwXdfcGyW2c0sPt8yvUuYJSgX+Nf3raKTz9xgufPTaxgiJcUekVRosAbgL+QUhallDuA7wHveJHrk8BfAh9inDvzZYoGH/zCs7xmVRcbl3i3KoaLBmeGi6yc5j40rKCbRIPukp+klMhyHiXkTehFZhgt0expzOWEZ0yndP7ihNxC1pk6FM9dIDK9OqFXQlEQAlH2EEvvD4KwXSdORQM+SqblWrinJ8PEgz4OVWDVz2iO8pE3LOePvrKXoz0TJ8T5ahb9QsCSUp4Y87vngaUvcv3fAp8ExjWodLig8/7PPcPaec385n0LKppj2+khbp3R6DpM0rQFli0Juzy0ZTTW10PNGikEdnYIrcFbnZ7L8SfiaKFg3U9fZ1wpnDpNZO7squZQFAW1oRU7PehpjBKKI0vuhFhTVUJ+zZNVv2F2M0+dHcaqIGTyrsVtfOg1S/itL+zm0EVv5w/jxdWEPgZcvizlgP9xeqkoyhrgduDjtbm1K9OdKvK+z+7i7sVt/O7LF1UU2tWdLdOdLbO6y/2hZ65sEg25d9vIcg4lHPd0fyI7jBqJo/gqK1E8lujcORROnq56njp1roRVKGCm04SndVY9l9bYgp3yaJSE4+BS6AFiQT85D7XjpzeEaY4E2HuxsjLE9y/v5M9et4wPfvFZdp+6/hFwV4sTzAOX+zaSOGJ/iZFD108CvyelFGPErabum61H+vn/HjnAe+6ey9vumF3RHEJKfn58gLvntriuVyOkJFc2mdbg/hxAFjOocW+WuTXUi9ZU3eHWKLFFC8gdOUbz+ttqMt9kR9o2ZjqDMTyMMZTCzOawSyVEqYRd/uWQONXvR4uE0MJhfLEY/uYmAk2NBBobUQPVL8JTgfzRE8Tmz0PRKmwjOAZfUwf2sLfgASWcQKS6ne5tLmI+IgEfQwUd3bJd7+I3zWvhq3svsKQtTsxjEibAppvaiQZ9/PHX9/GuDXN4+/o5ngNGasXV7v4Y4FMUZf4Y980K4MBl1yWAW4BvjIj86Cd5QVGUN4349i/xkY985NL/3rhxIxs3bnzJm8iXTf71Z0fZcWyQv39oJbfMqfywcvf5NCGfypI299mn+bJJyK+5XhikbTlRAW3eUsPtoR58LdVbSADJ5Uvpe/Txmsw1WRCGSfHcOYqnz1I4fZbi2XOUL/ZQ6u5B7x/AF4s6gt3UhC8ZRwuH0cJh1GDw0s5LSok0DOxSGbtUwsrnMYZTGMMpzHQGf0OScFcnoWnTiMzoIjJ3NtHZs4jMmVVVca/JRub5F0gse9GYDE9ozZ2UDzztaYzi8zu++lIeIld/zhRFIRHykykZtMXd5bU0RQKsnJbk58cHeP3Sjoq8B2vnNfOlD9zOn3/7BbYfG+CvHlzuusXp5s2b2bx5s+fXvBLK1Q7sFEX5Gk4EzfuA1cAPgdullIcvu65tzP+dCTwDdAGDUkpzzHXS7SGhZQt++kIPn/j5MdbNb+EPX7mYeLhyi6o3V+bh/T28ffV0kiH3h6oXUgVa4yHXiVIiN4gs5dDa5ni6v+yPvkBwwQqCC1d5Gncl9IFBnn7tr3DXtkdRfRX29JzACNMid+QomRcOkDt0hNzhoxTPnCPU2U5k9iyic2YTmTWD8IwuQtOmEepor9oal0Kg9w84i8fFbornzlM8febSohJsayO+ZBHxJQtJLl9GYvlSfNHKywNMZPa8/4NMf8sbabtvU9Vz2bkU6W/8K02/9lfeXJ2ZfjBKqK3u8mds4TzL0xoiro02S0i+svcCKzoTrJxWeX6LZQv+e8dpvrTtNG+7YzZvvX0WMZcaNIqiKEgpK9oSuFGA3wQ+D/QDg8AHpJSHFUWZCRwElkgpL0gpLznZFEWJ4CwOfdJt+5gxmJbgJy9085+bT9IaD/J/37yiKisenIqTPzjcx30LWl2LPEBeN/FpqmuRB5D5FGrCeyKJ1X+B6PrXeB53JYKtLYS7ppHZ9wKNa1bXZM7riVUoknl+P6nde0jv2Uvu4BHCM7pI3ryM5IrlTH/Lm4gtnIcWqrzq59VQVJVQRzuhjnYabln5S/9NWBbFM2fJHT5K7tBRTn78P8gdPUZk1kwaVq+kcc1qGtesItBc3fd4ImAXS2T27efmj/19TeZTYw0gJaKQRYu5F1Ml2ojI9CGFcJWUqKmOVZ8uGrTG3X1PfKrCA0va+ereC3QlQrTGKmsI5NNU3nPXPO5d2sFnnjjBA/+yhbfdMZu33DaLRBXGq1uuatHX/AVfxKI3LcEzp4Z4/GAvTx7qY2FHgvdvmseaudWFGoJjlX/3YC/RgMbLFrZdfcAIYsSab/NgzUtTR/QcQ52x1FMFSjufIf3Vf6bp/X9dVe2QsZz65GcxMxkW/ckf1WS+a4kwDDLP72foqWcY3vkM+eMnSCxZTMOaVTSuWU3y5mX44tUVfxtvhGGQPXSE9J7nST3zLJl9LxBobaHptrU03b6WpltvmfDv4Ur0/uRRur/zfVZ/9t9rNmfm+58jtGQNwQUrPI2ze0+ixBpRY+4W0FGrvjMZ9tRq9EBvlqfPpXjHqumE3EbevQRnBvJ8bsspNh/qY+28Zu5d2s6GxW3EX8IIrcaivy5Cf7IvR7Zk0pMucaQ7y5HuLIe7M8xpi3Hv0g7uvandtR/LDVtPDXIhU+YtK7rcN/QG0kUd3RK0JzzUqhnuBiRqk7f4Yv3YXvSje0k88F5P416K4tnzPPuO93Hn4z9C9bAjuV6Uu3sZ3LaDwa07SO3eQ3TOLEcQb1tLcuXycbXWrwXStskdOcbwzt0MP72LzPMHiC9eSPNdd9CyYT2xRQtqtsiPJ/t+8/dpe/l9THvdq2s2Z/HZJxCFLLG7X+9pnCykEdkBtE73YdaZkkHJsOhIetOYJ04MMFAweNPyaZ505CXvpWiw5Ug/jx3oZc+ZYea0xlg8LcGSaUlmtURJhP3EQz4aogHCAd/kEvoHP7aFWMhPezLE4s7EyBtL0FThtuil2HUuxYHeLG9dNd114TJw4ua700VP/jwpBOLCIdTO+SgeShMD5J98GDXZRGR19T7PsTz7jvcz4+0P0f7ye2s6by0QlkVm3wsMbtnB4NbtGEPDNN95Oy0b1tO0fh2BhupKQUx07HKZ1O49DG17isGt2xG6QfOGO2jZuIGmdbdOSP9+qbuHXW98O3c+9oOa3p/Zc4b8kw/T+LY/9DROSuk8c21zXJcbGT13a4qGiHqIphFS8r2DvagKvGZJR83EfpSibnGkJ3vJ+D0/XCRXMsmWTN68bia/fs+CySX01+o1n72QZu/FDA+t7CLu4Q8qpaQvWyLk12hw2TAcRg5hi1m09rme7zX1pb8n/oq342ub7nnsS9H/+GZOf/rzrP3GFyeEtWgVCgxtf5qBJ7YwtO1pQl2dtNy1npa77ySx7CZPBeCmGoUzZxncsoOhrdvJ7D9Ew+oVtN5zN60bN1RdPKxWHP3bf0YNBFjwR79T03mlsBn+zF/S+M4/RvVYpluk+8Asuz6UBSgZFgP5MtMbop5CHi0h+d7BHgKayquXtLsuV14LJp3rZrxfU0rJ7gtp9nVneGhFFwmPp9u5skm2ZDCtIeI+QUpKxMXDqC0zUULe/K52LkX6ax+j6f0fqaqz1BXvSwh2vv4hFvzh79By9501ndst5e5eBjZvZXDzNtL79tOwcjmt99xNy6a7CLW7PzO5kbByeQa3P8XAE1sZ2v4UkZkzaNl0F60bN1w3F0+5r5+dr38rt3//GwRbq8vevhKZ73+O0OLVnqPOpG05z960RZ66uQ3kyihAi8uD2VEsIXjkQA8hn8YrF7fju0ax8XWhH4MtJI8dH6A7V+aNyzo9i/yoy8brYY3IDSHzw6gd8z0/hKUXnsLqOUP85W/zNM4tg1u2c/Tv/oW13/hiVW3f3CKFIHfoCAObtzHw5Fb03j5a7rqTlo0baF6/Dl9s8h1AXk+EaZF+bi8Dm7cx+OQWpC0c0d90F41rVl+TJC4pBC/87oeIzpvD/N/7rXF5jWqeA5HqBttGbZnhfoyQXEwXaIoGXdewGsUSgh8d7iNv2Lx+aQfRwPifgdWFfoSCYfH9Q72EfBqvXtzuuq/rKFJKujNFYkE/ybCHPq9SIC4eqciaB8h877OEltxKcOHKq19cIcf+4WNkDxxixSc+ij9RXWOTK2Hl8ww99QxD23YwtP1ptGiE1o130bJpA8kVy6dkLP/1QEpJ4eQpBp/cxsDmrRROnaFx7RpaNtxBy13rx8XFI22bo3/zT+RPnWbVp/8NLVj7szQY3dl+lKb3fQRF9RbZcsmq71yI4nd/f2XTpi9boqshgs/lWdyl15SSHWeGOdiX4/VLO2mPj8/nMkpd6IHTwwV+dmyAZe1x1s9u8mxVSykZzJcREtriIc+JG7Kcr8g3L8pFUl/4Gxrf8xeowfGLKpFCcOwfPsrQjp2s+Pd/ITrbe5OWsQjLInfoCENP7WJ45zPkDh6hYdXNzmHiXeuJzJpZozuv81IYQ8MM7djJ4NYdDD+1i2BHG813rKPptrU03LIKLVzdd8rK5dn/v/8MoRvc/K//OC5GwljS3/h/RG57JYFZizyPFelepFHynKiYKRrkdZPOhkhFPvcj/TkeOzHAHbOaWDUtOW5utRta6MuWzZaTQ5xJFXn5ojZmN1YWCZApGeTL3v/Y0jYda75jgafesKOUD+zEOHeUxKve5XlsJVz81iOc+LdPMfu976D9FfcT6uxwNc7M5sgdPkp6zz4ye58n88IBQp0dTvjj7WtpvGU1WsR9GGqdNrvbJgAAIABJREFU2iMsi+yBQww//QzDTz9D7tARYovm07BqBcnVK0kuX0qgpdmVEFm5PANPbuX0pz9H0+3rWPjhP7gmIbqlvVuwBnuI3/+Q57FSCET3EdTmGShh9wtSNUbeKMNFg58c7UdV4BWL2mj04BFwyw0p9EJKDvXl2Hp6iPnNUe6e20LQo6tmlLxuMlzQ6Uy6D6W8dB8DZ0Dze46bHyX9zX8jfMs9BOctq2h8JWQPH+X8l7/O4JPbCM/oInHzMkLtbfgScXyxGFYuhzE0jJFKUzp3nvyJk1iZ3C+JRsPKmwk0NV6ze67jHbtYIrP/IOm9z5N+bh+5Q4dBQnTBXKJzZhNobsLf1EggmcQ2DKxsFjOTJXfwMOl9+2lcs4quNz9I66a7rtk9i0KW1Jf/kcb3/DlqBYaTLKQRqR7nYNZDBJeUkp5MiaBPpSkarEjshZTsuZhh59lhVnUluXV6o2f38UtxQwm9lJLjQwW2nx4m5FO5e24zXcnKLcmiYTGQK3s+fAWnQqUYvog6bXFFYYHWQDfZH/wnje/+M88+yVrgHPLtIXfkOMbgEGY2i10o4IvH8Tc2EmhqIDy9i9iCeYSmdU650EenebuJtC4rX6v5UPyBKfh+JcbQMIUTJymeOTemWFsaNRjEn0jgS8SJzp1N8523X7cibdkffQH/zIWEl99R0Xi7/zSKP4Ta6K1AoC0kPZki0aCPRg9h1ZeTKZtsOz3E2VSJdTMbWTktga8G36UbQugNW3C4L8fe7gyK4jQGmNPkPvzxSoyKfHsi7DmtWdoWovuocwDrYZs4ltzj30SLNRBZ97KKxtd5cUQxj53qx84OYWeGEblhRCGHKOWRxTxCL4Flgs+P4vPxi4raEuyR7kWqhhIIoUZiqOEYSiSGFm9ETTSjJZvQGlpR440TIj9hKmGcP0Zhy/do+NU/rCjcWFqm82y2z0Hx2MrTEoKedJFYyE9DOFDV37Y/r7P9zBB9OZ0V05Lc3JGoqNzxKFNW6IWUdGfKHOrPcXQgz/RkmJXTEsxurE7gYcRdk9dpT4QJehV5KRH9p1H8wYpdNpe2qO/8Y9RwPdywGuxcGqv3rPMz2I011AuWidbUjpZsRk00oSWaUKMJ1EgMJRxHDYUdkX8RIZFSgm0h9RKilEcU84hiDpFLYWeGENlh7FQ/0jTQmtrxtUzD1zETX8cstMbWmudD3EhIKUl//WNE1r2c4NwXa2Z3lTkKaUSqe8SF4+35toSgN1Mi7NcqduOMpT+vs687w5GBPDOSYZZ1xJnd6N1NPGWEXkpJumzRky1zJlXk9HCRaEBjYWuM5R0JT9mtL4aUkmzZJFMy6Eh4d9fASJRNIYXauaDiB7qw/QdI2yJ294MVjb9RkVIissOYF044PxdPIm0bX/tM/B0z8bVNR2vuQI01XBNLW5QK2EO9WIMXsXrPYfaeReolfJ1zCEyfj3/6PLTWaXXh94h+bC+l57eTfNMHK/47isHzSGGhts72PIctJH3ZIn5NpSVW2QHt5RiWuGS09uZ0ZjaEmdMUYVoiREs0cNUgkEkn9D3ZEqYtKZq2I7pli1TJpC9XxqepdMSDzGwIM6856qmk8NUQUjKUd7rMtCfCnldUAFnKIQbPOlE2HuJ1f+k+Rqz5hrf9EVp8atdzqQXStjC7T2GcPoxx+iDSNEZE1BFSNdkyodwnopjDvHAS86KzGIlSkcDsJQTm3IR/5qJxDaOdKkghSH/ln4lueIDA7CUVzyF6T6BEkqgN3ju3CSkZyJWxhaQtEaqJn32UkmlzerjImVSRnlyZXNmiLRakORIgEfKRDPmJBpxmR35NIRbwEZlsRc2++Ow5/JpCyKeRHHlTyZCfjniwKh/WS2HagoFcCU1VaY2HKoqXdUoQH0dtm11RYtQo+ScfBp+f2IbXVjzHVEfaFub54+jH92GcOojW0Epgzk0E5tyE1jJtQgn71bCzwxinD2GcOYzVfRpf11yCC1YSmLsUNVgPSX0x9BMvUNz9GA0P/V7FOyJpmU7Z8ObpKBHvjUOklKRLBrmy6alcuVd0y6Y3p5MqmWTKJtmyRcGwMIXEtCXLO+Ksndk0uYT+Wr6mlJKCYTGU12kIB0iE/RWJhLRMRO9xlGQ7arzyGvlW/wUy3/ssjW//33Xf/GVIKbH6L6Afegb9+D60xjaC81cQmH/zlNn5CL2McfogxvF9mBdP4Z+5kNBNa/HPXHhdIq8mMlJKMt/+d4KL1xBefnvl8+hFRN9J1La5KKHKIomKhsVgrkw8XP0hbaVMOtfNtXpNWwgG8zqmLWiNhTwfuo4ibcvZAkYbUBvcJRhdcR4hyHzr44SW3UZo6bqK55lqCL2EfvhZygd3IU3dKQexZA1aYvJ3Y3ophF5y+hAc2o3IpwkuuZXQstum/Pv2gjXYTeY7/+EYRh6rWo5FFrOIwXOoHfNQApXtoixbMJh3XDkt8ZDrJuO1oi70lyGlJFc2SRUN4iE/DZGrH3S86Fy2heg7iRKKoTRW5zIo7tmMceogyTf+Rv1wDrCGeig/vwP9+D78sxYRWno7/ulzb8jPxhrqpXxwF/qRZ/F3ziG0Yj3+GQsnlYtqvCjs+CF2epD4q95V1echC2nE0AXU9rmua9f/jzmkJK9bDBd0pyFIOOipzHE11IV+BCklJdNmuKCjKQrNsWBFUTWX5rNNRO9JlEgCpaGzqi+ZNdRL5uFP0vCW30VLVt8ecbIipcS8cILSns3Yg92Elt1OaNltqNHxr6o5GZCmjn50L6XntwEK4dUbCS5chaLduG4daVmkv/Exwqs3EVqyprq5Lom99xj7sdhCMFzQKRk2DZEA8VBlLmEv3PBCPyrwmaKBLSVNkSDhgFbd6m+WEX2nUGJNKMn2KufSSX/z44RX3Elo2W0VzzOZkVJinjlM8ZlHkYbuCNiiW0aSlepcjpQS8+xRSnuexM4MEb5lE6Gb1t2wn5c1cJHMdz9D8k2/ha+xuh4GsphBDJ53kh0j1RkYuuUYlpYtaIg4wST1ombUVuhHt1HZkoEEkuFATT5oWc4j+s+gNHZWdfA6eo+5n/43ij9A7N633HBbcSkl5rljFHf+FGkZRNa+jMD85Teke6ZSzN6zFHc9ij3cR+TW+wguufWGtPDLB3ZS2ruF5K/8btUhqpee8YYO1ET1TVRKhkWmZGDYgkTITzwUqHmrwRtO6HXLJl82yesWAZ9KMhwg7K/Ogh9F5IaQqR7U1lkVlzYYS3H3YxgnD5B802+h+Ma/QcREwuq/QH7b95HFLJF1LyewYMV1EXgpJQjLKXlgj9S2ERYIAdJ2/h2LooKqgqo5ZRA0P2h+8Dn/Xq/F2uw5TfHpn2Ln0kTXv5rAvOU3nOGQf+Lb2PkMide8u+ooJWnqzq49HEdp6qrJZ6lbNtmSQdGwCAd8xIN+QjXSpikv9FJKDEtQNJzYUiElsaCfeMhfUdLTFV9D2MihC0ijiNo6p6KSw5dTPvQMxWd+TvJNH0SLeY/hnazY+QzFp3+McfYo0dteQfCmW69Z6KAUAowS0ig6/5plMHXnP/oCjlBrftA0UBwhR1Gcn19M4oi/sEHYSNscWSQM53e+oNP8PRB2DvUCYRTt2rlUjHNHKWz7PkooSmzDa2veZ3giI22L7Pc/h5ZsIrrpTdXv3m0LMXgORjNoPbQifClsIcjrFvmyiS0lkZGEp5BfqzgwZMoJvZQSwxaUTRvdtCmbNqqqjHxYGkFfbVbIS6+nFxGDZ1ECEZTm6TURJeP0IXKPf5PkG3+zap/iZEHaNqW9WyjteZLQ0tsIr7l33LNApRCgF5DlPLKUA7MM/iBKIALBsCPI/lDNhFgKG0zdWUCMElJ3FhR8fpRQ3EmkC8XGXfilsNEPPUNh588IzLmJ6PrXoIYqiySZbAijTObhTxGYs4Toba+oej4pJTI7gMz0O4lV0drmbBiWTdGwKBo2hm0T8mmE/I6OBT0I/6QTesOykXIkQUYIbCGxhSPupi2wbIFPUwmNfBAhv1Yzy30sUgpkph+ZHURpmoYaq038sn5yP/knvk3igV/D33FjdFoye8+Rf+KbqJEEsU1vHNfIImlbyFIWWcxAKQeB0C9ENhi95uWFpZSO6JfzyHIOygXHyo82oESSNbMSr4TQSxR3/hT9+PPE7nodgQUrbwh3jijmyHznUwTmLSdy2ytq8p6lXkAMnEUJRh1Xzjgs1rZwDNiy5RixhiXQVAW/phLwqWiqik9V0FQFVVFQFAVFAVVR0FR1cgn92aEcCqCqCpqi4FNV58361JHaDmrF2xu3SL2AGDwPPr/TkaZGD6N+bC/5rd8j+dpfw9fmvlHxZEVaJoWnf4J+dA/RDa91QgHH4W8npYBiFpEfhnLesZqjDSjhxDV1m7hBCgHlHLKYcRYjX9CJ3oo2jNu9mj1nyT/+TdREI7F73nxDuApFMU/mu/9BYOYiIutfUxuxFzYy1YMsplEau5y/2ThqkZROiQPTth0jd8TotYVAjBjDUkIi7KcxGppcQn+tX3Ms0jaRqV5kKVPTP6SUktLeLZT3biXxuvfha5lWg7ud2FiD3eR++mW05g5iG98wLiUdpKkjc4PIfMqx3GNNjpU8ScoFSCmhlEPmh5GlrHPv8ZaKU/Ff8rVsi+Luxynvf4rYPW8iOG95zV9joiHKRbLf/0+0ZBOxex+qWfjpJUNQ86E2dVWcTVtLJp3r5noIvRS244fLDvwiNr6GftvClkcwu8+QeO2vocWndos9KSXlF7ZT3PVzx4pffEttz0ykBL2AyA5AOY8Sa0aJN1dcLXSiIG3LEfzcoNPFKtGKEqm9xWj2nCb3s68SmLWI6IbXTfloL2mZ5B79KqKYI/Hq96CGa7OISikdIyPdN5I02TGubrirURf6l0AKG5kbQmb7nTIGDZ01FQxRzJH76ZdB1Yi/8p1TvgStNHVyj30TOz1I4pXvQGuoPgb5l+Yv5RDpXrBNlEQbSqxx0ljvbpFSQjHjLGS26QhItLadqoReckIRU/0kHnjvDWB8CIpP/Rj9+AskXvXOmkYiSWEjM33I3JBjJCZar4vg14X+Ckjbclbj7CCEoqjJ9orrW7wY5sVT5H76ZYI33Upk3cunXI/Ry7FzKbI/+Dy+lk5i97y5ppaiLBcQ6R6wjHERvonKLxY2a+R9187Cl1JS3ruV4p4nSbzynfi75tZk3omMfmwv+c2PEL3jVQSXrqvtTtMyHK9AfthxwSXbr+kusy70I1yKfsgNIouZkT9GmxNiV8vXETal556ktG8b8fsfqrgxwmTC7DtH9gefJ7x6I+FVd9dOjCwDmepGlguO0MWabgiBH4uUEsp5RKobUJwQvxoaJcbZI+Qe/RrRO19DaMmtNZt3omIN95H78ZfwtU4juvENNa/5L23LEfzcIASjTvZ8OFGvdfNLLzgetW4sE1lIIQspELbjz401OYkxNcZK9ZN/9GtOSYP7H5ryW2IA4+xRco9+ldi9v1JxD8/LcWKX+5GZfudwMtk25Vw0XpFSOj78VI9jpDR21uwcyRruI/u9zxK6eT2RWzbVZM6JjDR1Ctt/iHH6ELF7f4XArEW1fw0hkMW0I/iW+YvIqnE6uL0hhV6aOrKUQxbTYJScMLtYI4Ti4xPeJ2zK+7ZTfPYxIuteTujmO26Iei36sX3ktzxC4tXvxj9tTk3mlHoRMXQeVJ9jvY7z9lcIiWHbmLbEsgXmSO6GkBIhJOKyr6M6Erd8KfxXc0KAfSOxzrVsKXclpG0h073IYhq1qXYJPHYuTfZ7nyUwe3HNwhEnOsa5o+Qf/xaBWU4I5nh19JJGyVmkC2mnbMZI6C+BcM0+5xtC6KVt/XIGpG05NSoiSWfbNI4Pn9l9mvzm76CGIk6Mco0PICcq+okXyG/+DsnX/3pNwkWllCMJav1Obf9xcNOMxiWXTcvJrLZsbCEJjORojAq2NiLiquokpIy9CyG5tAjY0lkcLFtiCoFh2SiKQkBTCfk1Qn4fQZ86PsZFOY8YPFfTBB5RLpJ55NMEZi4gcserbwixF3qJ4o4fYZw+SGT9awguWj1u73s0YkwW0shSFqR0amaFYk4wSBWHuFNK6KWUYFtglpFGaaRuSQksw8l6DEWdDy4QGfcvqSjmKOz4Iea5406T4hsk6xDAOHOY3M+/TvJ1769JBIO0DMTAWVAUpzxsDaMWRstUF3SLkmkBEB4jwn6tdkLsZHNLDMspzVEybWwhCPl9REfqmdSyEYWTwNONLOWcQntV1FAfRZQKZL7zSYLzVxBZ97Ia3OXkwOw9S2Hzd8AXILbxwWuS6yLNsuN5KOedjGlFgWAEJRB2XDz+EPjctSYcd6FXFKUJ+BxwPzAI/ImU8mtXuO5dwG8DC4As8FXgT6WU9phrpJ0ddApHSeGI+qXCUYbzo6hOfZJA2Nn6jP57jURWGGVKe7ZQfmE7oZvWEl57P2oNipxNFqz+C2S++xmnhEPnrKrnk+U8YuDMiC++utr+Y9FNm1zZpGBY+DWFaNBPJODDpyrXdEG2haBo2BR0k7JlE/b7iIf8NauoCr9omKE0dqDGq99RimKO9Lc+TuTW+wjdtLYGdzg5kEJQPriT4s6fEZi9hMhtL79m52xSSrCMS/WRpFkCo+xooM/vCL7mdwrtab4xBfdUlEAYNRgZd6EfFfVfA1YBPwLukFIeuuy6DwD7gV1AG/B94FtSyn8Yc420B846Yq6ol96Qovmc6oK+wHU7lJOW5XwJdj9GYMZC50twg3WDEoUs6W/8q5MItWBF9fNlB5Dpvpo0eQDHpVLQLbJlAyEk8ZCfaLB2VUyrxRaSomGSK5vYI/cXD/nRauBalGYZ0X/aceU0T6/6jMga7iPz8CdJvOpdN0To5ViEXqK0ZzPl/U8RWnKrU4CvRolWXpFSONVRLd1xUY8YvwgbpyiYQIkkUWON4yf0iqJEgWFgqZTyxMjvvgh0Syn/5Cpjfx/YJKV87ZjfXdcSCFdCWiblg7soPfckWnMH0Tteja916pcwuBxp22Qe/oRj6ay9v7q5pBxxOWRR2+ZWfeAqRvoAZ0oGAU0lUcMeBOOFU5vcpGiYxIJO7+JqBV8K23GBSYHaNqdqo8g4e5Tcz79Gw0O/f0PUx7kcUchSfOZR9OPPE1q6jvCqu6tqQj6ejKvrRlGUVcB2KWV0zO/+ANg4VsBfZOx3gUNSyj8d87sJI/RCL1E+8DTlfdvwtc0gvPY+/O03RrXJK1HY/gOs4T4SD7y3KmtRSokcPIe0DEeMqjhEHG30ni4ZBH0aDZEAwSr6AF8PLFuQKRnkdZN4yE8yHKyq+5CU8he9E9rnVX1IW9z9GMbZoyTf8IEbNsTVzqUoPfck+tE9BBevIbxyw4TbzY+30G8Aviml7Bzzu/cDb5NSvmhArqIo7wU+AqyUUg6P+f11F3o7PUDp+e3oR54jMHsJ4dWbbkgLfizGmSPkn/gWDW/9g6q2sFIKRP8ZAKeRQxUWbMmwGCroaKpCUzQ46QT+cixbkC4aFAyLxmiAeLDyblVSSicEs5BG7ZhX1eG2lILs9z6Lr2NWTeq7T2ZEIesUJzz0DP6u+YRXbcDXOWdC7ByrEXo3pkAeuNy5mgRyL3FDrwf+Frh3rMiP8pGPfOTS/964cSMbN250cRvVIW0L49RBygeexhroJrR0HQ1v+yO0eG2bDExGhFEm/+S3id33lipFXjoiryiOyFf4cNhCMFTQKZs2zdEgkcD4NVy+lvg0lZZ4iLhlM5Qvky+btMRCBCpYwBRFQWnsRKgqovckauf8ihMEFUUldt9DpL/2UYLzV+Br6bz6oCmKGk0QvfMBwmvvRz+8m9xj30DR/ISW3UZw8S3jFod/JTZv3szmzZtrMlelPvr/Bs6PdcmMuf4VwJeAV0kpn73Cf79mFr2UEnvgIuWje9CP7sHX2EZo2W1Or80pXtHPC/kt30WaZeL3PVTxHI675ixSCNS22RW7fgq6xVC+TCzkoyESHPe+BNcLKSU53SRVMEiG/STD7kLsroS4ZNnPr8qNUz6wk/LBXSTf/NtTvm6TW6QUmBdOUj6wE/PsEQJzlhJcfAv+GfOvuZvrWoRXfg2QwPuA1cAPgdullIcvu+4e4FvA66SU219krnEVeikl9nAfxsn96Mf2Ii2T4KLVhBavQWtsHbfXnaxYQ71kvvMpGt/+oaqseTF8EamP+IwrEAkhJamCTtGwaI2HCPknVjOR8cK0BQO5MooCrfFQRVm3lw6+9aLjxqlwkZVSkvn2vxNauu6GCrl0iyjm0Y85RqOdSxNcuJLgvJvxdVbnonTLtRD6RuDz/CKO/o+llF9XFGUmcBBYIqW8oCjKE8CdgD5m+FYp5avHzFX7Wje2jdV7BuPMYYyTB5CWQWDuMoILVzl/hClqFdaCzHc/Q2D2YsIr76p4DpEdRGYHUDsXVGRRWragL1fCp6q0xEJVHVS+6D1KSaZkMlg0GCwYZMsWRdOmOJI9O/YbGdBUIn6NsF8jHvTRHAnQEg3QFAngG4d7k1KSLhrkdJO2Chc5KaWTq6CoKC0zK/7Om73nyP3ov2h4x4dvqNwRr1ipfvSjezFO7UcUcgTmLiUw+yb8M+aP2+c2pTJj3SCFwB7qwew+hXn+OOaFk2gNLfhnLSYwdym+thl1cXeBceEE+ce/RePbP4SiVbYNleU8ov+MI/IVhFDqlk1ftkQyFCARrvxw8n/cl5T0FwzOpYqcTZe4mCkR9muXRDsZ8hPxa0T8GkG/ijpSBEEChu0kQBVNm5xuMlQ0GSwYZMombbEgsxrCzGwM05UI13RRKhoWA7kyzdEgsZB316IUAtF7HCXaiJqsvCF97mdfRmvqIHLrfRXPcSNhpwfRTx3APHsEq/ccWtt0AjMX4p82B1/7zJq5iae00EshENkhrP6LWAMXsQYuYPWeQ40m8E2bg79rHoGZCyds7OtEJv3wJwnddGvFpWulbSK6jzk9dytIhhoVtpZYkGiwNg/DQEHncF+eIwM5FEVhdmOYmQ0RZjSEifir86matuBipsy5tLN4ZEomC1pjLGmLMT0Zrsl5gjGy8MVCfhoq8NtLU0f0HHfOSUKVtXa0Uv1kvv0JGt/5J1O+kU6tkaaOefEUxvnjWN2nsYZ78TV34mufga+1C19rF1pje0UtDyet0EspkIaO1EvIcgE7n0HkM4hcGjsziJ0awE4PoEbi+FqnOR9S63T8HbNQI7XvT3ojYXafJvfo12h854crOlSSUiL6TqEEI6iN3qM08rrJcF6nPREmWKUACyk5PljgmfMpCobN4tYYS9rjtEUrP+B0Q7ZscmQgz+H+HGVTcMv0Bm7uTBCoMkvXEoK+TImQX6MpGvQu9sUsYug86rRFFR/O5n72ZbSWaURuuaei8XUcpKlj9p7HGriAPXABq78bOzuEGmtAa2xFa2hFizegxkZ+wlGUYBglGPofz+WkE/rB//gzpLDBslB8fpRQBCUYRo0l0WINzr/JZrTGNrSGVpTA5O4VOhHJ/uS/8XfOqtg3L7KDyPyw47LxKESjIt+RDFcUWjiKLST7e7PsPp8mEtBYO6OB+c3R6+K268mW2X0hzbl0kRWdSdZMbyBcxQJmC0lvplix2IuhCyBs1NbKahWZfefJ/fiLNL7rT+sRODVG2hZ2Zgg71Y+dHnSM23za+SkVkXoRaeigaY7Yaz7Cq+4meuu9k0vo7VLBeQM+35TLxBOGSfHMWYrnL1A6f4HSxR6EriNNC2FZBJoaiC1aSHzRAqLz56IFr/0iJgpZUl/+Rxrf/WcVxQU77oFjI355b1v7gm4yVAORPzlU4MmTgyRDfm6f1cj05LWLb34pUiWDZ86nOTFY4LaZjazqSlbs0hkV+3DAR1PU2/dECoHoPora2FlxPfv0N/+N8Jp7CM5dVtH4apC2TfHseXJHj5E/epxydw9oGqrPh+L3E2pvIzxjOuEZXUTnzsYXvT51asaL0fo3UowUftT8aKHw5BL6650ZW0vK3b2knt1D5vn9ZA8cIn/yFKHODiIzpjtfxK5OtHAYxedD8fswBgbJHT3ufHl7+5n17l9l5jveiha5dkJV3PMk9nA/8fve4nmskxTlFNZSG9o9jS2bFn3ZMh3JcMVZrpmyyePHBxgumdw7v4U5TRPzAR8sGDx+YoCiaXP/gtaKFyJbCHoypZHSCd6yX2Uphxg8h9q1uCKDqnxwF8aZwyRe/W7PYytFCkHvj37KyY9/GkWB2OKFxBctJDy9y+noZFkIw6Dc20fp/EVK5y9QPHOOUGcHiWU3kbh5KY1rVhGdN3fK7UQmnetmMgu9mc4w9PQuhnbsJL37OaxiicY1q0muvJnkspuIL1nkWrSLZ89z8uOfIv3cPub9zm/Q+frx7/ojpST91X8mdvcb8E+f5318IY1I9zj+Xw/x2qYt6EkXaYmHiAQq8xsf6M2y+dQga6Y3sGZ647iEOtYSKSXHBgs8fmKApe1x7pzdXFGUTjWfnRg4C5oftcl7iQ+hl0j91/+l8V1/ghoe/zOx1HN7Ofo3/4QWCjH/Dz5I45rVrsYJ06Jw4iTZA4fIvHCA1LN7sbJZGtaspvmOdTTfeTvhrslf4qQu9OOIlJLckWMMbt7G0LanyJ84ReOaVTSvv53GdWuIzqu+Dkb2wCEO/ulH6HjNK5nz6++p0Z1fGWuwh+wPPkfju//Uc2KNlBJx8bATZRN2H+UkpKQnXSRWgVUKTrjjY8cH6M2Vec2SDtpik+vMpmjY/ORoHyXT5oGbOkhWEDo5uhua1hDxVJJZWiai+whq58KKwl+zP/lv/NPnE15+u+exXhh6ahcHPvwXLP7zD9P2snuqfqbKvX2kdj/H0FO7GN6xE18yQcudd9By93oaVq9CDUy+zPi60NcYu1wmtetZBp7YwuDWHWjhMM13rafl7vU03rIKNVC77kij6P0DPPPWd7Poj/+QtvvHL9KhsPO/E4muAAAYoUlEQVSnYBpEN7xk4dErIrKDyGIGrcPbTmAwV0ZISWs85PkBzpRNvrO/h/Z4kPsWtFYd0XK9kFLy7IU0z5xP88CSdmY2RjzPkSkZ5MsmnQ0RT35/keoBy6joYFY/8QLl/U+RfPADnse6pXD6DM+963+x/KN/59qK94IUgtzhowxu2c7g1h0Uz5yl6fZ1tG66i+a77iDQMDnqXdWFvgYYwykGt2xj4MltDO/aTXzRQlrvuYuWjRuIzq6+y5IbsgcPs/cDv8ttj3yNYMv4lEhNfeWfiN3zZvydsz2Nk0I41nzbHJSge5Eq6CbDBZ2uhqjnFnsDBZ2H9/dw6/QGbpk+OR7Gq3EuVeQHh/u4b0Eri1q9uUOklPTnyvhUheaY+0NwKWzEhcNOLRyPWZvSMhn+7F/R+J4/Rw15X5yuOr9ts/tt72Xagw8w/aE31Xz+K6EPDjG0bQcDT2xleNezxJcspHXTXbRuupvIrBnX5B4qoS70FSClpHjqDAObtzHw5Fbyx0/QfPs6WjbdRcvd66/bKn/8Xz6OPjDAsr//65rPbedSpL/2UZre9388H1SJ7CCylEVrd9+JyBaCC6kiHRXEyl/MlPjuwV7umd/CkraplQzXl9d5eH8362c3saLTW7MPW0gupgu0xkOEPZRKEOk+MMsVWfWZ7/8nocVrCC5c6Xns1bjw9W/T++NHueWLn74uYbF2uczwzt0MjuiAP5GgZdMGWjfeRXLFsoozxseDutC7RBgmqef2MLhlB4ObtyFMk9a776Rl0wYa1665LqGOl2MXSzz1wJu5+aN/R3LF8prOXT6wE+PCcRKveIencZd88y2zUELuo1z6syV8muo5NLA7W+aRAz28clEbc5snZlRNtaSKBt/a383aGY2snOZN7Iu6xVChTFdj1LULx7HqDzmH6B5r15ee3441cKGq6qZXwsrl2fHKB7nlvz5FbMH8ms5dCVIIsgcOM/DkVgY3b0MfGKBlw3paNt5J8x234Ytf3yTNutC/BKWL3Qw/tYvB7U+T2rWbyJzZtNy1ntZNdxFb5D3Z51pw/ivfJPXsHm7+2N/XdN7cz76Cv2seof+/vTOPjqu67/jnvvdm1YxGu6zFMljejbEBY1CAkEASaEvIQhYoTSFpS5M0pwk9abM1TQKBLCU9aZqQNicrkNAsJzQJCUkTwClb7BiDDbawBbaxFmuXZtHs793+MTIoirDulUaakXifc+YPje59c+c3733ffb/7+/3uGedr9ZPJKM74AGbzOuU+qWye4YSeGAGMJrPc/WTvgon8cDzD40dHOdwfo3csRd9YiqF4mqmnZHXQS3N1gKbqAKvrQ5xzeg1ttcGinytjqRx3P9nDa9fWs7ZOT0QGYim8lkF1UP0m6oz2AkI7Aic/0k/sZ9+g5vqPafWbjeN3fI/oUwfZ8q+fLupxi0Wq7wTDDz7E8P89zPjefVRu3kjtKy+g9hXnEVq3ZtHDN12hn0IuFmfs948z+thuRh/dRT6RoOb8c6m5oIO6Czvw1tYs2GcXi1w0xsOvu5KL7r8XK1S8WcToN28m8qZ3a5drtvufRYRqMEJqtpNS0juepDro1aphk8za3PVENx1tNWxpmv9G4ifp6o/zP49381jXMMPxDGefVsOmlggtNQFaqoPUh1/c2k8Co4ksfeNJToylONwfZ8/RUWxHcl57LVec1cKO1bXa6w0vRX88zY+e6uPNZzTTXKnuP8/ZDn3jSVqqgliKC9QvJLq1btYSKSklo1//JFVXfwAzXK3cbzZ2v+0vab/x76jtOK9ox1wo7GSK0V2/Z+Thxxh9bHdBVzp2UHP+DmrOPxd/04oFH8NC7zBV1mRHRhl/Yl/htecJJo4cI7LtTGrOP5czvnAr4fVrl1zihCdSSdXWLYw8upvG1xUnAsdORAt7uFbVafWT+SxkU1rZlYlMDtMQWjHftiP5WWc/G+pDRRH5nO3wv0+d4Ee7u+kdTfKm7Su55a1bWddUOWsse1NVgM2tL7pTpJT0jCZ55PAw/3bfM2RyNlftaOON57RSGZhfmN6KsJ/L1zXy04P9/MXZrYQUbeYxDcJ+D2PJDPVhtbwN4fGBN4hMRhEhdcEWQuBZ0VaozFgkoU8PDJLq6aP63HOKcryFxgwGJhdsCyVDUj29jDy6i5GHH6XrC1/CE6ks5NOctZWqs7cRWNlSVt6CJTWjz0VjJA53EXv6YOF1oJPceJTI1i1Unb2NqrO3Etm6ZUHCHxeb7u/+gNjBTjbf8omiHC/z3FOkn/4dkTf8jVY/Z7wf7DxGbataeynpGZugIRzAr7EAu/O5YYYmsly1pWleVSCllOzsHOSLv3yGhko/13Ss4qINDVqx57Mdf3/3OD/cdZxHDg/xrovbubpj1byP/8ixUZ4fS3L1thbl7+84ku6xCZo0ykk4iTFkYlQ7RDa5+9fIbJqKC1+v1e+l6P3hPYzu2sOW224pyvFKiXQcEoe6GNv7JNG9TzK+dx/Stglv3kjl5o1EtmwmtGEdvob6eYn/sprR26k0mcEhUr19pI53kzzeTfLYceKHusjH4oTWtVO5eRN1F1/E6vfeQPC0trJaGS8WNRecx/PfurNox8sP9WI1qIn1VOTEGEZtm3L7RDqH1zS0RL4nmqJzMM7129vmJfLHRyb43M8OcmI8xYdfv4mOtcXfUUwIwda2ara2VXNkMMEXftHJPXu6+eiVm9m+eu4hsa9YVU1PNMWennF2rFSbNRuGIBLwEE1l1Wf1wQhypBtp57UqW1oNraT27lRuPxujux+n5hXl77JRQRgG4Y3rCW9cD9e+HSklmRMDxA52EjvQyfE77yZ+qAtsh9C6NVS0n06gbSXBtkKtHl9DA1Y4tKBPACUR+s6bPluoWZFOk4snyMfi5GNxMsPDOOkM3vo6As1NBFetJNC2kqpzziK0bg2BluYl54aZK8FVbdiZDOm+fvzN8/f/2cN9+NbrPSbLbAocBxTj5qWUk6Kj52v+5aFBXrO2fl7VHu/b18fn7z3I9a9czZ93nIbHWvjzZHVDiC9ft50HDw7wsR/u44qzWnjPpWuVfeZTEUJw2boG7trbTXttBbVBtafSsN9Lz1iCvO0ofa4wDESgsuC+CavfmMy6ZvLDfUgp5y1IUkrG9z5B+/tumNdxyhUhBP7mFfibV9Dwmle/8H5maJjEoS4mjj1P6ngPo4/tItXdQ2ZoBOnY+Orq8FRXYYVCeCpDmMEgwrIwPB5qL5xfZnJJhD60th3DsjD8PqxwGE84jBUJ46urw4pUlpVvq1QIIYhs3UJ0/1NFEfr8cD/BC/TqxstkFBGMKP8eqayNYQitgmW7jo/REPJpR52cxHYkX/rVIR48OMB/vnMH65uLt4irghCCSzavYNuqaj7yg328/87H+ezbtxGeg+++KuChY1UNv+ka4m1nNivZ3TQEIZ+HWDqnHsZaEUEmRkFD6I2Kgl1lMo6omJ+NM4NDOJksgbbyTU5aCHz1dfjq62YU7fzEBJmhYfLRGLlYnHw8gZ1MFibEudy8gzJKIvQrr3lrKT52yVG5aQPxzkM0Xv7aeR1H5nM4E1HMiJ5rQaZiGFXqN4dYOkulX32zj/FUjif7oly3Xd01NJV0zuZD//0kyUyeO97TQZXiLHghqAn5+Mp127ntF89w3X89xpevO5fmav2KlWe1RNjfH+Pw8IRy5mzY7+VEtBDlpGJ74Q8jh7uRjqP8hCyEwKxuID86iHeeQh/vPER44wZ3QjcFq6JiQUstvzz8IEuU8IZ1Bd/ePLHHhjAra7VK1Uo7D9k0KCZI5W2HTN6mwqc+d/jtZCXKsEafk+Rshw9+7wmCXpPb33luSUX+JJZp8OHXb+Kqc1fyt9/cxXA8o30MQwguXVPHzueGsR21oAWvZeC1DJLZvFJ7YVrgDUA6oTU2s6YRe2xQq89MxJ85THiDek6Gy/xxhb6MqWg/neTRY/M+jh0dxqzWC6sknQBfhXKFy0QmR9DrUV5MHZrI0BNNz6mGjZSSm+95GgHc9JYzixZRUyyuveB0rtjWwt/fsYeJjJr4TqWtKkhN0MOBgZhyn5DPQ0Ljs0QgjEzHtcZlVtVjR4e1+sxE8ugxKlafNu/juKhTXleIyx/gb2kmMzSCnU7P6zj2+DBmRDN+Pp3Q2lx6IpMnpDEz33V8jO2tVXMS6a898CxHBhN8/pptZSfyJ7nhkjVsbI7wT3c/oTwzn0rHqhp+d3wMRzEUucJrkcrllT9L+ENI3Rl9VR3O+JBWn5mYOPo8wdMXp1CgS4HyvEpcADAsC/+KRtJ9/fM6jhMbxajUywiWmaRyXZuc7ZB3pHJIZSKT58hokm1zWDh9tGuIH+/p5ovvOIfAHDcwWQyEEHzkyk3kbIevPfCsdv/WSICgx+TISFKpvWEI/JZJKqc4q/cGIZcubFWniFlZgx0bU27/UqS6ewm+zBZiS40r9GWOv6WJVG/vvI5hx8cwNDIapeNALlUQAwWS2TxBr6m8uLbvRIwN9SHt7QTjqRyf+vFT3PyWrdSFS1+AbjYs0+CWt27lR7uPc6Anqt3/rJYIe/vGldsHfRZJRfeNMAzwBCCrdiMBMMLVOPH5CX0+kUDmcniql0fZ6aWCK/Rljn9FI+kTA/M6hpOIYoY1LqxcGiyfckRGKptXnl1LKTkwENMuzwvw1fu7uGh9AzvaF6ZW/0JQX+nn/Zev5zM/PYCj6cJZXx9iIJ4hls4ptQ96LFI5G9XMc+ELFHIlFBG+QGFfguzcXYnp/gF8TY1uxM0i4wp9meNrqCczNL8FMGci+kIctAoym0J41UIDpZRk8rZyslNvLI1lGDSE9KJknhuIc9++Pt772rVa/cqBK7a1YBhw75N6T2aWYbCuLkTnoJov3TINDFHYelEJbwB0hF4IjIowckJvEXcqmcFh/A3Fz1h2OTWu0Jc5vvo6svMQemnnkdk0IqARo5tNFURApantYBoGpuLs/9BQgo0N+uneX/l1F++6uF27tn05YBiCf/yzTdz+my6yeVur74aGEIeH1RdNAx6LdE7tM4QngNScnRsVlTgT6tFA08kMDeNdoN3TXF4aV+jLHE91NdmxuftFndQEwq8eJgkg8xnljaQzOVvZ1y6l5LmRCdo168x39cfZ3z3GW3bMLbGqHNiysor2hhD3PtGn1a81EmAslVMOnfR5DDKqNxOPr7Agq1Fk0AiEcFJ60TpTyY2N4a0p/1Lhyw1X6Mscb00VuVH1BbnpyPQEhsauUADkMmApCn3exqdYV2YslcORUF+h57a54+GjXHvBaQS8S7t43V+9qp1vP3RES1hNQ3BadZCjo2qLpj7LJJtXc90I0wIhwFGPvzcCFTipCeX208mNjbsLsSXAFfoyx6qsJBefu0/USScRGps6SykhnwPF7eaytqNcIrcnmmJlJKDltkll8+zsHOAN5+hX3iw3zlpVjWUI9h3Xu3GvrArQE1XzpXtMg7ztKMffY3khn1Uei/AFkBn1SJ3p5GJxPJHFrUfk4gp92eMJh8nH5i70MpPC8GnUXLHzYJhKETdSSnJ5B69i0lJvLE1LRL2yJcBvnxnkzJVVS9I3Px0hBH+6tZlf7j+h1a+l0k9vTM2XLoTAMg1yqguylrewuYwiwhdEZtQXcKeTj8exwstrs/elgCv0ZY4ZqsBOzn0GJbMZhFdDXO0cWGqVF+3JkrWq2+oNJjI0hvQE++FDQ7xqY6NWn3Lm4o2NPHpYL7u0rsJLPJNXjqY5OatXQZiews1dEeH1I7P6NXxOkk9MYIWW54bv5Ywr9GWOGQyQn0hq+XWnInMZhFdDXO0cmGpCn7cdPKbibkhSMprMUafhn5dSsuvZETrWatbpKWPWNIZIZW26R9T93IYQ1AS9DE+ozbwtQ6jP6E2r4KpTRHh9yNzc4+jtZAozoPdU5zJ/XKEvcwzLQhgGMqd+MU5F5rIIj4a42nnlKpd5RyqHVUbTeYIeU6s2Te9YCsOA1hr1NYZyRwjB2adXs79bz09fG/QwllIUetNQr69jWlqLscLjRebUXT3TsdNpDL8r9IvNrFedEKJGCHGPECIhhDgmhLjmFG1vFEKcEEJEhRDfEEKUvnbsMsDwenGyc7y48lllVwwAjg2KQm87EkvRbRNN54j49Tbj6OyLsqFZP4O23FnfVElnn14sesTvIZpSE2TTEOpCb5hIRz22X5gepMYTwHScTAbTt/TXW5YaKtOrrwBpoAG4FviqEGLT9EZCiMuADwGXAKuA1cCnijfUly+G14OTneOMPq+3N6iu0Kv65xOZPGG/XhGyI4MJ1jYuv4W7tSvCHBnQi0UP+yziirH0phDYqmUQDLPwm6tiWci8funlkzjZHMKrv/uWy/w4pdALISqANwMfl1ImpZSPAD8B3jFD8+uAr0spO6WU48BNwPVFHu+yYufOnUrthGUhbb2MyhdwbNDZPF1KUHTHSCmV688nczbBU5RJmMkW/eNpmqqW32N+U1WA/lOES85ki4DHJKWYCGUYQr2ujjAKv7kiwtS8MUxD2jaGpX7DV71GXE7NbFf0OiAvpZxaZ3UfsHmGtpsm/3eS/UCjEEK9bOLLDHWhN5Gq5WenIR0HIXSE3ilc/Ao4GkKfyTv4T5FYNZMtBmNpGjTDMZcCjZV+Bk8RLjmj0FuGcmkDQwj1OHphFH5zVXSfAKahswYErtAXi9mu6BAw3ZkYB2Z6ng4BU2uxnuy3/J69FxkhDCRzi7pBOqDoXim0l4BaeylVWxYWblX9+SdJZvW2JlwqBH0Wyax6lUko+N3zGtUvlVsKoTejF0Kn+R/jSCjTzWKWM7NZPAFMT2OLUBD72dqeXEWbe7aPCwChdWsKj8xzwAhVYQQ0dpC3PMo+fcs0MBXFu8Jrau1ABdBcFSASWH7+XNMQnNEaIW+rK6bPMqlStIUhUE5iQxiFmjeqWF6s6rlXn6xY047hWX6/abkjTjWrmPTRjwKbT7pvhBB3At1Syo9Oa/td4KiU8p8n/74UuEtK2TSt3XzmAy4uLi4vW6SUcyrkf0qhBxBC3E3hSfCvgbOBe4EOKWXntHaXAd+mEHXTD9wDPDr9huDi4uLisrioPN+9FwgAg8BdwLullJ1CiDYhRFwI0QogpfwV8HngQeAY8BzwiQUZtYuLi4uLMrPO6F1cXFxcljZFX/52M2lfRNUWQojrhBB7Ju3QLYT4nNCKiSx/dM6LKX3uF0I4QmfXlCWA5jWyWghxrxAiJoQYEkJ8bjHHutBo2uLjk9fHuBDiwZkSN5cqQoj3TWpAWgjxrVnaauvmQlxAbibtiyjZgoJr7P1ALXAecCnwwcUa5CKhagsAhBDXAhYakYJLCNVrxAv8GvgN0Ai0UHCfLidUbXEl8G7gIqAGeAy4cxHHudD0AjcD3zxVoznrppSyaC+gAsgAa6a89x3gMzO0/R7w6Sl/vxo4UczxlPKlY4sZ+t4I/LTU36FUtqAQmnuIwk3PAYxSf4dS2AK4AfhtqcdcJrb4CPD9KX9vBlKl/g4LYJObgW+d4v9z0s1iz+jdTNoX0bHFdC4Gnl6QUZUGXVvcCtwODCz0wEqAji3OB54XQvxi0m3zoBDijEUZ5eKgY4v7gQ4hxFohhIdCyZX7FmGMi81s4ZNz0s1iC72bSfsiOrZ4ASHEuyiEsd62QOMqBcq2EEJsBzqA/1iEcZUCnfOiFbga+HegCfg58JNJoVsOKNtCSrmbwmz/EJAErgL+YaEHWAJmc1XOSTeLLfRuJu2L6NgCACHEGynMZv9ESjm6gGNbbJRsMbnoejvwASn/oADLnJJEyhSd8yIJPCSl/JWUMi+lvI3COs6GBR7jYqFsCyHE+yisXbUCPgpFEx8QQmjsk7kkmO1cn5NuFlvoDwOWEGLNlPe2MrMb4gCwbVq7ASnlWJHHVCp0bIEQ4nLga8AVUsoDizC+xUTVFpXAOcD3hRAngN2T7/cIIS5Y+GEuCjrnxf6pfwidXdWXBjq2uBy4W0rZJ6V0pJTfAaqBjYswzsVkthn93HRzARYT7qawYBAELgTGgY0ztLsMOEHhh6oGdgK3lnoxpES2uAQYAS4s9ZjLwBYNU17bKSzGNgGeUn+HEthiHTBBYSZrUlik7wKsUn+HEtjiVuChyfPCoFAqPQ5Ulvo7FMkOJuAHPgPcQeGpxZyh3Zx0cyEGXE2h/EGCQobs1ZPvt03+MK1T2t5IoVxCFPjGcrqYdWwBPABkJ987+fp5qcdfqvNiSp/TAJtlFHWjawvgTZPiHp08T/5IBJfyS+MaCQJfn6IXe4DXlXr8RbTDJylMaqa+/qVYuulmxrq4uLgsc5ZVxqGLi4uLyx/jCr2Li4vLMscVehcXF5dljiv0Li4uLsscV+hdXFxcljmu0Lu4uLgsc1yhd3FxcVnmuELv4uLissxxhd7FxcVlmfP/VfO57190P9oAAAAASUVORK5CYII=" alt="" />
matplotlib也可以画3D图,这里暂且略过。
转载于:http://whuhan2013.github.io/blog/2016/09/16/python-matplotlib-learn/
python数据分析之matplotlib学习的更多相关文章
- python数据分析工具 | matplotlib
不论是数据挖掘还是数学建模,都免不了数据可视化的问题.对于 Python 来说,matplotlib 是最著名的绘图库,它主要用于二维绘图,当然也可以进行简单的三维绘图.它不但提供了一整套和 Matl ...
- (转)Python数据分析之numpy学习
原文:https://www.cnblogs.com/nxld/p/6058572.html https://morvanzhou.github.io/tutorials/data-manipulat ...
- Python数据分析之pandas学习
Python中的pandas模块进行数据分析. 接下来pandas介绍中将学习到如下8块内容:1.数据结构简介:DataFrame和Series2.数据索引index3.利用pandas查询数据4.利 ...
- Python数据分析之numpy学习
Python模块中的numpy,这是一个处理数组的强大模块,而该模块也是其他数据分析模块(如pandas和scipy)的核心. 接下面将从这5个方面来介绍numpy模块的内容: 1)数组的创建 2)有 ...
- python数据分析入门——matplotlib的中文显示问题&最小二乘法
正在学习<用python做科学计算>,在练习最小二乘法时遇到matplotlib无法显示中文的问题.查资料,感觉动态的加上几条语句是最好,这里贴上全部的代码. # -*- coding: ...
- python数据分析使用matplotlib绘图
matplotlib绘图 关注公众号"轻松学编程"了解更多. Series和DataFrame都有一个用于生成各类图表的plot方法.默认情况下,它们所生成的是线形图 %matpl ...
- python库之matplotlib学习---关于坐标轴
首先定·定义x, y创建一个figure import numpy as np import matplotlib.pyplot as plt x = np.linspace(-1, 1, 10) y ...
- 08:Python数据分析之pandas学习
1.1 数据结构介绍 参考博客:http://www.cnblogs.com/nxld/p/6058591.html 1.pandas介绍 1. 在pandas中有两类非常重要的数据结构,即序列Ser ...
- Python数据分析之pandas学习(基础操作)
一.pandas数据结构介绍 在pandas中有两类非常重要的数据结构,即序列Series和数据框DataFrame.Series类似于numpy中的一维数组,除了通吃一维数组可用的函数或方法,而且其 ...
随机推荐
- 【JAVA】使用Aphache poi操作EXCEL 笔记
1 下载poi,地址 http://poi.apache.org/ 选择3.9版本. 2 刚开始尝试 把poi.jar放在D:\Program Files\java\jdk1.6.0_20\lib(不 ...
- 白鹭引擎 - 碰撞检测 ( hitTestPoint )
1, 矩形碰撞检测 class Main extends egret.DisplayObjectContainer { /** * Main 类构造器, 初始化的时候自动执行, ( 子类的构造函数必须 ...
- jquery-menu-aim插件实现二级导航
jquery-menu-aim插件是实现二级导航亚马逊式三角滑动的强力工具,它在性能上极佳,快速滑动,基本无延迟效果,源码位置见对应作者的github,接下来附上样例代码: $(function () ...
- +load +initialize
+load方法 在app启动的时候各个类的+load方法都会被调用,+load方法不是通过消息机制调用的,它是直接调用的,因此无论是在子类或者category中复写此方法,复写的+load方法都会被调 ...
- mui init 出现无法引入子页面问题
1. 检查项目中是否重复出现了 mui.init() 函数; mui.init({ subpages: [{ styles: { // top: "44px", top: &quo ...
- js函数的创建
1.js 函数的创建有几种方式: 1.1 直接声明 1.2 创建匿名函数,然后赋值 1.3 声明函数,然后赋值给变量 1.4 使用1.3 得到的变量再赋值给变量 1.5 使用函数对象创建函数 < ...
- postman 的基础使用
https://blog.csdn.net/fxbin123/article/details/80428216
- javascript中函数作用域和声明提前
javascript不像java等其他强类型语句,没有块级作用域(括号内的代码都有自己的作用域,变量在声明它们的代码段之外不可见)一说,但有自己的独特地方,即函数作用域. 函数作用域:变量在声明它们的 ...
- U3D的结构体堆分配栈分配
ST ot;//分配在栈上 ST[] arrt = new ST[2];//分配在堆上,因为数组是引用
- 趣味编程:静夜思(Python版)
from itertools import groupby def verticalWriting(txt, offset): l = lambda x: x[0] % offset for (_, ...
