MPC&MAGIC

MPC: Popularity-based Caching Strategy for Content Centric Networks

MPC： most popular content

　　　MPC主要思想是在缓存机制中，仅仅缓存popular的content，虽然只缓存部分内容，但是仍然提升了缓存性能，同时节约了缓存资源（缓存空间，带宽，缓存操作次数）

　　　在MPC中引入了几个新的概念：

　　　　　　Popular Table :记录popular content的name和popularcount

　　　　　　Popular Threshold : popular阈值，一旦content的请求次数，达到阈值，这个content标记为popular content

　　　　　　Suggestion : 含有popular content发送给邻居节点，建议邻居节点缓存popular content

　　　　　　Reset Value : 邻居节点缓存popular content后，这时防止邻居节点同一内容持续的洪泛请求

　　　下图是MPC缓存机制的基本过程：

　　　　

　　　　如图节点A先请求数据e1，节点B,A,C请求数据d1，内容e1的popular值为1，内容d1的popular值为3，假设popular阈值为2。

　　那么d1就为popular content。这时缓存d1的节点D向邻居节点发出Suggestion（缓存内容d1），节点C,E缓存内容d1。

　　　　如果此时A节点旁有个邻居节点M，节点M请求内容d1，那么A将返回数据d1而不是D，同时D将会将d1的popular值重置。

MAGIC: a Distributed MAx-Gain In-networkCaching Strategy in Information-Centric Networks

MAGIC：MAX-Gain In-network Caching

　　　　数据传送路径上的分布式缓存策略。通过考虑内容的popularity和减少跳数的结合减少带宽的浪费，同时考虑了缓存替换来减少缓存的操作。

　　　　cache palcement gain:节点在缓存中缓存新内容的gain的值

　　　　cache replacement penalty:节点将内容从缓存中驱逐的loss值

　　　　这两个值是减少缓存操作的次数

　　1.

　　　　

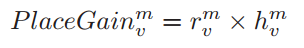
　　　　　　：节点v缓存请求内容m的缓存替换增益（gain）

　　　　　　：节点v请求内容m的请求速率（每秒发送INTERTEST messages的个数）

　　　　　　：从节点v到可以返回内容的节点之间的条数

　　　　

　　　　：定义为所有缓存内容对象的最小带宽消耗节省

　　　　如果缓存一个新的内容的增益值（gain）小于替换任何缓存内容的代价，那么这个内容将被缓存，同时其他内容不会被替换。

　　2.分布式缓存策略

　　　　分布式缓存策略需要在数据传送路径的沿途寻找最好的palace来缓存内容

　　

　　　　　　　　　　　　

　　上图的伪代码和图说明了MAGIC缓存的操作过程：

　　　　寻找数据传输路径上缓存内容的节点：我们用content m的最大的LocalGain来确定节点。当请求内容m时INTEREST message发送同时

　　　　INTEREST message头部的MaxGain的值置0，每个路由收到INTEREST message，计算自己的，将自己的值和INTEREST message

　　　　头部的MaxGain进行比较，如果大于MaxGain则，MaxGain更新为。

　　　　当INTEREST message到达服务器或者到达缓存内容m的节点后，MaxGain为最大值。DATA message中记录MaxGain的，DATA message

　　　　在返回的途中将与MaxGain向比较，如果相等，则此节点缓存内容m。