【C#数据结构系列】栈和队列

一：栈

　　栈和队列也是线性结构，线性表、栈和队列这三种数据结构的数据元素以及数据元素间的逻辑关系完全相同，差别是线性表的操作不受限制，而栈和队列的操作受到限制。栈的操作只能在表的一端进行，队列的插入操作在表的一端进行而其它操作在表的另一端进行，所以，把栈和队列称为操作受限的线性表。

1:栈的定义及基本运算

　　栈(Stack)是操作限定在表的尾端进行的线性表。表尾由于要进行插入、删除等操作，所以，它具有特殊的含义，把表尾称为栈顶（Top），另一端是固定的，叫栈底（Bottom）。当栈中没有数据元素时叫空栈(Empty Stack)。

　　栈通常记为：S= (a 1 ,a 2 ,…,a n )，S是英文单词stack的第 1 个字母。a 1 为栈底元素，a n 为栈顶元素。这n个数据元素按照a 1 ,a 2 ,…,a n 的顺序依次入栈，而出栈的次序相反，a n 第一个出栈，a 1 最后一个出栈。所以，栈的操作是按照后进先出(Last In First Out，简称LIFO)或先进后出(First In Last Out，简称FILO)的原则进行的，因此，栈又称为LIFO表或FILO表。

　　

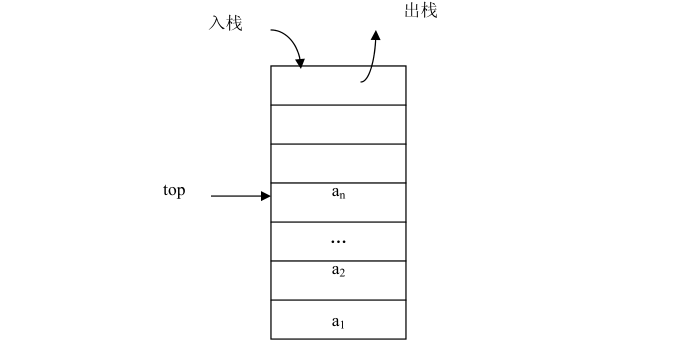
　　由于栈只能在栈顶进行操作，所以栈不能在栈的任意一个元素处插入或删除元素。因此，栈的操作是线性表操作的一个子集。栈的操作主要包括在栈顶插入元素和删除元素、取栈顶元素和判断栈是否为空等。

　　栈的接口定义如下所示：

 public interface IStack<T>
 {
     int GetLength(); //求栈的长度
     bool IsEmpty(); //判断栈是否为空
     void Clear(); //清空操作
     void Push(T item); //入栈操作
     T Pop(); //出栈操作
     T GetTop(); //取栈顶元素
 }

　　

2：栈的存储和运算实现

1、顺序栈：

　　用一片连续的存储空间来存储栈中的数据元素，这样的栈称为顺序栈(Sequence Stack)。类似于顺序表，用一维数组来存放顺序栈中的数据元素。

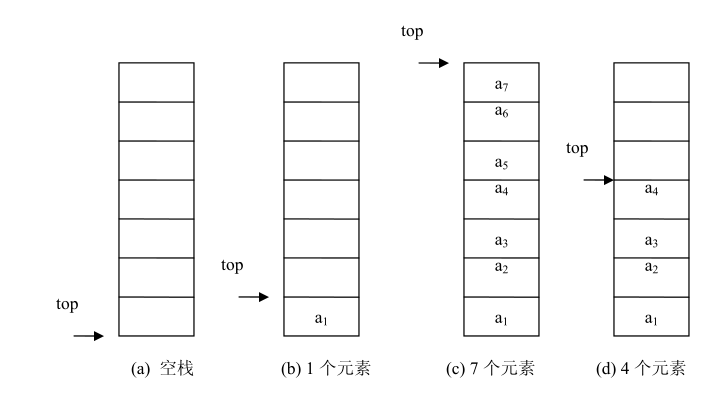
　　顺序栈类 SeqStack<T>的实现说明如下所示。

 public class SeqStack<T> : IStack<T>
     {
         private int maxsize; //顺序栈的容量
         private T[] data; //数组，用于存储顺序栈中的数据元素
         private int top; //指示顺序栈的栈顶
         //索引器
         public T this[int index]
         {
             get
             {
                 return data[index];
             }
             set
             {
                 data[index] = value;
             }
         }
         //容量属性
         public int Maxsize
         {
             get
             {
                 return maxsize;
             }
             set
             {
                 maxsize = value;
             }
         }
         //栈顶属性
         public int Top
         {
             get
             {
                 return top;
             }
         }
         //构造器
         public SeqStack(int size)
         {
             data = new T[size];
             maxsize = size;
             top = -;
         }
         //求栈的长度
         public int GetLength()
         {
             return top + ;
         }
         //清空顺序栈
         public void Clear()
         {
             top = -;
         }
         //判断顺序栈是否为空
         public bool IsEmpty()
         {
             if (top == -)
             {
                 return true;
             }
             else
             {
                 return false;
             }
         }
         //判断顺序栈是否为满
         public bool IsFull()
         {
             if (top == maxsize - )
             {
                 return true;
             }
             else
             {
                 return false;
             }
         }
         //入栈
         public void Push(T item)
         {
             if (IsFull())
             {
                 Console.WriteLine("Stack is full");
                 return;
             }
             data[++top] = item;
         }
         //出栈
         public T Pop()
         {
             T tmp = default(T);
             if (IsEmpty())
             {
                 Console.WriteLine("Stack is empty");
                 return tmp;
             }
             tmp = data[top];
             --top;
             return tmp;
         }
         //获取栈顶数据元素
         public T GetTop()
         {
             if (IsEmpty())
             {
                 Console.WriteLine("Stack is empty!");
                 return default(T);
             }
             return data[top];
         }
     }

2、链栈　　

　　栈的另外一种存储方式是链式存储，这样的栈称为链栈(Linked Stack)。链栈通常用单链表来表示，它的实现是单链表的简化。所以，链栈结点的结构与单链表结点的结构一样，如图 3.3 所示。由于链栈的操作只是在一端进行，为了操作方便，把栈顶设在链表的头部，并且不需要头结点。

　　链栈结点类(Node<T>)的实现如下：

　　

 public class Node<T>
     {
         private T data; //数据域
         private Node<T> next; //引用域
         //构造器
         public Node(T val, Node<T> p)
         {
             data = val;
             next = p;
         }
         //构造器
         public Node(Node<T> p)
         {
             next = p;
         }
         //构造器
         public Node(T val)
         {
             data = val;
             next = null;
         }
         //构造器
         public Node()
         {
             data = default(T);
             next = null;
         }
         //数据域属性
         public T Data
         {
             get
             {
                 return data;
             }
             set
             {
                 data = value;
             }
         }
         //引用域属性
         public Node<T> Next
         {
             get
             {
                 return next;
             }
             set
             {
                 next = value;
             }
         }
     }

　　

　　链栈类 LinkStack<T>的实现说明如下所示。

 public class LinkStack<T> : IStack<T>
     {
         private Node<T> top; //栈顶指示器
         private int num; //栈中结点的个数
         //栈顶指示器属性
         public Node<T> Top
         {
             get
             {
                 return top;
             }
             set
             {
                 top = value;
             }
         }
         //元素个数属性
         public int Num
         {
             get
             {
                 return num;
             }
             set
             {
                 num = value;
             }
         }
         //构造器
         public LinkStack()
         {
             top = null;
             num = ;
         }
         //求链栈的长度
         public int GetLength()
         {
             return num;
         }
         //清空链栈
         public void Clear()
         {
             top = null;
             num = ;
         }
         //判断链栈是否为空
         public bool IsEmpty()
         {
             if ((top == null) && (num == ))
             {
                 return true;
             }
             else
             {
                 return false;
             }
         }
         //入栈
         public void Push(T item)
         {
             Node<T> q = new Node<T>(item);
             if (top == null)
             {
                 top = q;
             }
             else
             {
                 q.Next = top;
                 top = q;
             }
             ++num;
         }
         //出栈
         public T Pop()
         {
             if (IsEmpty())
             {
                 Console.WriteLine("Stack is empty!");
                 return default(T);
             }
             Node<T> p = top;
             top = top.Next;
             --num;
             return p.Data;
         }
         //获取栈顶结点的值
         public T GetTop()
         {
             if (IsEmpty())
             {
                 Console.WriteLine("Stack is empty!");
                 return default(T);
             }
             return top.Data;
         }
     }

　　

3：C#中的栈

　　C#2.0 以下版本只提供了非泛型的 Stack 类，该类继承了 ICollection、IEnumerable 和 ICloneable 接口。C#2.0 提供了泛型的 Stack<T>类，该类继承了 IEnumerable<T>、ICollection 和 IEnumerable 接口。

二：队列

1：队列的定义及基本运算

　　队列(Queue)是插入操作限定在表的尾部而其它操作限定在表的头部进行的线性表。把进行插入操作的表尾称为队尾(Rear)，把进行其它操作的头部称为队头(Front)。当对列中没有数据元素时称为空对列(Empty Queue)。

　　队列通常记为：Q= (a 1 ,a 2 ,…,a n )，Q是英文单词queue的第 1 个字母。a 1 为队头元素，a n 为队尾元素。这n个元素是按照a 1 ,a 2 ,…,a n 的次序依次入队的，出对的次序与入队相同，a 1 第一个出队，a n 最后一个出队。所以，对列的操作是按照先进先出(First In First Out)或后进后出( Last In Last Out)的原则进行的，因此，队列又称为FIFO表或LILO表。队列Q的操作如下图。

　　

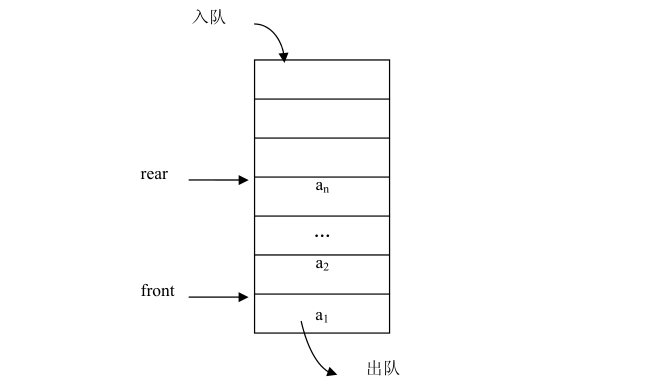
　　队列的操作是线性表操作的一个子集。队列的操作主要包括在队尾插入元素、在队头删除元素、取队头元素和判断队列是否为空等。与栈一样，队列的运算是定义在逻辑结构层次上的，而运算的具体实现是建立在物理存储结构层次上的。因此，把队列的操作作为逻辑结构的一部分，每个操作的具体实现只有在确定了队列的存储结构之后才能完成。队列的基本运算不是它的全部运算，而是一些常用的基本运算。

　　队列接口 IQueue<T>的定义如下所示。

 public interface IQueue<T>
     {
         int GetLength(); //求队列的长度
         bool IsEmpty(); //判断对列是否为空
         void Clear(); //清空队列
         void In(T item); //入队
         T Out(); //出队
         T GetFront(); //取对头元素
     }

2：队列的存储和运算实现

1、顺序队列　　

　　用一片连续的存储空间来存储队列中的数据元素，这样的队列称为顺序队列(Sequence Queue)。

　  类似于顺序栈，用一维数组来存放顺序队列中的数据元素。队头位置设在数组下标为 0 的端，用 front 表示；队尾位置设在数组的另一端，用 rear 表示。front 和 rear 随着插入和删除而变化。当队列为空时，front=rear=-1。下图是顺序队列的两个指示器与队列中数据元素的关系图。

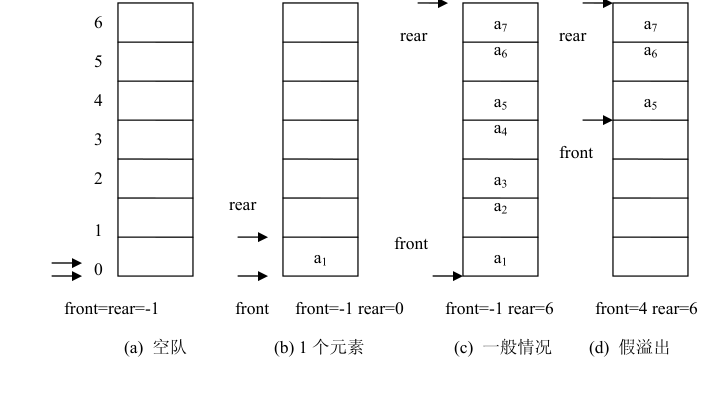
　　当有数据元素入队时，队尾指示器 rear 加 1，当有数据元素出队时，队头指示器 front 加 1。当 front=rear 时，表示队列为空，队尾指示器 rear 到达数组的上限处而 front 为-1 时，队列为满，如图(c)所示。队尾指示器 rear 的值大于队头指示器 front 的值，队列中元素的个数可以由 rear-front 求得。

　　由图 (d)可知，如果再有一个数据元素入队就会出现溢出。但事实上队列中并未满，还有空闲空间，把这种现象称为“假溢出”。这是由于队列“队尾入队头出”的操作原则造成的。解决假溢出的方法是将顺序队列看成是首尾相接的循环结构，头尾指示器的关系不变，这种队列叫循环顺序队列( Circular sequenceQueue )。循环队列如下图。

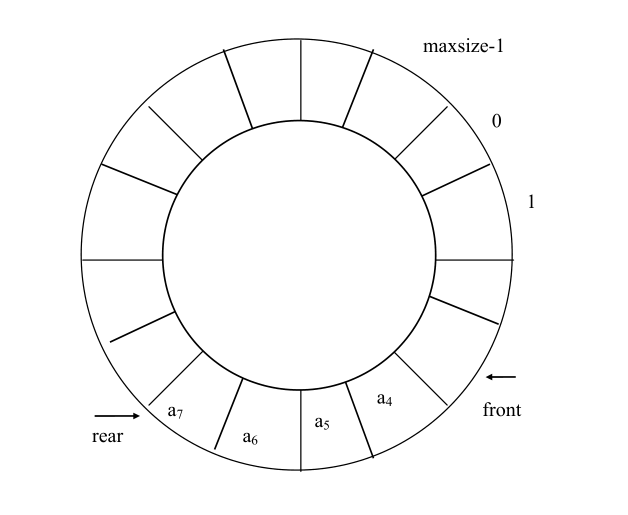
　　当队尾指示器 rear 到达数组的上限时，如果还有数据元素入队并且数组的第0 个空间空闲时，队尾指示器 rear 指向数组的 0 端。所以，队尾指示器的加 1 操作修改为：

　　　　　　　　　　rear = (rear + 1) % maxsize　　

　　队头指示器的操作也是如此。当队头指示器 front 到达数组的上限时，如果还有数据元素出队，队头指示器 front 指向数组的 0 端。所以，队头指示器的加1 操作修改为：

　　　　　　　　　　front = (front + 1) % maxsize

2：循环顺序队列操作示意图如下

　　

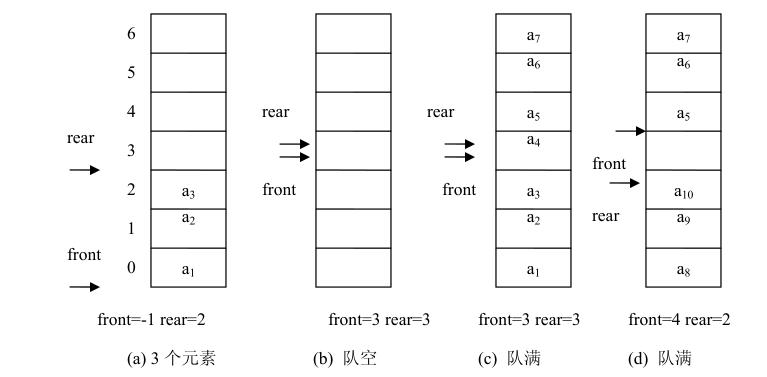
　　由图可知，队尾指示器 rear 的值不一定大于队头指示器 front 的值，并且队满和队空时都有 rear=front。也就是说，队满和队空的条件都是相同的。解决这个问题的方法一般是少用一个空间，如图 (d)所示，把这种情况视为队满。所以，判断队空的条件是：rear==front，判断队满的条件是：(rear + 1)% maxsize==front。求循环队列中数据元素的个数可由(rear-front+maxsize)%maxsize公式求得。

 public class CSeqQueue<T> : IQueue<T>
     {
         private int maxsize; //循环顺序队列的容量
         private T[] data; //数组，用于存储循环顺序队列中的数据元素
         private int front; //指示循环顺序队列的队头
         private int rear; //指示循环顺序队列的队尾
         //索引器
         public T this[int index]
         {
             get
             {
                 return data[index];
             }
             set
             {
                 data[index] = value;
             }
         }
         //容量属性
         public int Maxsize
         {
             get
             {
                 return maxsize;
             }
             set
             {
                 maxsize = value;
             }
         }
         //队头属性
         public int Front
         {
             get
             {
                 return front;
             }
             set
             {
                 front = value;
             }
         }
         //队尾属性
         public int Rear
         {
             get
             {
                 return rear;
             }
             set
             {
                 rear = value;
             }

         }
         //构造器
         public CSeqQueue(int size)
         {
             data = new T[size];
             maxsize = size;
             front = rear = -;
         }
         //求循环顺序队列的长度
         public int GetLength()
         {
             return (rear - front + maxsize) % maxsize;
         }
         //清空循环顺序队列
         public void Clear()
         {
             front = rear = -;
         }
         //判断循环顺序队列是否为空
         public bool IsEmpty()
         {
             if (front == rear)
             {
                 return true;
             }
             else
             {
                 return false;
             }
         }
         //判断循环顺序队列是否为满
         public bool IsFull()
         {
             if ((rear + ) % maxsize == front)
             {
                 return true;
             }
             else
             {
                 return false;
             }
         }
         //入队
         public void In(T item)
         {
             if (IsFull())
             {
                 Console.WriteLine("Queue is full");
                 return;
             }
             data[++rear] = item;
         }
         //出队
         public T Out()
         {
             T tmp = default(T);
             if (IsEmpty())
             {
                 Console.WriteLine("Queue is empty");
                 return tmp;
             }
             tmp = data[++front];
             return tmp;
         }
         //获取队头数据元素
         public T GetFront()
         {
             if (IsEmpty())
             {
                 Console.WriteLine("Queue is empty!");
                 return default(T);
             }
             return data[front + ];
         }
     }

　　

3：链队列

　　队列的另外一种存储方式是链式存储，这样的队列称为链队列(LinkedQueue)。同链栈一样，链队列通常用单链表来表示，它的实现是单链表的简化。所以，链队列的结点的结构与单链表一样，由于链队列的操作只是在一端进行，为了操作方便，把队头设在链表的头部，并且不需要头结点。

节点示意图：

　　　　　　　　

链队列示意图：

　　　　　　　　　　

　　把链队列看作一个泛型类，类名为 LinkQueue<T>。LinkQueue<T>类中有两个字段 front 和 rear，表示队头指示器和队尾指示器。由于队列只能访问队头的数据元素，而链队列的队头指示器和队尾指示器又不能指示队列的元素个数，所以，与链栈一样，在 LinkQueue<T>类增设一个字段 num 表示链队列中结点的个数。链队列类 LinkQueue<T>的实现说明如下所示。

　　

 public class LinkQueue<T> : IQueue<T>
     {
         private Node<T> front; //队列头指示器
         private Node<T> rear; //队列尾指示器
         private int num; //队列结点个数
         //队头属性
         public Node<T> Front
         {
             get
             {
                 return front;
             }
             set
             {
                 front = value;
             }
         }
         //队尾属性
         public Node<T> Rear
         {
             get
             {
                 return rear;
             }
             set
             {
                 rear = value;
             }
         }
         //队列结点个数属性
         public int Num
         {
             get
             {
                 return num;
             }
             set
             {
                 num = value;
             }
         }
         //构造器
         public LinkQueue()
         {
             front = rear = null;
             num = ;
         }
         //求链队列的长度
         public int GetLength()
         {
             return num;
         }
         //清空链队列
         public void Clear()
         {
             front = rear = null;
             num = ;
         }
         //判断链队列是否为空
         public bool IsEmpty()
         {
             if ((front == rear) && (num == ))
             {
                 return true;
             }
             else
             {
                 return false;
             }
         }
         //入队
         public void In(T item)
         {
             Node<T> q = new Node<T>(item);
             if (rear == null)
             {
                 rear = q;
             }
             else
             {
                 rear.Next = q;
                 rear = q;
             }
             ++num;
         }
         //出队
         public T Out()
         {
             if (IsEmpty())
             {
                 Console.WriteLine("Queue is empty!");
                 return default(T);
             }
             Node<T> p = front;
             front = front.Next;
             if (front == null)
             {
                 rear = null;
             }
             --num;
             return p.Data;
         }
         //获取链队列头结点的值
         public T GetFront()
         {
             if (IsEmpty())
             {
                 Console.WriteLine("Queue is empty!");
                 return default(T);
             }
             return front.Data;
         }
     }

　　3.1：C# 中的队列

　　C#2.0 以下版本只提供了非泛型的 Queue 类，该类继承了 ICollection、IEnumerable 和 ICloneable 接口。C#2.0 提供了泛型的 Queue<T>类，该类继承了 IEnumerable<T>、ICollection 和 IEnumerable 接口。以下程序说明了泛型Queue<T>类的主要方法，并对在我们自定义的队列类中没有出现的成员方法进行了注释，关于泛型 Queue<T>类的更具体的信息，读者可参考.NET Framework的有关书籍。　　

三 ： 小结

　　栈和队列是计算机中常用的两种数据结构，是操作受限的线性表。栈的插入和删除等操作都在栈顶进行，它是先进后出的线性表。队列的删除操作在队头进行，而插入、查找等操作在队尾进行，它是先进先出的线性表。与线性表一样，栈和队列有两种存储结构，顺序存储的栈称为顺序栈，链式存储的栈称为链栈。顺序存储的队列称为顺序对列，链式存储的队列称为链队列。

　　为解决顺序队列中的假溢出问题，采用循环顺序队列，但出现队空和队满的判断条件相同的问题，判断条件都是：front==rear。采用少用一个存储单元来解决该问题。此时，队满的判断条件是：(rear+1)%maxsize==front，判断队空的条件是：rear==front。

　　栈适合于具有先进后出特性的问题，如括号匹配、表达式求值等问题；队列适合于具有先进先出特性的问题，如排队等问题。