BP算法基本原理推导----《机器学习》笔记
前言
多层网络的训练需要一种强大的学习算法,其中BP(errorBackPropagation)算法就是成功的代表,它是迄今最成功的神经网络学习算法。
今天就来探讨下BP算法的原理以及公式推导吧。
神经网络
先来简单介绍一下神经网络,引入基本的计算公式,方便后面推导使用
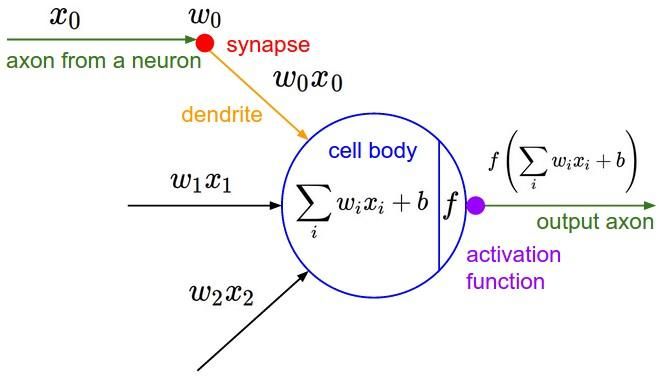
图1 神经网络神经元模型
图1就是一个标准的M-P神经元模型。
【神经元工作流程】
每个神经元接受n个(图1中只有3个)来自其他神经元或者直接输入的输入信号(图1中分别为x0,x1,x2),这些输入信号分别与每条“神经”的权重相乘,并累加输入给当前神经元。每个神经元设定有一个阈值θ(图1中的b),累计值需要减去这个阈值,并且将最终结果通过“激活函数”(图1中的f)挤压到(0,1)范围内,最后输出。
总结一下,神经元的工作流程主要有3步:
①累计输入的信号与权重。
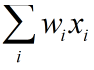
②将权重与设定的阈值相减

③将第2步得出的结果送给激活函数(一般是sigmoid函数),输出
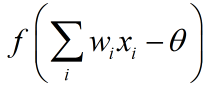
【多层前馈神经网络】
将上面的神经元按照一定的层次结构连接起来,就得到了神经网络。
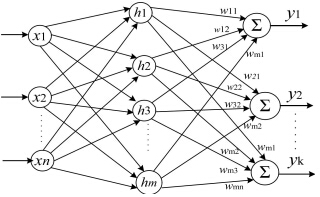
图2 多层前馈神经网络
图2显示的是一个3层(1个输入层,1个隐藏层,1个输出层)的神经网络。
像这样的形成层级结构,每层神经元与下一层神经元全连接(每层的每个神经元到下一层的每个神经元都有连接),神经元之间不存在同层连接,也不存在跨层连接的神经网络通常被称为“多层前馈神经网络”。
【神经网络工作流程】
假定有数据集D:
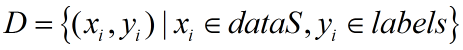
输入神经网络,同样假定就是图2这个3层前馈神经网络,我们来列一下,图2这个网络要通过这些训练集来训练得到多少个参数。
图2的神经网络有n个输入神经元(记为x1、x2....xn)、m个隐藏层神经元(记为h1,h2,...,hm),k个输出神经元(记为y1,y2,...,yk),通过训练,我们要获得下面几种数值
①输入层到隐藏层的权值:n x m 个
②隐藏层到输出层的权值:m x k 个
③m个隐藏层阈值与k个输出层阈值
训练完成后,通过测试集样例与训练出的参数,可以直接得到输出值来判断所属分类(分类问题)
BP算法
神经网络的运行过程清楚了,那么训练过程是怎么样的呢?
我们知道,训练的任务是:
通过某种算法,习得上面所讲的n x m + m x k + m + k = (n+k+1) x m + k 个参数
这里我们使用的就是BP算法。
先来根据神经元工作流程来定义几个量,这里再贴一下修改后的神经网络流程图
图3 3层前馈神经网络图
【定义】
第i个输入神经元到第j个隐藏层神经元的权重:Vij
第i个隐藏层神经元到第j个输出层神经元的权重:Wij
第i个隐藏层神经元的输出:bi
第i个输出层的阈值:θi
第j个隐藏层神经元的输入:

第q个输出神经元的额输入:

假定通过我们的神经网络,对于训练样例 网络输出为
网络输出为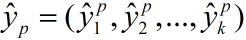
假定完美输出应该为 ,例如,对于k分类问题,若训练样例p属于第1类,则yp=(1,0,0,0...,0)
,例如,对于k分类问题,若训练样例p属于第1类,则yp=(1,0,0,0...,0)
那么一轮训练我们的均方误差为:
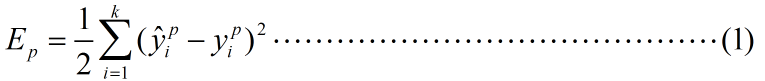
实际上
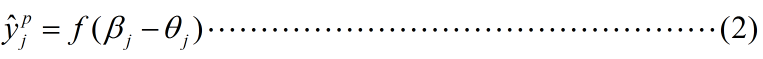
其中f函数为sigmoid函数。
这下,我们的目标就转化为:
寻得一组合适的参数序列,使得(1)式的值(均方误差)最小。
在我的上一篇随笔里也提到过这个问题,这种形式的问题比较适合使用梯度下降算法,BP正是采取了这个策略,以目标的负梯度方向对参数进行调整。
【梯度下降求解参数】
梯度下降的基本思想是:设定参数的初始值,通过一个学习速率η和当前梯度,来逐渐步进参数,以求拟合一个局部最优的参数
一般的参数迭代过程如下:
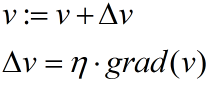
不清楚梯度下降算法的可以看一下我另一篇随笔:http://www.cnblogs.com/HolyShine/p/6403116.html
神经网络的一次迭代,就是参数的一次“步进”。
接下来我们使用梯度下降分别推导几个参数的迭代公式
我们以隐藏层中第h个神经元为参照对象,求解他的输入权重V和输出权重W,以及阈值γ;以输出层中第j个神经元为输出参照,求解他的阈值θ
<隐藏层到输出层的权重Whj>
根据梯度下降算法,权重参数的步进为:
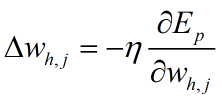
由复合函数求导公式以及式(1)式(2):

其中,第二项是sigmoid函数求导,由于sigmoid函数有如下的性质:
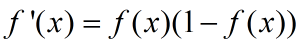
所以

第一项和第三项的推导也列在这里
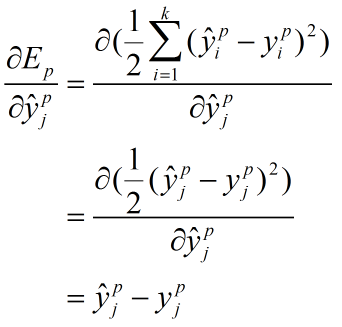
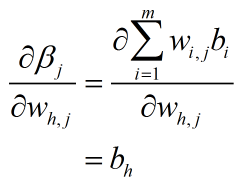
最终(3)式变为:
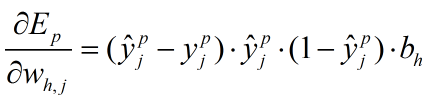
这些量都是一轮训练中已知的,因此可以解得梯度的大小,用于参数的更新工作
其他参数的求解基本一致。
BP算法基本原理推导----《机器学习》笔记的更多相关文章
- BP算法的推导
反向传播算法的推导 如图为2-layers CNN,输入单元下标为i,数量d:隐层单元下表j,数量\(n_H\):输出层下表k,单元数量c 1.目标 调整权系数\(w_{ji}\),\(w_{kj}\ ...
- 跟我学算法-xgboost(集成算法)基本原理推导
1.构造损失函数的目标函数 2.对目标函数进行泰勒展开 3.把样本遍历转换成叶子节点遍历,合并正则化惩罚项 4.求wj进行求导,使得当目标函数等于0时的wj的值 5.将求解得到的wj反导入方程中,解得 ...
- 从 0 开始机器学习 - 神经网络反向 BP 算法!
最近一个月项目好忙,终于挤出时间把这篇 BP 算法基本思想写完了,公式的推导放到下一篇讲吧. 一.神经网络的代价函数 神经网络可以看做是复杂逻辑回归的组合,因此与其类似,我们训练神经网络也要定义代价函 ...
- 一文彻底搞懂BP算法:原理推导+数据演示+项目实战(上篇)
欢迎大家关注我们的网站和系列教程:http://www.tensorflownews.com/,学习更多的机器学习.深度学习的知识! 反向传播算法(Backpropagation Algorithm, ...
- 深度学习——前向传播算法和反向传播算法(BP算法)及其推导
1 BP算法的推导 图1 一个简单的三层神经网络 图1所示是一个简单的三层(两个隐藏层,一个输出层)神经网络结构,假设我们使用这个神经网络来解决二分类问题,我们给这个网络一个输入样本,通过前向运算得到 ...
- 机器学习入门学习笔记:(一)BP神经网络原理推导及程序实现
机器学习中,神经网络算法可以说是当下使用的最广泛的算法.神经网络的结构模仿自生物神经网络,生物神经网络中的每个神经元与其他神经元相连,当它“兴奋”时,想下一级相连的神经元发送化学物质,改变这些神经元的 ...
- [DL学习笔记]从人工神经网络到卷积神经网络_1_神经网络和BP算法
前言:这只是我的一个学习笔记,里边肯定有不少错误,还希望有大神能帮帮找找,由于是从小白的视角来看问题的,所以对于初学者或多或少会有点帮助吧. 1:人工全连接神经网络和BP算法 <1>:人工 ...
- 误差逆传播(error BackPropagation, BP)算法推导及向量化表示
1.前言 看完讲卷积神经网络基础讲得非常好的cs231后总感觉不过瘾,主要原因在于虽然知道了卷积神经网络的计算过程和基本结构,但还是无法透彻理解卷积神经网络的学习过程.于是找来了进阶的教材Notes ...
- 猪猪的机器学习笔记(十四)EM算法
EM算法 作者:樱花猪 摘要: 本文为七月算法(julyedu.com)12月机器学习第十次次课在线笔记.EM算法全称为Expectation Maximization Algorithm,既最大 ...
随机推荐
- WPF中的数据绑定(初级)
关于WPF中的数据绑定,初步探讨 数据绑定属于WPF中比较核心的范畴,以下是对WPF中数据绑定的一个初步探讨.个人感觉还是带有问题性质的叙述比较高效,也比较容易懂 第一,什么是数据绑定? 假定有这么一 ...
- JavaSE基础知识(5)—面向对象(对象数组和对象关联)
一.对象数组 1.说明 数组的定义类型为对象类型 2.动态初始化 1.声明并开辟空间 Person[] pers = new Person[长度];2.赋值 for(int i=0;i<pers ...
- redis常用服务安装部署
常用服务安装部署 学了前面的Linux基础,想必童鞋们是不是更感兴趣了?接下来就学习常用服务部署吧! 安装环境: centos7 + vmware + xshell 即将登场的是: mysql(m ...
- 直接插入排序(js版)
直接插入排序(从小到大) 基本思想:将一个记录插入到已经排好序的有序表中,得到一个新的,记录数加1的有序表. function insertSort(arr){ var i,j,temp=0; for ...
- elementUI中表格中表单的验证
表格中的表单验证,就是在将表格放在表单中,将表格绑定的数据也放在表单中. 最重要的是要给表格中需要验证的字段动态添加prop,再给其绑定规则. <el-form :model="tab ...
- 根据select出来的数据进行update
update t_tbl_desc set num=b.num from t_tbl_desc a, (select distinct(name) as name,count(name) num fr ...
- 抖音分享和授权(iOS)
准备工作 注册appkey 抖音开放平台 集成sharesdk 下载地址 Xcode配置:urlScheme为注册的appkey, 白名单:douyinsharesdk ,douyinopensdk ...
- PM学习梳理--建模型
- SQL视图命名规则:一般以V_xxx_xxxxxx
- XML文件的解析—DOM、SAX
一.DOM 解析 思路:获得Document对象,遍历其中节点获得需要的内容 要点: Document : DocuemntBuilderFactory --newDocumentBuilder - ...
