Sigma Function

　　做完这道题，我明白了人生的一个巨大道理，那就是： 其他题研究两下，做出来几百行。数论码字前研究半天，做出来十几二十行。做完特别没有成就感。。。

　　首先说下这题题意：首先，定义一个函数f[n]，即为他所有因子和，他自带一个叼叼的公式

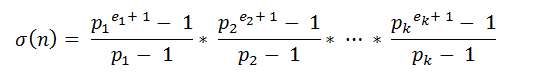，然后问对一个给定的n，从1到n，他们的f[n]中有几个是偶数。。。pi 是n的素数因子，ei 是对应素因子的个数。。

我当时的思路历程： 首先比较简单，如果这k个式子全是奇数，那么f[n]是奇数，只要出现一个偶数，那么结果便是偶数，所以答案应该非常接近n，n大小在1万亿，所以不可能是普通遍历。。同时偶数非常多，那么可以转换为求奇数个数。。。

对于所有的素数。。如果p为2，那么那个式子一定为奇数，所以假如某个数a 满足条件，那么多给他一个素因子2，他肯定也满足条件，无论多给几个，他都满足条件（当然，最后发现只需要多给一个）    ，然后对于不是2的素数，可以发现当ei+1为奇数的时候，也就是pi这个素因子出现偶数次的时候，这一项也为奇数。那么可以想来对于某个数，他是平方得来的，那么他一定满足条件。。比如： 225。 225是的15的平方，虽然他的素因子3、5都不是2那么直接，但由于他是平方得来的，那么分解出来是 3*3*5*5,所以每一项都是奇数，所以225满足条件。基础知道了。现在拿一些数找找规律（虽然当时我是找到规律才明白的思路0.0），我当时列举了前一百个。。可以发现，1*1 2*2 3*3 4*4 5*5 。。。 都满足条件（这是必然的），那么再细化一下，对于3的次方倍来说： 9 27 81 。。 其中27因为素因子3出现次数为奇数次，不满足条件，舍去，剩下的9、81就可以看成是3的平方和9的平方。。对于每个数都是这个规律，也就是出现奇数次不满足条件。所以我们的第二个推论可以验证了这部分的数量。。同时，对于每个平方数 如 9 那么 18 也满足条件，但36虽然也满足条件，却不需要再在这个时候记入计算，因为36还等于6*6，也就是（2*3）*（2*3），所以，也可以看出规律，对于每个平方数的2倍也满足条件。。。那么，正是因为我们不去重复计算36，所以我们算出来的不会有重叠的。。

　　co=2*((int)sqrt(a));  短短一句就可以解决。。。。（我当时想了半天，真正意义上的半天，从下午到深夜。。）

　　最最后，要解决的就是多算的。。。比如：n=100，那么10 * 10==100，我们不能再去算2*10*10，但相信前面一段出来，这个也就没什么难度了。。。

　　AC代码：

 #include<stdio.h>
 #include<math.h>
 int fun(long long a)
 {
   int co=;
   int s=(int )sqrt(a);
   while(s>)
   {
     if((long long)s*s*>a) co++;
     else break;
     s--;
   }
   return co;
 }
 int main()
 {
   long long a;
   int t,co=,g=;
   scanf("%d",&t);
   while(t--)
   {
     scanf("%lld",&a);
     co=*((int)sqrt(a));
     co-=fun(a);
     printf("Case %d: %lld\n",g++,a-co);
   }
   return ;
 }

哎，没怎么优化