NOIP2008双栈排序（贪心）

题目描述

Tom最近在研究一个有趣的排序问题。如图所示，通过2个栈S1和S2，Tom希望借助以下4种操作实现将输入序列升序排序。

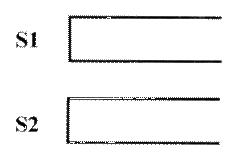
操作a

如果输入序列不为空，将第一个元素压入栈S1

操作b

如果栈S1不为空，将S1栈顶元素弹出至输出序列

操作c

如果输入序列不为空，将第一个元素压入栈S2

操作d

如果栈S2不为空，将S2栈顶元素弹出至输出序列

如果一个1~n的排列P可以通过一系列操作使得输出序列为1，2，…，(n-1)，n，Tom就称P是一个“可双栈排序排列”。例如(1,3,2,4)就是一个“可双栈排序序列”，而(2,3,4,1)不是。下图描述了一个将(1,3,2,4)排序的操作序列：<a,c,c,b,a,d,d,b>

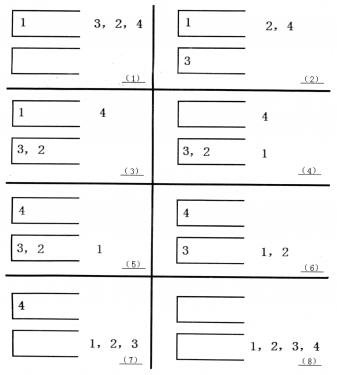
当然，这样的操作序列有可能有几个，对于上例(1,3,2,4)，<a,c,c,b,a,d,d,b>是另外一个可行的操作序列。Tom希望知道其中字典序最小的操作序列是什么。

Solution

先考虑如何判掉不合法的情况，对于一个数，如果它前面有一个数比他大，那他们不能在同一个栈里，我们可以在它们之间连一条边，那么连出来的这张图如果有奇环，就是不合法的。

再考虑对于一个合法解，如何是答案字典序最小。

我们对于一个联通块内让编号最小的点进一号栈，那么所有元素进入栈的编号就确定了，接下来按照题意模拟，有能弹出的元素就弹出。

但这样为什么能保证字典序最小？

考虑当二号栈有元素需要弹出，下一个元素要进一号栈，那么我们应该先让一号进入，二号弹出，我们的做法就出锅了。

所以要加特判

Code

#include<iostream>
#include<cstdio>
#define N  1009
using namespace std;
struct dd
{
    int n,to;
}an[N*N];
int a[N],co[N],head[N],tot,n,mi,p,tag,top1,top2,st1[N],st2[N];
bool vis[N];
inline void add(int u,int v)
{
    an[++tot].n=head[u];
    an[tot].to=v;
    head[u]=tot;
}
bool dfs(int u,int fa)
{
    vis[u]=;
    for(int i=head[u];i;i=an[i].n)
    if(an[i].to!=fa)
    {
      if(co[an[i].to]==-co[u])return ;
      co[an[i].to]=-co[u];
      if(!vis[an[i].to])if(!dfs(an[i].to,u))return ;
   }
   return ;
}
int main()
{
    scanf("%d",&n);
    for(int i=;i<=n;++i)scanf("%d",&a[i]);
    mi=0x3f3f3f3f;
    for(int i=n;i>=;--i)
    {
       for(int j=;j<i;++j)
          if(a[j]<a[i]&&a[j]>mi)add(j,i),add(i,j);
       mi=min(mi,a[i]);
    }
    for(int i=;i<=n;++i)
      if(!vis[i])
      {
        co[i]=;
        if(!dfs(i,))
        {
            printf("");
            return ;
        }
      }
      p=;
    for(int i=;i<=n;++i)
    {
        tag=co[i]==?:;
        if(tag==)
        {
         printf("a ");
         st1[++top1]=a[i];
        }
        else
        {
          printf("c ");
          st2[++top2]=a[i];
        }
        while(st1[top1]==p+||st2[top2]==p+)
        if(p+==st1[top1])printf("b "),p++,top1--;
        else printf("d "),p++,top2--;
    }
    return ;
}