CSAPC2008 skyline

一座山的山稜线由许多片段的45度斜坡构成，每一个片段不是上坡就是下坡。

*
    *   *  /\
*  /\  /\/   \
/\/  \/        \

在我们眼前的所见的任何宽度为n个单位的山稜形状，可以轻松地观察到所有山顶的位置。

请问有多少种山稜线的形状，使得所有山顶的位置由左而右非递减呢？

所有的山稜线都必须完整，也就是说左右两端都必须是高度为0的山脚，而且不能有任何山谷的位置隐没在地平线底下。

输入说明 ：

输入仅包含一个数字n，n一定会是偶数，因为会有相同片段数量的上坡以及下坡。

输出说明 ：

请输出山顶位置由左而右非递减的山稜线形状总数。
由于答案可能很大，你只要输出以十进位表示时，它的最后9位数即可。

范例输入 ：

6

范例输出 ：

4

提示 ：

佔总分20%的测试数据中 n<=60
佔总分40%的测试数据中 n<=200
佔总分100%的测试数据中 n<=3000

题解：

动态规划

记dp[i][j]表示长度为i+j，山稜最大高度为j时的方案数，那么它可以由以下两种状态转移过来。

1）dp[i-1][j-1]（在原图形的两侧分别加上一条线，如下图）

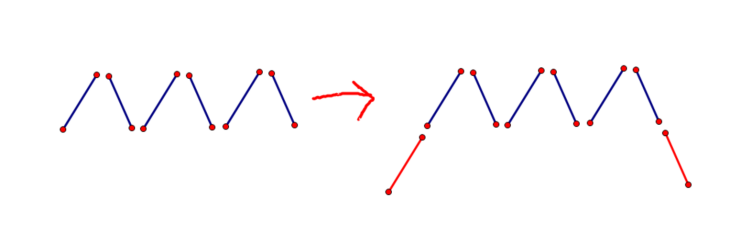
2）之前已经存在了的最大高度为j的山峰，在左边补上高度比它小的山峰而形成的，如下图

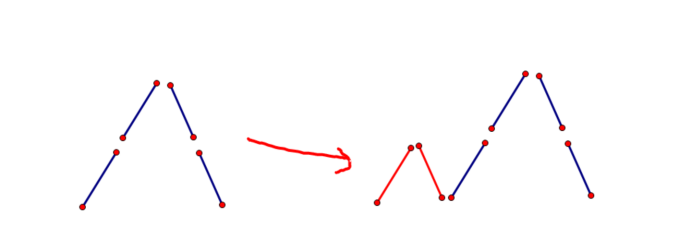
我们将情况2）通过一个前缀和数组sum[i][j]表示（表示长度不超过i+j且高度为j的方案数）

那么状态转移方程即为：dp[i][j]=dp[i-1][j-1]+sum[i-2][j]，

sum[i][j]=sum[i-1][j]+dp[i][j]

为了保证合法则必须有(i+j) mod 2=0

那么这题是不是结束了？并没有

在情况2）中，我们直接加上了sum[i-2][j]，这样做有什么问题吗？

我们考虑下面的图

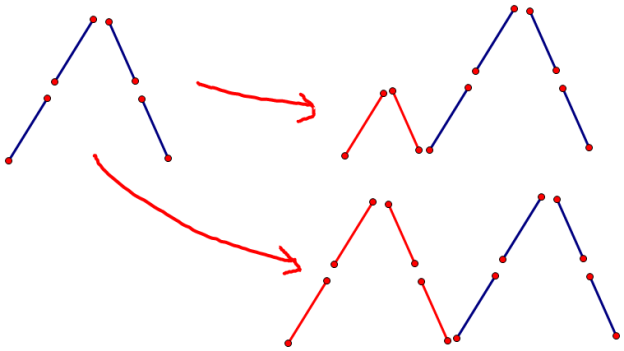
对于左面新添加的山稜，为了保证答案的合法，只能在它的旁边加上高度不超过当前最大高度的山稜，即下面的转移是不合法的

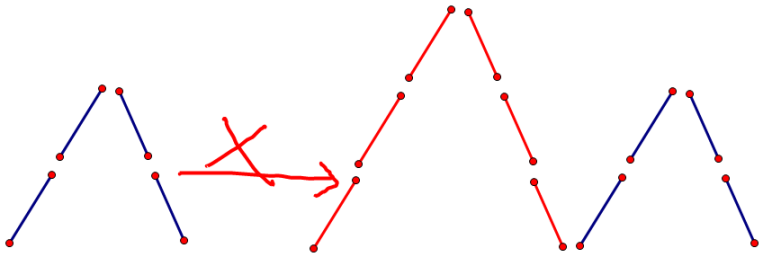
但是如果我们只是单纯的加上sum[i-2][j]是无法解决上面所提到的不合法的情况

即：我们在转移完了之后，要减去一部分不合法的情况

这些不合法的情况是：长度小于i-j，高度为j的所有山稜

所以在转移完成之后需要将sum[i-j-j-1][j]减去即可

最后答案：

程序：

 #include <stdio.h>

 #include <iostream>

 using namespace std;

 const int maxd=;

 int dp[][]={};

 int sum[][]={};

 int main() {

    int n,i,j,s;

    dp[][] = ;

    sum[][] = ;

    for( i=; i<=; i++ ) {

       for( j=; j<i; j++ ) {

          if((i+j)%==) {

             dp[i][j] = (dp[i-][j-]+sum[i-][j])%maxd;

             if(i-j-j->=) {

                dp[i][j] = (dp[i][j]-sum[i-j-j-][j])%maxd;

                if(dp[i][j]<) dp[i][j]+=maxd;

             }

          }

          sum[i][j] = (sum[i-][j]+dp[i][j])%maxd;

       }

       dp[i][i] = ;

       sum[i][i] = ;

    }

    scanf("%d",&n);

       s = ;

       for( i=; i<=n/; i++ ) {

          s = (s+dp[n-i][i])%maxd;

       }

       printf("%d\n",s);

    return ;

 }