MT【248】$f(x)=\dfrac{1}{x-1}+\dfrac{1}{x-b}$的性质
探讨函数$f(x)=\dfrac{1}{x-a}+\dfrac{1}{x-b}$其中$a<b$的几个性质
分析:
对称性:关于$(\dfrac{a+b}{2},0)$证明提示:$f(x)+f(a+b-x)=0$且定义域关于$(\dfrac{a+b}{2},0)$对称
单调性:单调递减区间$(-\infty,a),(a,b),(b,+\infty)$,证明提示:用单调性的定义
渐进性:$\lim\limits_{x\rightarrow-\infty}f(x)=0$;$\lim\limits_{x\rightarrow+\infty}f(x)=0$;
$\lim\limits_{x\rightarrow a^+}f(x)=+\infty$;$\lim\limits_{x\rightarrow a^-}f(x)=-\infty$
$\lim\limits_{x\rightarrow b^+}f(x)=+\infty$;$\lim\limits_{x\rightarrow b^-}f(x)=-\infty$
最后提供一张$a=1,b=2$时的图.
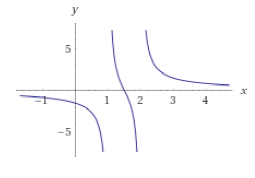
MT【248】$f(x)=\dfrac{1}{x-1}+\dfrac{1}{x-b}$的性质的更多相关文章
- (极值点偏移问题的几种方案)已知$\dfrac{\ln x_1}{x_1}=\dfrac{\ln x_2}{x_2}$,求证:$x_1+x_2>2\text{e}$.
第一个图适合在手机上操作(点击\(\checkmark\)显示/隐藏) 第二个图适合在电脑上操作(点击\(\checkmark\)显示/隐藏)
- MT【131】$a_{n+1}\cdot a_n=\dfrac 1n$
已知数列\(\{a_n\}\)满足\(a_1=1\),\(a_{n+1}\cdot a_n=\dfrac 1n\)(\(n\in\mathbb N^*\)). (1) 求证:\(\dfrac{a_{n ...
- MT【210】四点共圆+角平分线
(2018全国联赛解答最后一题)在平面直角坐标系$xOy$中,设$AB$是抛物线$y^2=4x$的过点$F(1,0)$的弦,$\Delta{AOB}$的外接圆交抛物线于点$P$(不同于点$A,O,B$ ...
- MT【330】u,v,w法
已知$a^2+b^2+c^2=1$求$abc(a+b+c)$的最小值.(2018辽宁预赛解答压轴题) 不妨设$a+b+c=3u,ab+bc+ca=3v^2,abc=w^3$,令$u^2=tv^2$要求 ...
- MT【329】二次函数系数的最大最小
已知二次函数$f(x)=ax^2+bx+c$有零点,且$a+b+c=1$ 若$t=\min\{a,b,c\}$求$t$的最大值. 分析:由$a,c$的对称性,不妨$c\ge a$即$2a+b\le1$ ...
- MT【321】分类线性规划
若二次函数$f(x)=ax^2+bx+c(a,b,c>0)$有零点,则$\min\{\dfrac{b+c}{a},\dfrac{c+a}{b},\dfrac{a+b}{c}\}$ 的最大值为__ ...
- MT【298】双参数非齐次
若函数$f(x)=x^2+(\dfrac{1}{3}+a)x+b$在$[-1,1]$上有零点,则$a^2-3b$的最小值为_____ 分析:设零点为$x_0$,则$b=-x^2_0-(\dfrac{1 ...
- MT【296】必要性探路
已知$a,b\in R.f(x)=e^x-ax+b$,若$f(x)\ge1$恒成立,则$\dfrac{b-a}{a}$的取值范围_____ 提示:答案:$[-1,\infty)$取$x=0,b\ge0 ...
- MT【290】内外圆求三角最值
求$\sqrt{\dfrac{5}{4}-\sin x}+2\sqrt{\dfrac{9}{4}+\cos x-\sin x}$的最小值. 提示:$\sqrt{\dfrac{5}{4}-\sin x} ...
随机推荐
- 14-Requests+正则表达式爬取猫眼电影
'''Requests+正则表达式爬取猫眼电影TOP100''''''流程框架:抓去单页内容:利用requests请求目标站点,得到单个网页HTML代码,返回结果.正则表达式分析:根据HTML代码分析 ...
- Dapper.NET
关于Dapper.NET的相关论述 年少时,为何不为自己的梦想去拼搏一次呢?纵使头破血流,也不悔有那年少轻狂.感慨很多,最近事情也很多,博客也很少更新了,毕竟每个人都需要为自己的生活去努力. 最近 ...
- react初入门
<!DOCTYPE html> <html lang="en"> <head> <meta charset="UTF-8&quo ...
- Chrome 离线安装插件的办法
参考url 学习网址 https://blog.csdn.net/weixin_39068791/article/details/81411938 插件下载地址: http://www.lanfans ...
- oracle建表流程
--创建表空间test1 create tablespace test1 datafile 'd:\test1.dbf' size 100m autoextend on next 10m --创建用户 ...
- Eclipse在写java时的BUG
要把这个关掉
- centOS7防火墙关闭失败问题
CentOS7命令: 查看防火墙状态:firewall-cmd --state 关闭防火墙:systemctl stop firewalld.service 禁止开机自启:systemctl disa ...
- CSS3 background-size属性兼容
background-size是CSS3新增的属性,但是IE8以下还是不支持 background-size:contain; // 缩小图片来适应元素的尺寸(保持像素的长宽比):background ...
- RedHat Enterprise Linux 6.4使用yum安装出现This system is not registered to Red Hat Subscription Management
我虚拟机安装的系统是RedHat Enterprise Linux 6.4-i686,是32位的.使用yum命令安装软件时候出现以下错误: This system is not registered ...
- git简介及安装(win10)
一句话介绍git Git是Linus Torvalds编写,目前是世界上最先进的分布式版本控制系统. git能干什么? 代码备份.还原,版本管理,分支管理,解决冲突,协同开发... 安装git > ...
