N！中末尾有多少个0

问题：先从100！的末尾有多少零         =>    再推广到  任意N！的末尾有多少个零

分析：首先想到慢慢求解出100！或N！，但计算机表示数有限，且要防止溢出。

则从数学上分析：一个整数若含有一个因子5则必然会在求100！时产生一个零，
                               问题转化为：求1到100，这100个整数中包含了多少个因子5.
                                若整数N能被25整除，则N包含2个因子5，若N能被5整除，则N包含1个因子5

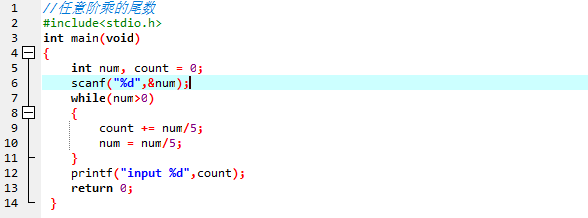
#include<stdio.h>
int main()
{
 int a,count = 0;
 for(a = 5;a <= 100;a+=5){
 count++;
 if(!(a%25)) count++;
    }
    printf("The number of 0 in the end of 100! i s:%d.\n",count);
    return 0;
 }

任意N！ ：对任意N质因数分解 N=2^x*3^Y*5^Z...

已知2*5=10，产生一个0.则min（x，y），实际上x存在量大于y，

则根据公式z = N/5+N/5^2+...+N/5^K