[Splay][学习笔记]

胡扯

因为先学习的treap，而splay与treap中有许多共性，所以会有很多地方不会讲的很细致。关于treap和平衡树可以参考这篇博客

关于splay

splay,又叫伸展树，是一种二叉排序树，它能在O(log n)内完成插入、查找和删除操作。它由Daniel Sleator和Robert Tarjan创造。伸展树是一种自调整形式的二叉查找树，它会沿着从某个节点到树根之间的路径，通过一系列的旋转把这个节点搬移到树根去。

splay与其他平衡树相比功能更加强大，可以处理区间问题。可以说其他平衡树可以做的splay几乎都能做。所以很多大佬都说平衡树会写splay就好了。唯一的缺点可能就是常数要比treap大。

定义

struct node {
    int ch[2],val,siz,cnt,pre;
}TR[N];

ch[0/1]分别为当前节点的两个儿子。val为当前节点的值。siz为以当前节点为根的子树大小，cnt为当前节点的值出现的次数。pre为当前节点的父亲节点

旋转

splay也是通过旋转来保持平衡的。spaly的旋转也是挺易懂的

如图，现在我们把4旋转到2这个位置。也就是说要把4号节点旋转上去。



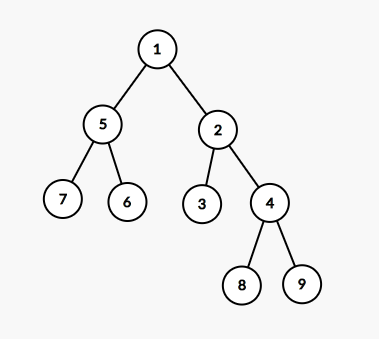
第一步：将2-4这条边断开，将8变为2的右儿子。



第二步：将1-2这条边断开，将4变为1的右儿子。



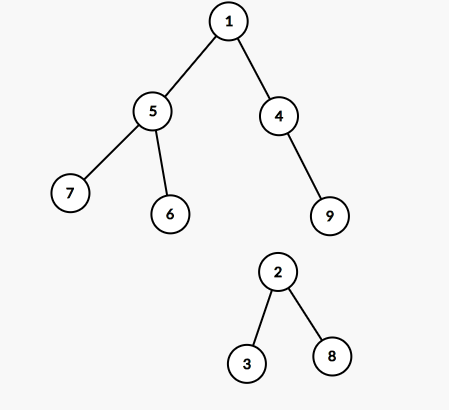
第三步：将2变为4的左儿子



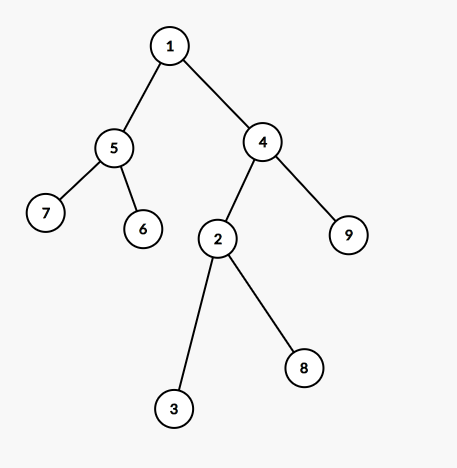
第四步：更新4号节点和2号节点，完成旋转

void rotate(int cur) {
    int f = getwh(cur),fa = TR[cur].pre,gr = TR[fa].pre;
    TR[gr].ch[getwh(fa)] = cur;
    TR[cur].pre = gr;
    TR[fa].ch[f] = TR[cur].ch[f ^ 1];
    TR[TR[cur].ch[f ^ 1]].pre = fa;
    TR[fa].pre = cur;
    TR[cur].ch[f ^ 1] = fa;
    up(fa);
    up(cur);
}

其中getwh是用来得到当前点是其父亲的左儿子还是右儿子，fa是当前点的父亲，gr是当前点的爷爷

getwh代码如下

int getwh(int cur) {
    return TR[TR[cur].pre].ch[1] == cur;
}

伸展

与treap相比，splay多了一种非常重要的操作——伸展操作。

所谓伸展，就是通过一系列旋转，将一个节点挪到一个想让他到达的位置(这个位置一般为根)。

splay的伸展总共可以分为三种情况(伸展到底有什么用后面会提到，现在只需知道他的作用如上即可)。

第一种情况：



如图，x结点要挪到他的爷爷结点下面，这种情况只要将x点旋转一次即可

第二种情况

x结点要挪到他爷爷的节点以上的节点下面，并且他的爷爷，和他的父亲，和他在同一直线上。

啥叫在同一直线上？？？



如图，现在g，p，x就在同一直线上，然后要将x转到右面的情况，只要现将p旋转上去，然后再讲x旋转上去即可

第三种情况，

x结点要挪到他爷爷的节点以上的节点下面，并且他的爷爷，和他的父亲，和他不在同一直线上。



如图，现在只要先将x旋转到p的位置，然后再将x旋转到g的位置即可

PS

经博主实践证明，第二和第三种情况都可以通过第三种情况的操作方式进行，至于为什么第二类不如此操作，大概是为了保持树的平衡。但是反而更慢

综上所述

我们可以得到伸展的代码(to为0时就是旋转成根)

void splay(int cur,int to) {
    while(TR[cur].pre != to) {
        if(TR[TR[cur].pre].pre != to) {
             if(getwh(cur) == getwh(TR[cur].pre)) rotate(TR[cur].pre);
             else rotate(cur);
        }
        rotate(cur);
    }
    if(!to) rt = cur;
}

插入

splay的插入和treap的插入类似。就是不断地寻找当前点恰当的位置，如果以前已经有了，就将cnt++即可，否则新建一个节点。

最后不要忘记将新插入的节点伸展为根。

void insert(int cur,int val,int lst) {
    if(!cur) {
        cur = ++tot;
        TR[cur].pre = lst;
        TR[cur].siz = TR[cur].cnt = 1;
        TR[cur].val = val;
        TR[lst].ch[val > TR[lst].val] = cur;
        splay(cur,0);
        return;
    }
    TR[cur].siz++;
    if(val == TR[cur].val) {TR[cur].cnt++;return;}
    if(val > TR[cur].val) insert(rs,val,cur);
    else insert(ls,val,cur);
}

合并

合并操作也是treap种所没有了。splay中的合并主要是为了删除操作做准备

所谓合并也就是将两棵子树合成一棵。两棵子树能合并的前提是其中一个中的所有元素大于另一棵的所有元素。

其实很简单，假如说现在x子树中的所有元素都小于y子树中的所有元素，那么只需找到x种最靠右的(也就是最大的)节点，然后将y变为此节点的右孩子即可。

最后还是要把y节点或者是x子树中最大的那个节点伸展为根。

void merge(int cur,int y) {
    if(TR[cur].val > TR[y].val) swap(cur,y);
    if(!cur) {
        rt = y;
        return;
    }
    while(rs) cur = rs;
    splay(cur,0);
    rs = y;
    TR[y].pre = cur;
    up(cur);
}

查找节点

这也是一个用来辅助其他操作的操作。作用是查找权值为val的节点。

很简单，就是在二叉搜索树上查找操作，如果比当前节点大就去查右子树，否则查左子树。和当前节点一样大了就范围即可。

int getpos(int cur,int val) {
    int lst;
    while(cur) {
        lst = cur;
        if(TR[cur].val == val) return cur;
        cur = TR[cur].ch[val > TR[cur].val];
    }
    return lst;
}

删除

有了合并操作，删除就很好完成了。首先找到要删除的节点，然后将此节点伸展为根。然后将这个节点的左右子树合并即可。

void del(int cur,int val) {
    cur = getpos(rt,val);
    if(!cur) return;
    if(TR[cur].val != val) return;
    splay(cur,0);
    if(TR[cur].cnt > 1) {TR[cur].cnt--;TR[cur].siz--;return;}
    TR[ls].pre = TR[rs].pre = 0;
    merge(ls,rs);
}

查询排名

用查找操作找到当前节点，然后旋转为根，左子树的大小+1就是这个节点的排名

查询第k大

与treap一样，如果k大于左子树大小+当前节点个数，就在右子树中查找k-左子树大小-当前节点个数。如果k<=左子树大小，那么直接在左子树中查找第k大。否则返回当前点即可。

int kth(int cur,int x) {
    while(cur) {
        if(x <= TR[ls].siz) cur = ls;
        else if(x > TR[ls].siz + TR[cur].cnt) x -= TR[cur].cnt + TR[ls].siz,cur = rs;
        else return TR[cur].val;
    }
    return cur;
}

前驱

找到要查询的点伸展为根。然后在左子树中查找最大值即可。

int pred(int cur,int val) {
    cur = getpos(rt,val);
    if(TR[cur].val < val) return TR[cur].val;
    splay(cur,0);
    cur = ls;
    while(rs) cur = rs;
    return TR[cur].val;
}

后继

找到要查询的点伸展为根。然后在右子树中查找最小值即可。

int nex(int cur,int val) {
    cur = getpos(rt,val);
    if(TR[cur].val > val) return TR[cur].val;
    splay(cur,0);
    cur = rs;
    while(ls) cur = ls;
    return TR[cur].val;
}

区间操作

关于splay的区间操作，可以参考这篇博客

完整代码

#include<cstdio>
#include<iostream>
using namespace std;
typedef long long ll;
const int N = 100000 + 100;
#define ls TR[cur].ch[0]
#define rs TR[cur].ch[1]
ll read() {
    ll x = 0,f = 1;char c = getchar();
    while(c < '0' || c > '9') {
        if(c == '-') f = -1;
        c = getchar();
    }
    while(c >= '0' && c <= '9') {
        x = x * 10 + c -'0';
        c = getchar();
    }
    return x * f;
}
int rt;
struct node {
    int ch[2],val,siz,cnt,pre;
}TR[N];
void up(int cur) {
    TR[cur].siz = TR[ls].siz + TR[rs].siz + TR[cur].cnt;
}
int getwh(int cur) {
    return TR[TR[cur].pre].ch[1] == cur;
}
void rotate(int cur) {
    int f = getwh(cur),fa = TR[cur].pre,gr = TR[fa].pre;
    TR[gr].ch[getwh(fa)] = cur;
    TR[cur].pre = gr;
    TR[fa].ch[f] = TR[cur].ch[f ^ 1];
    TR[TR[cur].ch[f ^ 1]].pre = fa;
    TR[fa].pre = cur;
    TR[cur].ch[f ^ 1] = fa;
    up(fa);
    up(cur);
}
void splay(int cur,int to) {
    while(TR[cur].pre != to) {
        if(TR[TR[cur].pre].pre != to) {
            // if(getwh(cur) == getwh(TR[cur].pre)) rotate(TR[cur].pre);
            // else
                rotate(cur);
        }
        rotate(cur);
    }
    if(!to) rt = cur;
}
int tot;
void insert(int cur,int val,int lst) {
    if(!cur) {
        cur = ++tot;
        TR[cur].pre = lst;
        TR[cur].siz = TR[cur].cnt = 1;
        TR[cur].val = val;
        TR[lst].ch[val > TR[lst].val] = cur;
        splay(cur,0);
        return;
    }
    TR[cur].siz++;
    if(val == TR[cur].val) {TR[cur].cnt++;return;}
    if(val > TR[cur].val) insert(rs,val,cur);
    else insert(ls,val,cur);
}
void merge(int cur,int y) {
    if(TR[cur].val > TR[y].val) swap(cur,y);
    if(!cur) {
        rt = y;
        return;
    }
    while(rs) cur = rs;
    splay(cur,0);
    rs = y;
    TR[y].pre = cur;
    up(cur);
}
int getpos(int cur,int val) {
    int lst;
    while(cur) {
        lst = cur;
        if(TR[cur].val == val) return cur;
        cur = TR[cur].ch[val > TR[cur].val];
    }
    return lst;
}
void del(int cur,int val) {
    cur = getpos(rt,val);
    if(!cur) return;
    if(TR[cur].val != val) return;
    splay(cur,0);
    if(TR[cur].cnt > 1) {TR[cur].cnt--;TR[cur].siz--;return;}
    TR[ls].pre = TR[rs].pre = 0;
    merge(ls,rs);
}
int Rank(int cur,int val) {
    cur = getpos(rt,val);
    splay(cur,0);
    return TR[ls].siz + 1;
}
int kth(int cur,int x) {
    while(cur) {
        if(x <= TR[ls].siz) cur = ls;
        else if(x > TR[ls].siz + TR[cur].cnt) x -= TR[cur].cnt + TR[ls].siz,cur = rs;
        else return TR[cur].val;
    }
    return cur;
}
int pred(int cur,int val) {
    cur = getpos(rt,val);
    if(TR[cur].val < val) return TR[cur].val;
    splay(cur,0);
    cur = ls;
    while(rs) cur = rs;
    return TR[cur].val;
}
int nex(int cur,int val) {
    cur = getpos(rt,val);
    if(TR[cur].val > val) return TR[cur].val;
    splay(cur,0);
    cur = rs;
    while(ls) cur = ls;
    return TR[cur].val;
}
int main() {
    int n = read();
    while(n--) {
        int opt = read(),x = read();
        if(opt == 1) insert(rt,x,0);
        if(opt == 2) del(rt,x);
        if(opt == 3) printf("%d\n",Rank(rt,x));
        if(opt == 4) printf("%d\n",kth(rt,x));
        if(opt == 5) printf("%d\n",pred(rt,x));
        if(opt == 6) printf("%d\n",nex(rt,x));
    }
    return 0;
}