CF1101F Trucks and Cities

题意：给定线段上n个特殊点，m次询问。

每次询问：在第l个点到第r个点这一段区间中选出k个点，将其分成k + 1段。使得最长的段尽量短。

输出这m个询问中答案最大的。 n<=400,m<=250000

解：显然有个暴力DP是n⁴的。f[l][r][k]表示把[l, r]分成k段的最短长度。

然后我们发现一件事：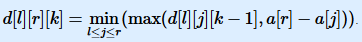

考虑j增加的时候，这个东西左半边单增，右半边单减。于是这个东西对于j是个凸的。

还发现r增大的时候，j一定不会减少。

然后枚举l和k，r递增的同时让一个指针j跟着增加。这样就是n³DP了。

 #include <bits/stdc++.h>

 typedef long long LL;
 const int N = ;

 int f[N][N][N], a[N];

 int main() {
     int n, m;
     scanf("%d%d", &n, &m);
     for(int i = ; i <= n; i++) {
         scanf("%d", &a[i]);
     }

     for(int l = ; l <= n; l++) {
         for(int r = l; r <= n; r++) {
             f[l][r][] = a[r] - a[l];
         }
     }

     for(int l = ; l < n; l++) {
         for(int k = ; k <= n; k++) {
             int p = l + ;
             for(int r = l + ; r <= n; r++) {
                 while(p < r -  && std::max(f[l][p][k - ], a[r] - a[p]) >= std::max(f[l][p + ][k - ], a[r] - a[p + ])) {
                     p++;
                 }
                 f[l][r][k] = std::max(f[l][p][k - ], a[r] - a[p]);
             }
         }
     }

     LL ans = ;
     for(int i = , l, r, c, k; i <= m; i++) {
         scanf("%d%d%d%d", &l, &r, &c, &k);
         ans = std::max(ans, 1ll * c * f[l][r][k]);
     }
     printf("%lld\n", ans);
     return ;
 }

AC代码

空间刚好卡着。要卡空间的话就离线 + 滚动数组滚掉l。