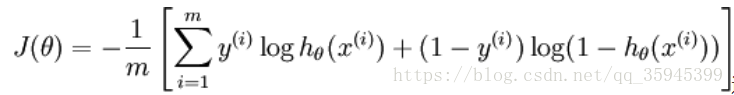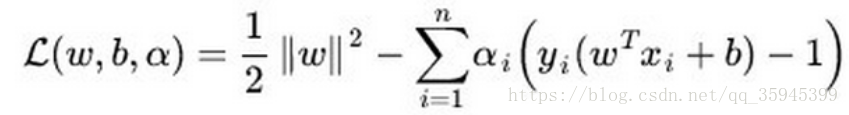机器学习理论基础学习3.3--- Linear classification 线性分类之logistic regression（基于经验风险最小化）

一、逻辑回归是什么？

1、逻辑回归

逻辑回归假设数据服从伯努利分布,通过极大化似然函数的方法，运用梯度下降来求解参数，来达到将数据二分类的目的。

logistic回归也称为逻辑回归，与线性回归这样输出是连续的、具体的值（如具体房价123万元）不同，逻辑回归的输出是0~1之间的概率，但可以把它理解成回答“是”或者“否”（即离散的二分类）的问题。回答“是”可以用标签“1”表示，回答“否”可以用标签“0”表示。
比如，逻辑回归的输出是“某人生病的概率是多少”，我们可以进一步理解成“某人是否生病了”。设置一个阈值如0.5，如果输出的是“某人生病的概率是0.2”，那么我们可以判断“此人没有生病”（贴上标签“0”）。

（1）基本假设

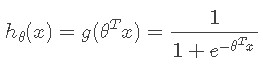其中

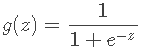
这个g(z)函数被称为逻辑函数（Logistic function）或者是S形函数（Sigmoid function），它是由伯努利分布通过广义线性模型求解得到的，不是凭空捏造的。下面是它的函数图像：

可以看到z在0附近比较敏感，当z>>0时它的输出很接近1，当z<<0时它的输出很接近0。这样我们在确定参数θ之后，就可以对新到来的数据进行预测（分类）了。 
同时直接给出其求导结果：

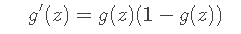
（2）损失函数

逻辑回归的损失函数是它的极大似然函数

（3）求解方法

由于该极大似然函数无法直接求解，我们一般通过对该函数进行梯度下降来不断逼急最优解。因为就梯度下降本身来看的话就有随机梯度下降，批梯度下降，small batch 梯度下降三种方式：

• 简单来说 批梯度下降会获得全局最优解，缺点是在更新每个参数的时候需要遍历所有的数据，计算量会很大，并且会有很多的冗余计算，导致的结果是当数据量大的时候，每个参数的更新都会很慢。
• 随机梯度下降是以高方差频繁更新，优点是使得sgd会跳到新的和潜在更好的局部最优解，缺点是使得收敛到局部最优解的过程更加的复杂。
• 小批量梯度下降结合了sgd和batch gd的优点，每次更新的时候使用n个样本。减少了参数更新的次数，可以达到更加稳定收敛结果，一般在深度学习当中我们采用这种方法。

Adam，动量法等优化方法

• 第一个是如何对模型选择合适的学习率。自始至终保持同样的学习率其实不太合适。因为一开始参数刚刚开始学习的时候，此时的参数和最优解隔的比较远，需要保持一个较大的学习率尽快逼近最优解。但是学习到后面的时候，参数和最优解已经隔的比较近了，你还保持最初的学习率，容易越过最优点，在最优点附近来回振荡，通俗一点说，就很容易学过头了，跑偏了。
• 第二个是如何对参数选择合适的学习率。在实践中，对每个参数都保持的同样的学习率也是很不合理的。有些参数更新频繁，那么学习率可以适当小一点。有些参数更新缓慢，那么学习率就应该大一点。

2、几个问题

（1）LR为什么使用sigmoid函数作为激活函数？其他函数不行吗？

答：因为作为广义线性模型（GLM）中的一类，逻辑回归的连接函数的 canonical 形式就是 sigmoid函数（具体解释看这里）

（2）LR为什么要使用极大似然函数作为损失函数？

损失函数一般有四种，平方损失函数，对数损失函数，HingeLoss0-1损失函数，绝对值损失函数。将极大似然函数取对数以后等同于对数损失函数。在逻辑回归这个模型下，对数损失函数的训练求解参数的速度是比较快的。至于原因大家可以求出这个式子的梯度更新

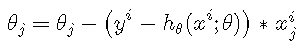
这个式子的更新速度只和xij，yi相关。和sigmod函数本身的梯度是无关的。这样更新的速度是可以自始至终都比较的稳定。

那为什么不选平方损失函数的呢？

其一是因为如果你使用平方损失函数，你会发现梯度更新的速度和sigmod函数本身的梯度是很相关的。sigmod函数在它在定义域内的梯度都不大于0.25。这样训练会非常的慢。

（3）逻辑回归在训练的过程当中，如果有很多的特征高度相关或者说有一个特征重复了100遍，会造成怎样的影响？

• 先说结论，如果在损失函数最终收敛的情况下，其实就算有很多特征高度相关也不会影响分类器的效果。
• 但是对特征本身来说的话，假设只有一个特征，在不考虑采样的情况下，你现在将它重复100遍。训练以后完以后，数据还是这么多，但是这个特征本身重复了100遍，实质上将原来的特征分成了100份，每一个特征都是原来特征权重值的百分之一。
• 如果在随机采样的情况下，其实训练收敛完以后，还是可以认为这100个特征和原来那一个特征扮演的效果一样，只是可能中间很多特征的值正负相消了。

（4）为什么我们还是会在训练的过程当中将高度相关的特征去掉？

• 去掉高度相关的特征会让模型的可解释性更好
• 可以大大提高训练的速度。如果模型当中有很多特征高度相关的话，就算损失函数本身收敛了，但实际上参数是没有收敛的，这样会拉低训练的速度。其次是特征多了，本身就会增大训练的时间。

二、怎么确定逻辑回归的参数？

到了这里，怎么才能得到参数θ？
其实这跟求解线性回归问题是同样的套路，前后改变了的地方只有P不同，而概率P不一样是因为模型不一样（一个高斯分布一个两点分布），所以计算概率的方式也不一样，前后求解的思路都是一样的。就连具体处理方式都是类似的梯度法，就像线性回归是让你计算29+3629+36，逻辑回归是让你计算57+2857+28，同样是计算一个加法算式，区别只在具体相加的数字的变化，没有本质的不同。
线性回归中用概率解释了最小二乘成本函数的由来，这里也用概率来得出我们要优化的目标函数，然后通过最大似然估计来求解θ。
让我们做出如下假设，这实际上是一个伯努利分布（Bernoulli distribution），也称为两点分布

这两个式子可以写在一起：

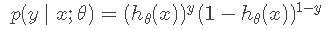
有了概率我们就能得到似然函数，并且为了计算方便这里同样取log：

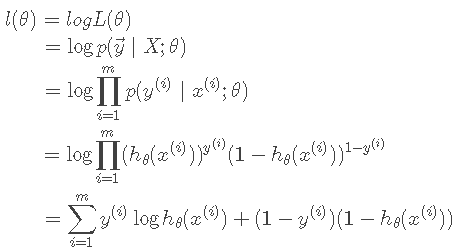
这里，我们就有了目标函数l(θ)即J(θ)，当它的概率最大的时候，其对应的θ就是我们所寻求的参数。

具体求解方法：梯度上升（Gradient ascent）

在线性回归中，我们对J(θ)提出了两种解法，一种是梯度下降，另一种是正规方程组。

类似地，我们这里使用梯度上升，迭代规则为

　　

注意这里是加号不是减号。

为什么上面用梯度下降这里用梯度上升？因为线性回归中它最大化的目标项之前有一个负号，为了把这个负号去掉，转而去求没有负号的目标项的最小值，故而采用了梯度下降，在逻辑回归中没有负号的问题，就使用了梯度上升。它们的本质都是在使似然函数l(θ)最大化。

下面直接给出一个样本下求导后的结果：

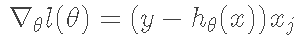
相应的迭代规则就是：

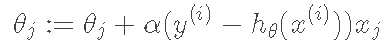
三、逻辑回归的特点及优缺点

（1）特点

1)可用于概率预测，也可用于分类。 
并不是所有的机器学习方法都可以做可能性概率预测（比如SVM就不行，它只能得到1或者-1）。可能性预测的好处是结果又可比性：比如我们得到不同广告被点击的可能性后，就可以展现点击可能性最大的N个。这样以来，哪怕得到的可能性都很高，或者可能性都很低，我们都能取最优的topN。当用于分类问题时，仅需要设定一个阈值即可，可能性高于阈值是一类，低于阈值是另一类。 
2)仅能用于线性问题 
只有在feature和target是线性关系时，才能用Logistic Regression（不像SVM那样可以应对非线性问题）。这有两点指导意义，一方面当预先知道模型非线性时，果断不使用Logistic Regression； 另一方面，在使用Logistic Regression时注意选择和target呈线性关系的feature。 
3)各feature之间不需要满足条件独立假设，但各个feature的贡献是独立计算的。 
逻辑回归不像朴素贝叶斯一样需要满足条件独立假设（因为它没有求后验概率）。但每个feature的贡献是独立计算的，即LR是不会自动帮你combine 不同的features产生新feature的 (时刻不能抱有这种幻想，那是决策树,LSA, pLSA, LDA或者你自己要干的事情)。举个例子，如果你需要TF*IDF这样的feature，就必须明确的给出来，若仅仅分别给出两维 TF 和 IDF 是不够的，那样只会得到类似 a*TF + b*IDF 的结果，而不会有 c*TF*IDF 的效果。

4)LR对于样本噪声是robust的;

5)对缺失数据敏感；

6)可用于在线学习；

（2）优缺点

优点：

• 形式简单，模型的可解释性非常好。从特征的权重可以看到不同的特征对最后结果的影响，某个特征的权重值比较高，那么这个特征最后对结果的影响会比较大。

• 模型效果不错。在工程上是可以接受的（作为baseline)，如果特征工程做的好，效果不会太差，并且特征工程可以大家并行开发，大大加快开发的速度。

• 训练速度较快。分类的时候，计算量仅仅只和特征的数目相关。并且逻辑回归的分布式优化sgd发展比较成熟，训练的速度可以通过堆机器进一步提高，这样我们可以在短时间内迭代好几个版本的模型。

• 资源占用小,尤其是内存。因为只需要存储各个维度的特征值，。

• 方便输出结果调整。逻辑回归可以很方便的得到最后的分类结果，因为输出的是每个样本的概率分数，我们可以很容易的对这些概率分数进行cutoff，也就是划分阈值(大于某个阈值的是一类，小于某个阈值的是一类)。

缺点：

• 准确率并不是很高。因为形式非常的简单(非常类似线性模型)，很难去拟合数据的真实分布。

• 很难处理数据不平衡的问题。举个例子：如果我们对于一个正负样本非常不平衡的问题比如正负样本比 10000:1.我们把所有样本都预测为正也能使损失函数的值比较小。但是作为一个分类器，它对正负样本的区分能力不会很好。

• 处理非线性数据较麻烦。逻辑回归在不引入其他方法的情况下，只能处理线性可分的数据，或者进一步说，处理二分类的问题 。

• 逻辑回归本身无法筛选特征。有时候，我们会用gbdt来筛选特征，然后再上逻辑回归。

四、逻辑回归与线性回归、SVM有什么异同？

1、LR与线性回归的区别：

逻辑回归用的是对数似然(或称交叉熵)，而线性回归用的是平方误差。这是因为逻辑回归是二项分布，而线性回归是高斯分布，因此用不同的cost function。另外一个比较明显的区别是逻辑回归对线性变换的结果用了sigmoid函数，使得结果映射到(0,1)的区间，但大多数时候我们仍然称它为线性分类器。

2、LR与SVM的不同点

1、本质上是loss函数不同，或者说分类的原理不同。

LR的目标是最小化模型分布和经验分布之间的交叉熵：

　　

LR基于概率理论中的极大似然估计。首先假设样本为0或者1的概率可以用sigmoid函数来表示，然后通过极大似然估计的方法估计出参数的值，即让模型产生的分布P(Y|X)尽可能接近训练数据的分布。

SVM的目标是最大化分类间隔（硬SVM），或者最大化 [分类间隔—a*分错的样本数量]（软SVM）

　　
SVM​基于几何间隔最大化原理，认为几何间隔最大的分类面为最优分类面 。

2、SVM是结构风险最小化，LR则是经验风险最小化。

结构风险最小化就是在训练误差和模型复杂度之间寻求平衡，防止过拟合，减小泛化误差。为了达到结构风险最小化的目的，最常用的方法就是添加正则项。

SVM的loss函数的第一项可看作L2正则项；LR需要加入正则化项。

3、SVM只考虑分界面附近的少数点，而LR则考虑所有点。

影响SVM决策面的样本点只有少数的支持向量。在支持向量外添加或减少任何样本点，对分类决策面没有任何影响。

在LR中，每个样本点都会影响决策面。决策面会倾向于远离样本数量较多的类别。如果不同类别之间的数量严重不平衡，一般需要先对数据做balancing。

4、SVM不能产生概率，LR可以产生概率。

5、在解决非线性问题时，SVM可采用核函数的机制，而LR通常不采用核函数的方法。

SVM只有少数几个样本需要参与核计算（即kernal machine解的系数是稀疏的）。

LR里每个样本点都要参与核计算，计算复杂度太高，故LR通常不用核函数。

6、SVM计算复杂，但效果比LR好，适合小数据集；LR计算简单，适合大数据集，可以在线训练。

参考文献：

【1】逻辑回归的常见面试点总结