Andrew Ng-ML-第十六章-异常检测

1.问题动机

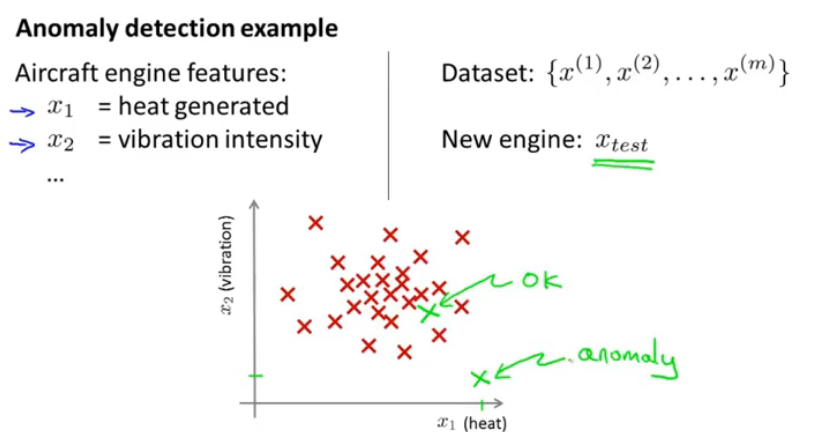
图1.飞机发动机检测例子

对飞机引擎的例子，如果选取了两个特征x1热量产生度，x2震动强度。并得到如下的图，如果有一个新的引擎来检测其是否正常，x_test，那么此时如果点落在和其他点正常内，那么就显示是正常，不需要进一步的检测，但是如果在右下角绿色的，那么就是异常的，需要进一步地检测。

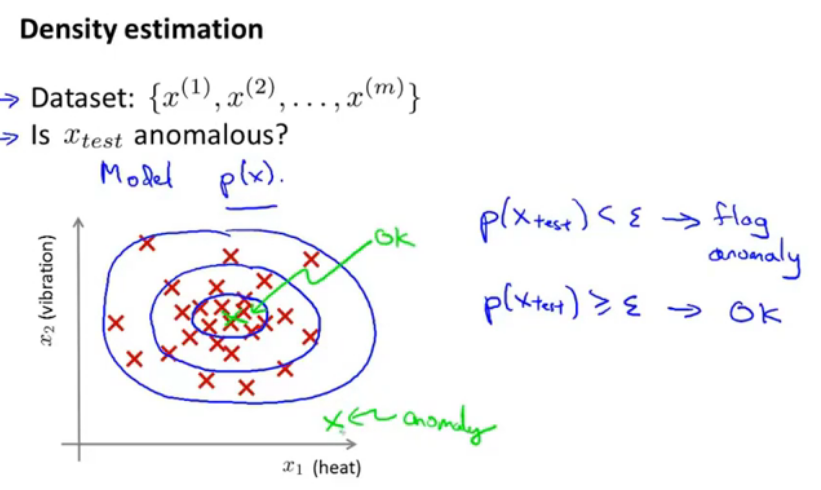
图1.密度检测

更一般地建立模型，当x_test输入时，若概率<阈值ε，那么就被设置为异常；否则设置为正常。如图来看，中心部分的概率大，四周部分概率小。

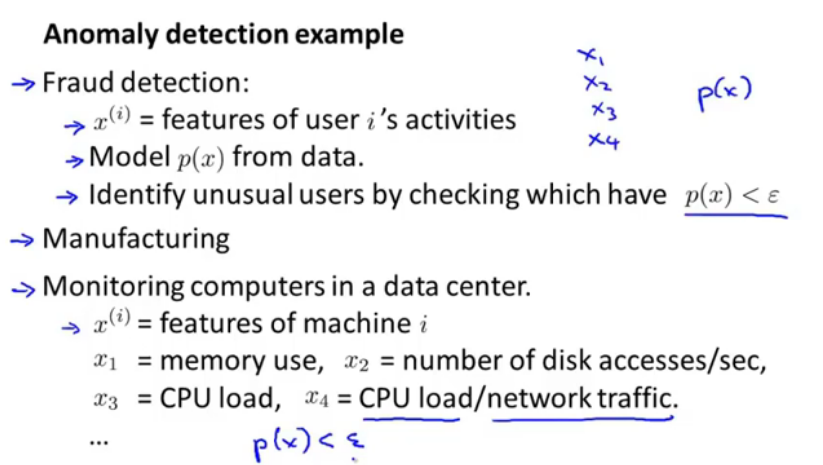
图2.异常检测的应用

异常检测最常见的应用是进行，用户欺诈检测，对用户的模型作为向量，从数据中建立模型，异常用户为:p(x)<ε。还有在工业生产，检测计算机中心。

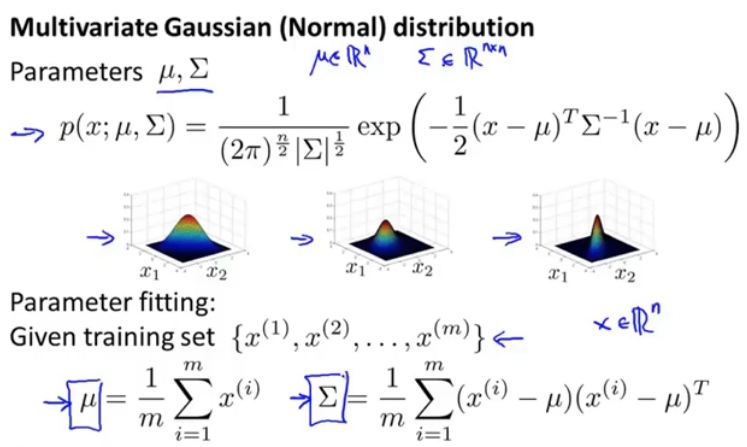
2.高斯分布/正态分布

其中μ是均值，σ是方差，可以使用公式来计算。曲线特点：当σ越小时，曲线越瘦高；当σ越大时，曲线越胖矮。并且根据概率的性质，曲线下方面积为1。

3.算法

图3.密度估计问题

对一个无标记的训练集来说，建立的模型为如上式，是一个独立假设问题，假设x_i均服从正态分布并且使独立的，那么p(x)就是这个密度估计模型，写成了阶乘的形式。（也是符合高斯分布的，当其处于均值附近，那么p就对应比较大，是符合刚刚讲的检测结果，如果p(x)<σ，那么就是异常的，不符合大部分点的分布。）

图4.异常检测算法

这就是所谓的异常检测算法，不就是求训练集的高斯分布参数，有新的样本来时，观察其是否分布在均值附近了。最终结果，如果p(x)<σ，那么就是异常的。

注意：这里不是对一个向量x,而是针对向量中每个分量，即每个特征值！，都有那么一个高斯分布，并且整个样本的决定是通过连乘。

4.开发和评估异常检测系统

图5.数值评估的重要性

当进行一个学习算法时，当有一个方法来进行评估，那么此时是更容易决策的。

假设现在有一些标记数据，y=1表示是异常的，在训练集中假设全都是正常样本，不包括异常样本，并且有验证集和训练集。

图6.发动机引擎例子

假设数据集一共包括10000个正常引擎数据和20个一场引擎数据，好的数据集分法是：

训练集中有6000个正常引擎数据，交叉验证集中2000个正常，10个异常，测试集中2000个正常，10个异常。通常交叉验证机和测试集的数据是不一样的，也不应该是一样的。

下一种分法是不好的分法，但通常有人这么做，就是将交叉验证集和测试集中的数据完全一样，这是不可取的。

图7.算法评估

通过在训练集上训练出模型，当p(x)<ε时被判断为异常点，反正则正常；

那么如何去评估这个算法呢？由于这个问题数据集明显是偏斜的，所以使用以下:

查准率和查全率，F_1公式；

或者也可以使用在交叉验证集上设置阈值ε来计算，这个和公式判断异常或正常中的ε是相同的。通过设置很多ε，并且在交叉验证集上测试，并选取一个让F_1公式最高的ε。（并且使用这个来决策，也可以决定哪个特征应该被选择，哪个不被选择。）

5.异常检测VS监督学习

那么既然对于有标签的数据，为什么使用异常检测而不是直接训练一个监督学习的模型呢？

图8.异常检测与监督学习

异常检测的数据集特征：通常都是负例，只有很少的部分是正例（0-20是比较常见的）。

有很多种不同类型的异常，并且很难从正例中去找出算法来学习其特征（比如飞机发动机引擎出故障的原因），并且下次出现的异常很有可能从来没见过。

 监督学习的数据集特征：有大量的正例和负例。

能够有足够多的正例去让算法获取特征，将来出来的样例可能和之前在训练集中出现的类似。

比如对于垃圾邮件分类，虽然很有可能下一次出现的并不和之前训练集中相同，但是因为可以获取足够多的垃圾邮件的数据，所以通常使用监督学习的方法来进行垃圾邮件分类。

图9.问题应用

对于异常检测：缺陷检测、工业生产、数据中心监督机器。（关键点是这些缺陷点的数据够不够多，比如在工业生产中，如果缺陷数据够多，那么也可也建立监督模型。）

监督学习：垃圾邮件分类、天气预测、癌症分类。

6.选择要使用的特征

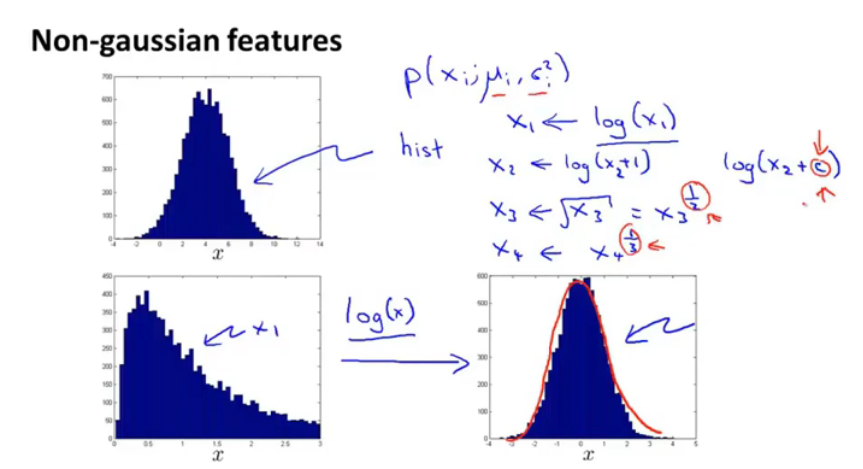
图10.不是高斯分布的特征

图中1是很类似于高斯分布的，所以这样的特征是很乐意加进来的，但是像图中2，就需要进行一下转换来使其尽量符合高斯分布。

比如：取logx、或者log(x+c)、取根号。

图中红圈标出来的均是可调整参数，都是为了让特征数据分布更趋近于高斯分布。

关于异常算法的误差检测，如果表现不好，那么就考虑那个未能正常分类的异常数据，去观察它，并且判断能否新建一个特征x_2来区别这个异常数据以改进算法。

那么如何进行特征选择呢？

图11.在数据中心的电脑检测例子

Ng会选择那些数值及不是很大，也不是很小的特征。

比如对x_3和x_4，分别表示CPU负载和网络流量，发现基本是线性关系，但是当发现网络流量上升很大时，CPU却上升不明显，是因为CPU做了很多工作卡死了。

在这种情况下，要想检测出异常，就可以新建一个特征x_5或者x_6.

7.多变量高斯分布

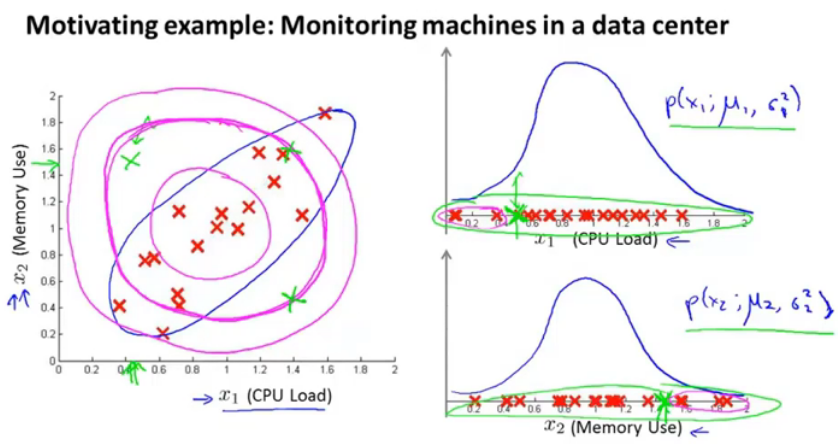
图12.单变量高斯分布判断存在隐患

如果有一个点是图中1左上角的绿色点，那么从图中1来看其是异常点，但是对应对每个特征建模的高斯分布，每个分布的P都比较高，所以最终得出的乘积也比较高，因此就出现了问题。单个变量进行高斯分布建模，不好。

第二层洋红色圈即表示，出现在这一范围内很大可能被表示为正常数据。

所以接下来介绍多变量高斯分布建模，避免类似的问题出现。

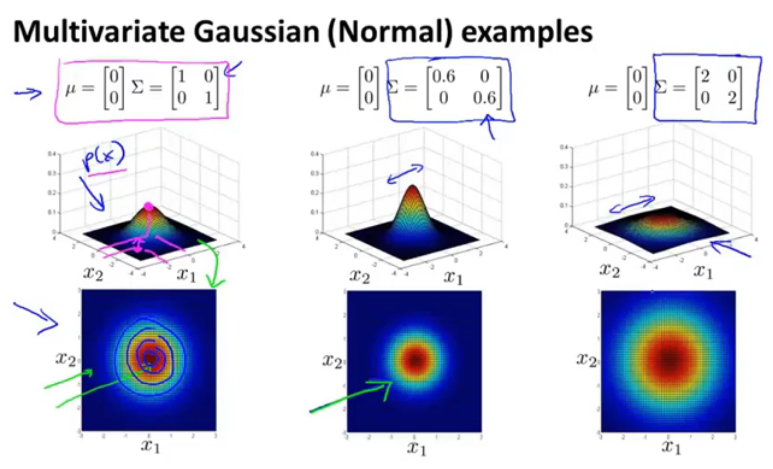
图13.多变量高斯分布可视化

这里的Σ矩阵就相当于方差，它的行列式即方差，那么和一维的是类似的。

当Σ较小时，较高瘦；当Σ较大时，较胖矮。

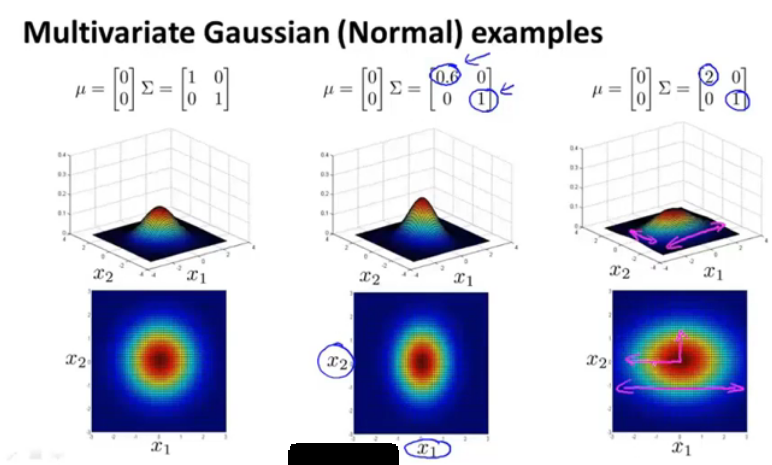
图14.Σ矩阵变化的影响

对于协方差矩阵Σ的行列式，对图中2，当第一行的方方差减小时，明显图中x_1对应的是在变小。

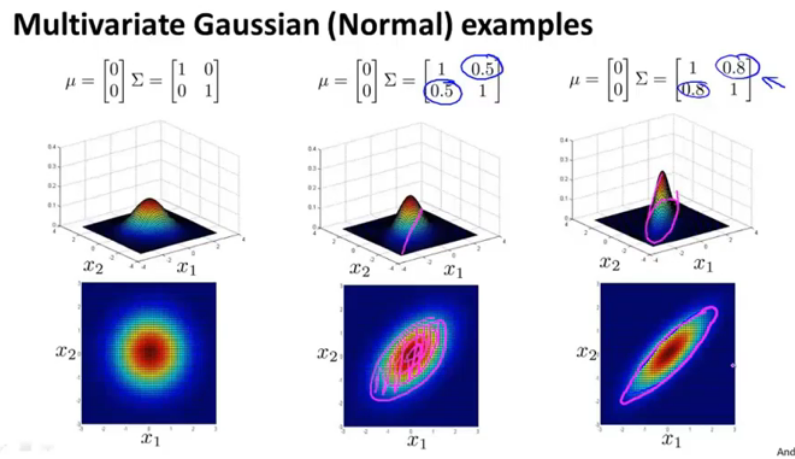
图15.多变量高斯分布的例子

当改变Σ行列式的非对角线上的元素时，对应的形状也会发生改变，这样就对应了开头的例子，可以解决对应的问题，

8.使用多变量高斯分布的异常检测

图16.多变量高斯分布公式

当给出一个训练集时，可以计算出参数μ和Σ。（这里不是计算出每个特征对应的参数，而是每一个测试数据都是整个向量代入的。）

图17.多变量高斯分布模型

首先通过μ和协方差矩阵Σ，拟合出一个模型， 然后再给出一个新的样本，计算p(x)。

在图中，距离椭圆中心越近表示概率越高，反之绿色的点此时就会被判定为异常。

图18.多变量与原始模型的关系

原始的模型不能表示变量与变量之间的关系，而且它们的投影圆的对称轴都是与坐标轴垂直的。

而在多变量正态分布中，有协方差矩阵，但是当协方差矩阵为对角阵时，就会退化为原始模型（不能表示不同变量之间的关系了）。

原始模型只是高斯分布的一种特殊情况。

图19.原始模型VS多变量高斯模型

1.当你想通过特征的组合来判断异常时，比如之前举的例子中，x_3=x_1/x_2=CPU负载/内存，原始模型需要手动地去选择特征组合，

而多变量模型可以自动地表示特征与特征之间的关系，因为它有协方差矩阵了。监测到异常就将其标记。

2.原始模型适合n较大的时候，即n=100,000,之类，计算量较小；对于多变量来说，由于需要计算逆矩阵，计算量很大，对应于n较小的情况。

3.原始模型中对训练集m很小也是可以使用的；多变量中，需要满足两个条件m>n，m要大于n,比如说m>10n，并且必须是可逆的。

不可逆的情况是什么呢？需要用到线代，不可逆也就是|Σ|=0，协方差行列式=0，通过初等行列变换，可以让一行全为0，那么矩阵就是不可逆的，如x_1=x_2,x_3=x_4+x_5.这样的情况