hdu-1404-博弈+打表

Digital Deletions

Time Limit: 4000/2000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 3312    Accepted Submission(s): 1194

Problem Description

Digital deletions is a two-player game. The rule of the game is as following.

Begin by writing down a string of digits (numbers) that's as long or as short as you like. The digits can be 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 and appear in any combinations that you like. You don't have to use them all. Here is an example:

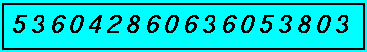
On a turn a player may either:
Change any one of the digits to a value less than the number that it is. (No negative numbers are allowed.) For example, you could change a 5 into a 4, 3, 2, 1, or 0. 
Erase a zero and all the digits to the right of it.

The player who removes the last digit wins.

The game that begins with the string of numbers above could proceed like this:

Now, given a initial string, try to determine can the first player win if the two players play optimally both.

 

Input

The input consists of several test cases. For each case, there is a string in one line.

The length of string will be in the range of [1,6]. The string contains only digit characters.

Proceed to the end of file.

 

Output

Output Yes in a line if the first player can win the game, otherwise output No.

 

Sample Input

0
00
1
20

 

Sample Output

Yes
Yes
No
No

 

Author

ZHENG, Jianqiang

 

Source

Zhejiang University Local Contest 2006 Preliminary

 

　　　　学的东西学不好总会干扰自己，一看到这个就想sg函数，，但是由于每个状态的子状态太多了，一一枚举的话不太现实。注意到这个游戏就是一个单独的游戏，不可利用sg定理分成多个子游戏，所以我们只要知道这个状态是0 or 1就好了，不必计算出所有的sg值= =，还是自己思维太固定了。

　　　这样的话可以利用必败态推出所有的必胜态，0表示lose，1表示win即可。

 #include<bits/stdc++.h>
 using namespace std;
 bool sg[];
 void dfs(int n,int l){
     if(l>) return;
     n=n*;
     for(int i=;i<=;++i){
         if(n+i>) break;
         sg[n+i]=;
         dfs(n+i,l+);
     }
 }
 void init(){
     sg[]=;
     sg[]=;
     for(int i=;i<=;++i){
         if(!sg[i]){
             int m=i,n=i,base=;
             while(n){
                 int q=-n%;
                 for(int j=;j<=q&&m+j*base<=;++j){
                     sg[m+j*base]=;
                     //if(i==233)cout<<m+j*base<<endl;
                 }
                 n/=;
                 base*=;
             }
             if(i<=){
                 int n=i*;
                 sg[n]=;
                 int l=log10(n+0.5)+;
                 dfs(n,l);
             }
         }
     }
 }
 int main(){
     char s[];
     init();
     while(scanf("%s",s)!=EOF){
         if(s[]==''){
             puts("Yes");
             continue;
         }
         int n=,len=strlen(s);
         for(int i=;i<len;++i)
             n=n*+(s[i]-'');
         sg[n]?puts("Yes"):puts("No");
     }
     return ;
 }