浅谈压缩感知（十四）：傅里叶矩阵与小波变换矩阵的MATLAB实现

主要内容：

1. 傅里叶矩阵及其MATLAB实现
2. 小波变换矩阵及其MATLAB实现 

傅里叶矩阵及其MATLAB实现

傅里叶矩阵的定义：（来源： http://mathworld.wolfram.com/FourierMatrix.html）

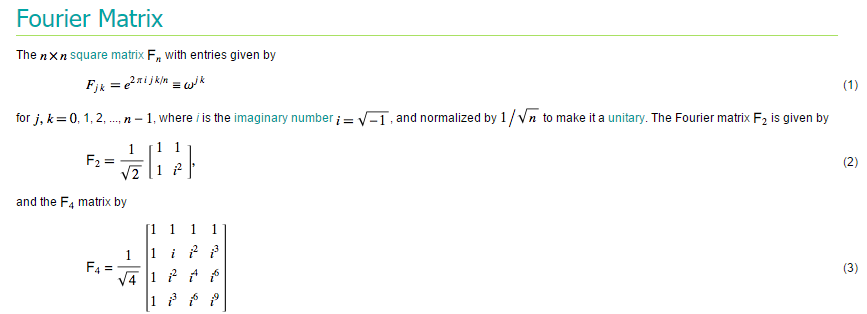
傅里叶矩阵的MATLAB实现：

　　dftmtx(N) is the N-by-N complex matrix of values around the unit-circle whose inner product with a column vector of length N yields the discrete Fourier transform of the vector. If X is a column vector of length N, then dftmtx(N)*X yields the same result as FFT(X); however, FFT(X) is more efficient.

　　The inverse discrete Fourier transform matrix is CONJ(dftmtx(N))/N.

% clc;clear;
N = ;
X = randn(N,);
dft_result1 = dftmtx(N)*X;
dft_result2 = fft(X);
% isEqual = all(dft_result1 == dft_result2);
err = norm(dft_result1(:)-dft_result2(:));
if err < 0.01
    fprintf('dftmtx(N)*X yields the same result as FFT(X)');
else
    fprintf('dftmtx(N)*X does not yield the same result as FFT(X)');
end

小波变换矩阵及其MATLAB实现

小波变换矩阵的概念：

参考：http://blog.csdn.net/jbb0523/article/details/42470103

小波变换矩阵的MATLAB实现：

function [ ww ] = dwtmtx( N,wtype,wlev )
%DWTMTX Discrete wavelet transform matrix
%   This function generates the transform matrix ww according to input
%   parameters N,wtype,wlev .
%Detailed explanation goes here
%   N is the dimension of ww
%   wtype is the wavelet type
%   wlev is the number of decomposition level
%NOTE: The extension mode must be Periodization('per')
[h,g]= wfilters(wtype,'d');         %Decomposition low&high pass filter
L=length(h);                        %Filter length
h_1 = fliplr(h);                    %Flip matrix left to right
g_1 = fliplr(g);
loop_max = log2(N);
loop_min = double(int8(log2(L)))+;
if wlev>loop_max-loop_min+
    fprintf('\nWaring: wlev is too big\n');
    fprintf('The biggest wlev is %d\n',loop_max-loop_min+);
    wlev = loop_max-loop_min+;
end
ww=;
for loop = loop_max-wlev+:loop_max
    Nii = ^loop;
    p1_0 = [h_1 zeros(,Nii-L)];
    p2_0 = [g_1 zeros(,Nii-L)];
    p1 = zeros(Nii/,Nii);
    p2 = zeros(Nii/,Nii);
    for ii=:Nii/
        p1(ii,:)=circshift(p1_0',2*(ii-1)+1-(L-1)+L/2-1)';
        p2(ii,:)=circshift(p2_0',2*(ii-1)+1-(L-1)+L/2-1)';
    end
    w1=[p1;p2];
    mm=^loop_max-length(w1);
    w=[w1,zeros(length(w1),mm);zeros(mm,length(w1)),eye(mm,mm)];
    ww=ww*w;
    clear p1;clear p2;
end

%The end!!!
end

验证是否与Matlab自带的函数wavedec所得结果一致：

%验证函数dwtmtx的正确性
clear all;close all;clc;
N = ^;
% 'db1' or 'haar', 'db2', ... ,'db10', ... , 'db45'
% 'coif1', ... , 'coif5'
% 'sym2', ... , 'sym8', ... ,'sym45'
% 'bior1.1', 'bior1.3', 'bior1.5'
% 'bior2.2', 'bior2.4', 'bior2.6', 'bior2.8'
% 'bior3.1', 'bior3.3', 'bior3.5', 'bior3.7'
% 'bior3.9', 'bior4.4', 'bior5.5', 'bior6.8'
% 'rbio1.1', 'rbio1.3', 'rbio1.5'
% 'rbio2.2', 'rbio2.4', 'rbio2.6', 'rbio2.8'
% 'rbio3.1', 'rbio3.3', 'rbio3.5', 'rbio3.7'
% 'rbio3.9', 'rbio4.4', 'rbio5.5', 'rbio6.8'
wtype = 'rbio6.8';
wlev_max = wmaxlev(N,wtype);
if wlev_max ==
    fprintf('\nThe parameter N and wtype does not match!\n');
end
dwtmode('per');
for wlev = :wlev_max
    ww = dwtmtx(N,wtype,wlev);
    x = randn(,N);
    y1 = (ww*x')';
    [y2,y2l] = wavedec(x,wlev,wtype);
    y_err = sum((y1-y2).*(y1-y2));
    fprintf('wlev = %d: y_err = %f\n',wlev,y_err);
end