[Python] Hermite 插值

　　　　　　　　

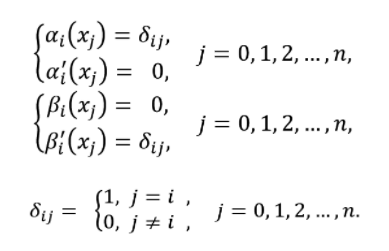
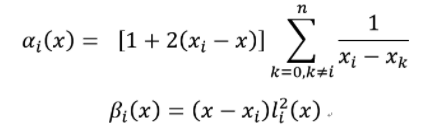
# -*- coding: utf-8 -*-
#Program 0.5 Hermite Interpolation

import matplotlib.pyplot as plt
import numpy as np

#计算基函数的导数值
def dl(i, xi):
	result = 0.0
	for j in range(0,len(xi)):
		if j!=i:
			result += 1/(xi[i]-xi[j])
	result *= 2
	return result

#计算基函数值
def l(i, xi, x):
	deno = 1.0
	nu = 1.0

	for j in range(0, len(xi)):
		if j!= i:
			deno *= (xi[i]-xi[j])
			nu *= (x-xi[j])

	return nu/deno

#Hermite插值函数
def get_Hermite(xi, yi, dyi):
	def he(x):
		result = 0.0
		for i in range(0, len(xi)):
			result += (yi[i]+(x-xi[i])*(dyi[i]-2*yi[i]*dl(i, xi))) * ((l(i,xi,x))**2)
		return result
	return he

import math
sr_x = [(i * math.pi) + (math.pi / 2) for i in range(-3, 3)]
sr_fx = [math.sin(i) for i in sr_x]
deriv = [0 for i in sr_x]                           # 导数都为 0
Hx = get_Hermite(sr_x, sr_fx, deriv)  # 获得插值函数
tmp_x = [i * 0.1 * math.pi for i in range(-20, 20)] # 测试用例
tmp_y = [Hx(i) for i in tmp_x]                      # 根据插值函数获得测试用例的纵坐标

#画图
plt.plot(sr_x, sr_fx, 'ro')
plt.plot(tmp_x, tmp_y, 'b-')
plt.title('Hermite Interpolation')
plt.show()