Deep Learning.ai学习笔记_第一门课_神经网络和深度学习

目录

前言

第一周（深度学习引言）

第二周（神经网络的编程基础）

第三周（浅层神经网络）

第四周（深层神经网络）

---

前言

目标： 掌握神经网络的基本概念， 学习如何建立神经网络（包含一个深度神经网络），以及如何在数据上面训练他们，最后将用一个深度神经网络进行辨认猫。

（1）了解深度学习的概念

（2）了解神经网络的结构，使用算法并高效地实现

（3）结合神经网络的算法实现框架，编写实现一个隐藏层神经网络

（4）建立一个深层的神经网络（一般把层数大于等于3的神经网络称为深层神经网络）

第一周（深度学习引言）

Deep Learning:

改变（应用）：网络搜索和广告推荐

很好的示例：读取X光图像、精准化农业、自动驾驶等

突破：计算机视觉（图像识别），语音识别（机器翻译）

观点： 认为AI是最新的电力，大约在一百年前，我们社会的电气化改变了每个主要行业，从交通运输行业到制造业、医疗保健、通讯等方面，我认为如今我们见到了AI明显的令人惊讶的能量，带来了同样巨大的转变。

什么是神经网络？

我的初步理解：给定原始输入数据，按照特定的计算规则传递给神经元，后续经过相应的计算规则继续传递给下一层神经元，当到达最后一层时，得到的神经元中存储的数据即为需要输出的数据。

简单描述: 尝试输入一个x，即可把它映射成y。

例如，课程中给的关于预测房屋价格的神经网络示例，如下图:

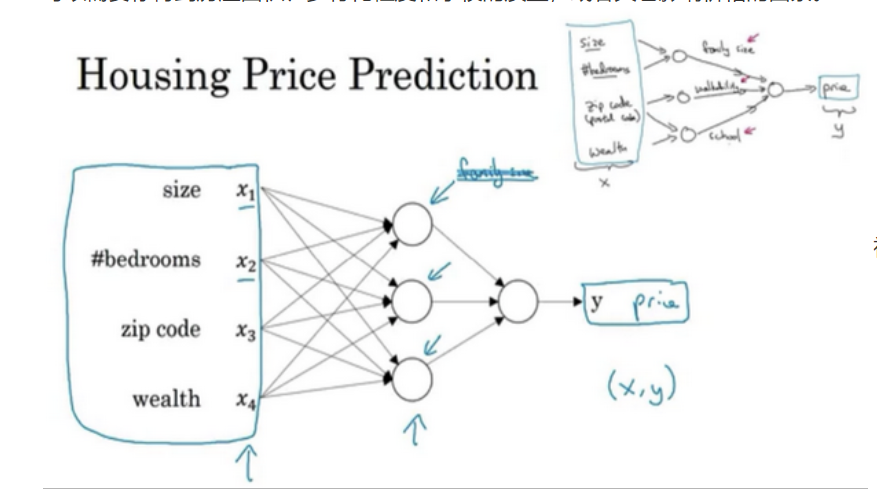
区分结构化数据和非结构化数据：

结构化数据： 数据的基本数据库， 例如在房价预测中，你可能有一个数据库，有专门的几列数据告诉你卧室的大小和数量，这就是结构化数据。

非结构化数据： 如音频，原始音频或者你想要识别的图像或文本中的内容。

什么是监督学习？

我的理解：给定大量得输入数据，以及对应得输出结果标记数据。来训练神经网络得到中间计算出对应输出结果的模型函数。成功得到该模型后，后续就可以使用该模型来预测新的输入数据的预测结果，从而得到实际价值。

简单描述：监督式学习的目标是在给定一个 (x, g（x）)的集合下，去找一个函数g。

深度学习兴起条件：

• 可以获得更多的数据
• 硬件性能的提高，比如GPU
• 计算能力大大提高
• 激活函数的选择(从sigmoid函数转换到一个ReLU函数，是神经网络应用方面的一个巨大突破。因为在进行梯度下降计算时， sigmoid函数的梯度会接近零，所以学习的速度会变得非常缓慢，因为当你实现梯度下降以及梯度接近零的时候，参数会更新的很慢，所以学习的速率也会变的很慢。然而，使用ReLU函数恰恰解决这一问题)

第二周（神经网络的编程基础）

对于本周学习的内容，需要着重理解一下几个概念及背后的实现原理：

• 梯度下降
• 逻辑回归

梯度下降：

在逻辑回归算法第三步中需要使用梯度下降法，来求取代价函数J(w, b)的最小值。

梯度下降一个简单暴力的理解：在一个函数图像中沿着函数值不断减小的梯度方向下降（向下走）叫梯度下降。此处可见参考资料[1]

现在问题是要求取J（w, b）的最小值，可以看下面一个形象化的图像：

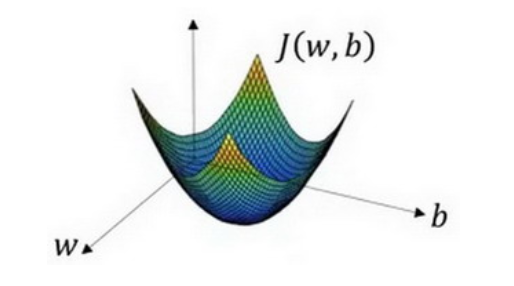
在这个图中，横轴表示你的空间参数w和b。要求J(w, b)最小值，即要求取图中曲面最低部的一点处的值即为最佳值。可以看出大小是按照梯度不断下降的方式变化。

对参数w的梯度下降更新公式（其中a是学习率，用来控制步长。:=表示更新参数）：

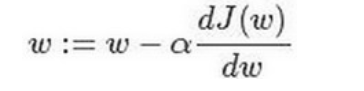
对参数b的梯度下降更新公式：

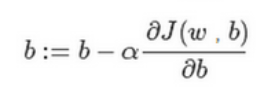
逻辑回归算法：

该算法分为三部分，分别是预测函数部分、损失函数、梯度下降法求取代价函数的最小值。此处可见参考资料[2]

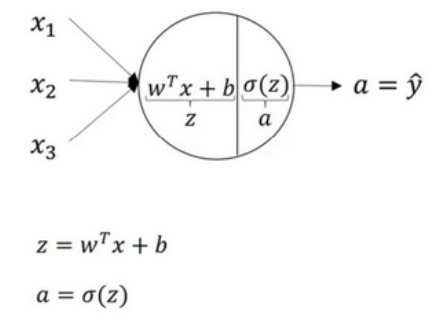
首先说一下预测函数：

给定输入数据x，传递过程中的特征权重w和偏差b，计算最终的输出预测值y，这就是预测函数需要做的事情。

一般情况下，z = wx + b，你会发现函数z是一个线性函数，而且z值得大小依据x的取值大小而不断变化，不能给神经网络的最终预测结构提供帮助。

例如，识别一张猫的图片，最终的预测结果只有两种：不是，是。因此，我们可以类似处理，把最终输出的预测值y变为0和1两种，0表示是，1表示不是。

那么如何让z转化为最终的预测值y呢？

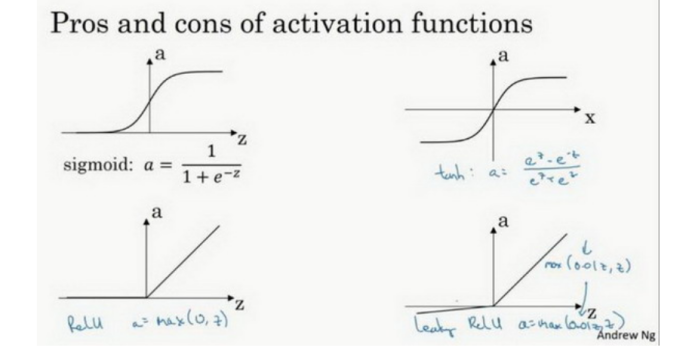
此处可以选择采用具有二分特性的sigmoid函数，sigmoid函数图像如下：

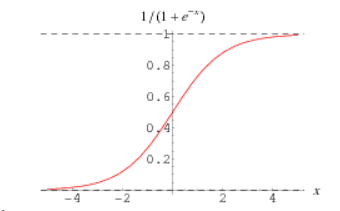
可以看出sigmoid函数的取值区间为（0，1），当x趋近正无穷大时，值趋近1，当x趋近负无穷大时，值趋近0。

那么我们可以把z值当作参数传递给sigmoid函数，如果sigmoid(z) >= 0.5就令y = 1， 否则令y = 0。

但是，逻辑回归做的处理是给出最终的估计值sigmoid(z)，具体y的值大小是神经网络最后一步的最终输出结果。（PS：注意预处理函数此处给出的示例是sigmoid函数，对应其他情况需要选择其他合适的预处理函数）一般把y^ = o(z)（PS：这里是使用有y^表示数学字符y帽，o表示预处理函数）

总结，预测函数计算步骤：

z = wx + b, y^ = o(z)，其中o是预处理函数。

损失函数：

损失函数又叫做误差函数，用来衡量算法的运行情况，Loss function:L(y^, y).

我们通过这个L称为的损失函数，来衡量预测输出值和实际值有多接近。一般我们用预测值和实际值的平方差或者它们平方差的一半，但是通常在逻辑回归中我们不这么做，因为当我们在学习逻辑回归参数的时候，会发现我们的优化目标不是凸优化，只能找到多个局部最优值，梯度下降法很可能找不到全局最优值，虽然平方差是一个不错的损失函数，但是我们在逻辑回归模型中会定义另外一个损失函数。

我们在逻辑回归中用到的损失函数是：

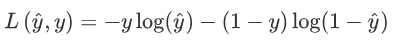
代价函数：

为了衡量算法在全部训练样本上的表现如何，我们需要定义一个算法的代价函数，算法的代价函数是对m个样本的损失函数求和然后除以m:

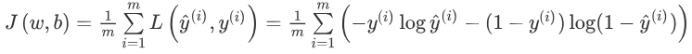
损失函数只适用于像这样的单个训练样本，而代价函数是参数的总代价，所以在训练逻辑回归模型时候，我们需要找到合适的w和b，来让代价函数J  的总代价降到最低。

最后，看几处课程中比较重要的几张图：

单个样本逻辑回归梯度下降计算过程：

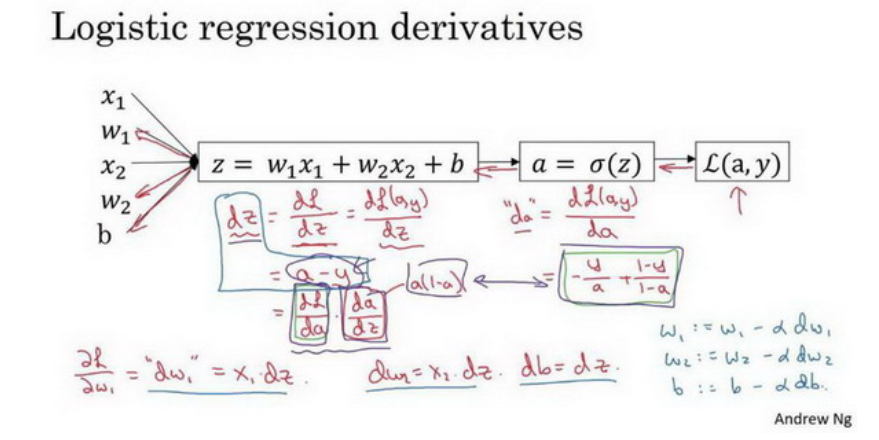
多个样本逻辑回归梯度下降计算过程：

第三周（浅层神经网络）

基于逻辑回归重复使用了两次及以上该模型就可得到神经网络，例如下图：

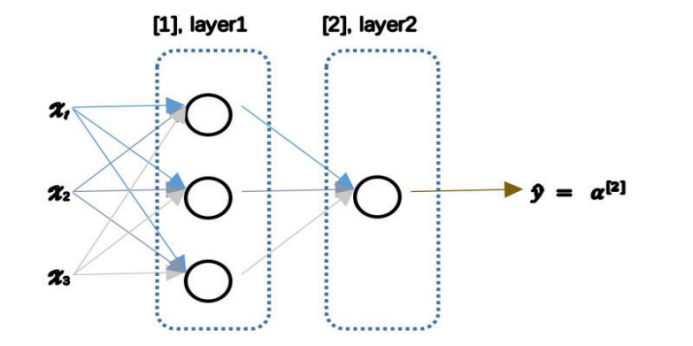
用圆圈表示神经网络的计算单元，逻辑回归的计算有两个步骤，具体如下图：

常见的激活函数：

为什么需要非线性激活函数？

如果你使用线性激活函数或者没有使用一个激活函数，那么无论你的神经网络有多少层一直在做的只是计算线性函数，所以不如直接去掉全部隐藏层。（PS： 如果你是用线性激活函数或者叫恒等激励函数，那么神经网络只是把输入线性组合再输出。）

总而言之，不能在隐藏层用线性激活函数。 唯一可以用线性激活函数的通常就是输出层；除了这种情况，会在隐层用线性函数的，除了一些特殊情况，比如与压缩有关的，那方面在这里将不深入讨论。在这之外，在隐层使用线性激活函数非常少见。

当你训练神经网络时，权重随机初始化是很重要的。对于逻辑回归，把权重初始化为0当然也是可以的。但是对于一个神经网络，如果你把权重或者参数都初始化为0，那么梯度下降将不会起作用。

如果你要初始化成0，由于所有的隐含单元都是对称的，无论你运行梯度下降多久，他们一直计算同样的函数。这没有任何帮助，因为你想要两个不同的隐含单元计算不同的函数，这个问题的解决方法就是随机初始化参数。

第四周（深层神经网络）

有一个隐藏层的神经网络，就是一个两层神经网络。记住当我们算神经网络的层数时，我们不算输入层，我们只算隐藏层和输出层。

在做深度神经网络的反向传播时，一定要确认所有的矩阵维数是前后一致的，可以大大提高代码通过率。

为什么使用深层表示？

深度神经网络的这许多隐藏层中，较早的前几层能学习一些低层次的简单特征，等到后几层，就能把简单的特征结合起来，去探测更加复杂的东西。比如你录在音频里的单词、词组或是句子，然后就能运行语音识别了。同时我们所计算的之前的几层，也就是相对简单的输入函数，比如图像单元的边缘什么的。到网络中的深层时，你实际上就能做很多复杂的事，比如探测面部或是探测单词、短语或是句子。

想要你的深度神经网络起很好的效果，你还需要规划好你的参数以及超参数。

什么是超参数？

比如算法中的learning rate a（学习率）、iterations(梯度下降法循环的数量)、L（隐藏层数目）、n[l]（隐藏层单元数目）、choice of activation function（激活函数的选择）都需要你来设置，这些数字实际上控制了最后的参数W和b的值，所以它们被称作超参数。

参考资料：

[1]https://blog.csdn.net/songhaoaa/article/details/48085083

[2] https://blog.csdn.net/ligang_csdn/article/details/53838743