最短路径之Bellman-Ford——解决负权边

Bellman-Ford算法非常简单，核心代码四行，可以完美的解决带有负权边的图。

for(k=1;k<=n-1;k++)  //外循环循环n-1次，n为顶点个数
    for(i=1;i<=m;i++)//内循环循环m次，m为边的个数，即枚举每一条边
        if(dis[v[i]]>dis[u[i]]+w[i])//尝试对每一条边进行松弛，与Dijkstra算法相同
            dis[v[i]]=dis[u[i]]+w[i]; 

上面的代码中，外循环一共循环了n-1次(n为顶点的个数)，内循环循环了m次(m为边的个数)，即枚举每一条边。dis 数组的作用与Dijkstra算法一样，是用来记录源点到其余各个顶点的最短路径。u、v和w三个数组是用来记录边的信息。例如第i条边存储在u[i]、v[i]和w[i]中，表示从顶点u[i]到顶点v[j]这条边(u[i]→v[i]) 权值为w[i]。

if(dis[v[i]]>dis[u[i]]+w[i])//尝试对每一条边进行松弛，与Dijkstra算法相同
      dis[v[i]]=dis[u[i]]+w[i];

上面这两行代码的意思是:看看能否通过u[i]→v[i] (权值为w[i])这条边，使得1号顶点到v[i]号顶点的距离变短。即1号顶点到u[i]号顶点的距离(dis[u[i]) 加上u[i]→v[i]这条边(权值为w[i])的值是否会比原先1号顶点到v[i]号顶点的距离(dis[v[]) 要小。这一点其实与Djkstra的“松弛”操作是一样的。现在我们要把所有的边都松弛一遍，代码如下。

for(i=1;i<=m;i++)//内循环循环m次，m为边的个数，即枚举每一条边
        if(dis[v[i]]>dis[u[i]]+w[i])//尝试对每一条边进行松弛，与Dijkstra算法相同
            dis[v[i]]=dis[u[i]]+w[i]; 

那把每一条边都“松弛”一遍后，究竟会有什么效果呢?现在来举个具体的例子。求下图1号顶点到其余所有顶点的最短路径。

我们还是用一一个dis数组来存储1号顶点到所有顶点的距离。

上方右图中每个顶点旁的值(带下划线的数字)为该顶点的最短路“估计值”(当前1号顶点到该顶点的距离)，即数组dis中对应的值。根据边给出的顺序，先来处理第1条边 “232”(2 →3,通过这条边进行松弛)，即判断dis[3]是否大于dis[2]+2此时dis[3]是∞, dis[2]是∞，因此dis[2]+2也是∞，所以通过“232”这条边不能使dis[3]的值变小，松弛失败。

同理，继续处理第2条边“1 2 -3”(1->2)，我们发现dis[2]大于dis[1]+(-3)， 通过这条
边可以使dis[2]的值 从∞变为-3，因此松弛成功。用同样的方法处理剩F的每一条边。 对所有的边松弛一遍后的结果如下。

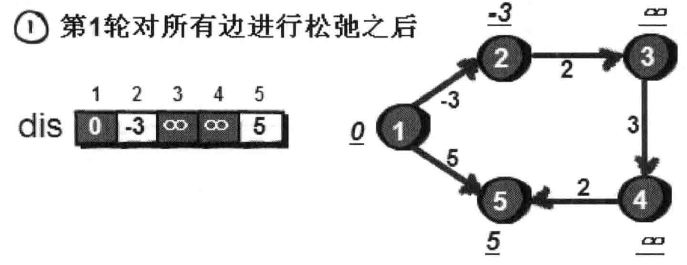
我们发现，在对每条边都进行一次松弛后，已经使得dis[2]和dis[5]的值变小，即1号顶到2号顶点的距离和1号顶点到5号顶点的距离都变短了。

接下来我们需要对所有的边再进行一轮松弛，操作过程与上一轮一样，再来看看又会发生什么变化。

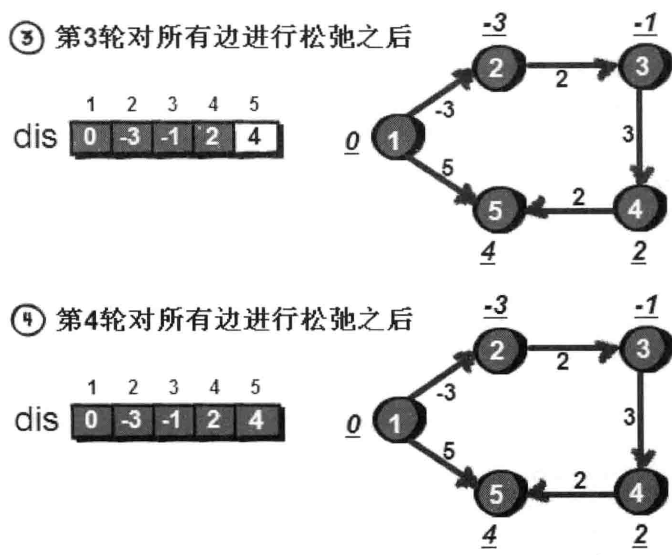
在这一轮松弛时，我们发现，现在通过“2 3 2”(2->3)这条边，可以使1号顶点到3号顶点的距离(dis[3]) 变短了。爱思考的同学就会问了，这条边在上一轮也松弛过啊，为什么上一轮松弛失败了，这一轮却成功了呢?因为在第一轮松弛过后，1号顶点到2号顶点的距离(dis[2]) 已经发生了变化，这一轮再通过“232”(2->3)这条边进行松弛的时候,已经可以使1号顶点到3号顶点的距离(dis[3]) 的值变小。

换句话说，第1轮在对所有的边进行松驰之后，得到的是从1号顶点“只能经过一条边”到达其余各顶点的最短路径长度。第2轮在对所有的边进行松弛之后，得到的是从1号顶点“最多经过两条边”到达其余各顶点的最短路径长度。如果进行k轮的话，得到的就是1号顶点“最多经过k条边”到达其余各顶点的最短路径长度。现在又有一个新问题:需要进行多少轮呢?

只需要进行n- 1轮就可以了。因为在一个含有n个顶点的图中，任意两点之间的最短路径最多包含n-1边。

有些特别爱思考的同学又会发出一个疑问:真的最多只能包含n-1条边?最短路径中不可能包含回路吗?

在一个含有n个顶点的图中，任意两点之间的最短路径最多包含n-1条边，最短路径中不可能包含回路。

因为最短路径是一个不包含回路的简单路径，回路分为正权回路(回路权值之和为正)和负权回路(回路权值之和为负)。如果最短路径中包含正权回路，那么去掉这个回路，一定可以得到更短的路径；如果最短路径中包含负权回路，那么肯定没有最短路径，因为每多走一次负权回路就可以得到更短的路径. 因此最短路径肯定是一个不包含回路的最短路径，即最多包含n-1条边

Bellman-Ford算法的主要思想：

　　首先dis数组初始化顶点u到其余各个顶点的距离为∞，dis[u] = 0。

　　然后每轮对输入的所有边进行松弛，更新dis数组，至多需要进行n-1次就可以求出顶点u到其余各顶点的最短路径（因为任意两点之间的最短路径最多包含n-1条边，所以只需要n-1轮就行）。

一句话概括Bellman-Ford算法就是：对所有边进行n-1次“松弛”操作。

此外，Bellman-Ford算法可以检测一个图是否有负权回路。如果已经进行了n-1轮松弛之后，仍然存在

if(dis[v[i]]>dis[u[i]]+w[i])
    dis[v[i]]=dis[u[i]]+w[i];

的情况，也就是说在进行n-1轮之后，仍然可以继续成功松弛，那么这个图一定存在负权回路。

关键代码如下：

//Bellman-Ford算法核心语句
for(k=1;k<=n-1;k++)  //外循环循环n-1次，n为顶点个数
    for(i=1;i<=m;i++)//内循环循环m次，m为边的个数，即枚举每一条边
        if(dis[v[i]]>dis[u[i]]+w[i])//尝试对每一条边进行松弛，与Dijkstra算法相同
            dis[v[i]]=dis[u[i]]+w[i];
//检测负权回路
flag=0;
for(i=1;i<=m;i++)
    if(dis[v[i]]>dis[u[i]]+w[i])
        flag=1;
if(flag==1)
    printf("此图有负权回路");

显然，算法复杂度为O（NM），比Dijkstra算法还高，当然可以进行优化。

在实际操作中，Bellman-Ford算法经常会在没有达到n-1轮松弛前就已经计算出最短路，上面已经说过，n-1其实是最大轮回次数。

因此可以添加一个变量check用来标记数组dis在本轮松弛中是否发生了变化，若没有变化，则提前跳出循环。

完整代码如下：

#include <stdio.h>

#define INF 999999
int main()
{
    int i, j, n, m;
    int dis[10], bak[10], u[10], v[10], w[10];
    int check, flag = 0;
    //读入n和m，n表示顶点个数，m表示边的条数
    scanf("%d %d", &n, &m);
    //读入边
    for (i = 1; i <= m; ++i)
    {
        scanf("%d %d %d", &u[i], &v[i], &w[i]);
    }
    //初始化dis数组，这里是1号顶点到其余顶点的初始路程
    for (i = 1; i <= n; ++i)
    {
        dis[i] = INF;
    }
    dis[1] = 0;

    // Bellman-Ford算法核心代码
    for (j = 1; j <= n-1; ++j)     //最多循环n-1轮
    {
        check = 0;//用来标记在本轮松弛中数组dis是否发生更新
        for (i = 1; i <= m; ++i)        // 最核心的3句Bellman-Ford算法
        {
            if (dis[v[i]] > dis[u[i]] + w[i])
            {
                dis[v[i]] = dis[u[i]] + w[i];
                check = 1;//数组dis发生更新，改变check的值
            }
        }
        //松弛完毕后检测数组dis是否有更新
        if (check==0)
        {
            break; //没有更新则提前退出程序
        }
    }

    //检测负权回路
    for (i = 1; i <= m; ++i)     // n-1次之后最短路径还会发生变化则含有负权回路
    {
        if (dis[v[i]] > dis[u[i]] + w[i])
        {
            flag = 1;
        }
    }

    if (flag==1)
    {
        printf("该图有负权回路");
    }
    else
    {
        //输出最终结果
        printf("最终结果为：\n");
        for (i = 1; i <= n; ++i)
        {
            printf(" 1号顶点到%d号顶点的最短距离为：%d\n", i,dis[i]);
        }
    }
    printf("\n");
    getchar();
    getchar();
    return 0;
}
/*
5 5
2 3 2
1 2 -3
1 5 5
4 5 2
3 4 3
最终结果为：
 1号顶点到1号顶点的最短距离为：0
 1号顶点到2号顶点的最短距离为：-3
 1号顶点到3号顶点的最短距离为：-1
 1号顶点到4号顶点的最短距离为：2
 1号顶点到5号顶点的最短距离为：4
 */

　使用Vector存边的版本。

#include <cstring>
#include <iostream>
#include <algorithm>
#define INF 0x3f3f3f3f
using namespace std;

const int N = 510, M = 10010;

int n, m;
int dist[N];

struct Edge
{
    int a, b, w;
}edges[M];

void bellman_ford()
{
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;

    for (int i = 0; i < n; i ++ )
    {
        for (int j = 0; j < m; j ++ )
        {
            int a = edges[j].a, b = edges[j].b, w = edges[j].w;
            if (dist[a] != INF && dist[b] > dist[a] + w)
                dist[b] = dist[a] + w;
        }
    }
}

int main()
{
    scanf("%d%d", &n, &m);
    for (int i = 0; i < m; i ++ )
    {
        int a, b, w;
        scanf("%d%d%d", &a, &b, &w);
        edges[i] = {a, b, w};
    }

    bellman_ford();
    for (int i = 1; i <= n; ++i) {
        cout<<dist[i]<<" ";
    }
    return 0;
}