在平衡树的海洋中畅游（三）——Splay

Preface

由于我怕学习了Splay之后不直接写blog第二天就忘了，所以强行加了一波优先级。

论谁是天下最秀平衡树，我Splay第一个不服。维护平衡只靠旋转。

一言不合转死你

由于平衡树我也介绍了两种Treap&&Scapegoat Tree，所以一些互通的东西也不讲了。

这次的亮点主要是为了弥补Splay的巨大常数（据说是96），我把大量的函数都写成了迭代版本。

废话不多说开讲。

---

维护平衡的方式——旋转

关于旋转操作，在Treap的那篇文章中已经讲的比较详细了。

但是注意一下Splay的旋转不同于Treap，一般Splay旋转时简单的理解就是儿子翻身当爸爸

什么意思，其实像这样：

\(x,y\)的关系还是很好理解的，主要是\(x\)的某个儿子被旋到哪里去了旋的头晕

我们再手玩几种情况：

• \(y\)是\(z\)的左儿子 \(x\)是\(y\)的左儿子

• \(y\)是\(z\)的左儿子 \(x\)是\(y\)的右儿子

• \(y\)是\(z\)的右儿子 \(x\)是\(y\)的右儿子

疯狂手玩ing

那我们来总结一波性质吧：

1. 我们把\(x\)转到了原来\(y\)的位置（这个很简单，因为我们旋转的本意就是让\(x\)儿子变爸爸）
2. \(x\)是\(y\)的哪个儿子，那么旋转完之后，\(x\)的那个儿子就不会变（多玩几次就好了，证明也比较简单）
3. 如果原来\(x\)是\(y\)的哪一个儿子，那么旋转完之后\(y\)就是\(x\)的另外一个儿子

然后我们就可以搞出旋转的核心代码了（具体看下面）

---

一波操作上天——伸展

为什么Splay要叫Splay呢。请自行使用词典查询Splay的意思。好了我懂了

一个节点已经不满足屈膝于它人的儿子了，我就是想俯视众生

正常的说，就是想要当根节点。真有梦想

那么让你飞，但是我只需要无脑暴力上旋就可以维护平衡这一重要性质了吗？

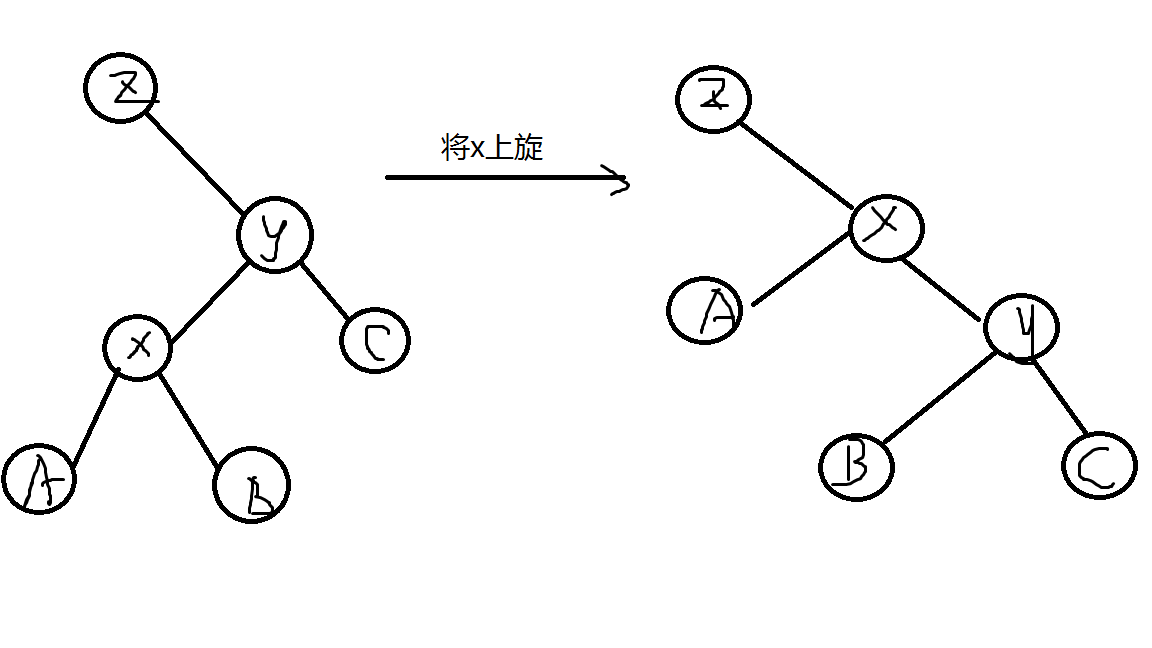
我将一个\(x\)进行上旋操作，像这样：

不是说好了要当根的吗，那我把\(x\)再旋转一波：

然后我们很意外的发现，红色的那一条链一点都没有改变

也就意味这数据还是可以把你给卡掉

然后我们发现，对于\(x,y,z\)的不同位置情况，我们要分别进行讨论

然后蒟蒻就开始\(2^3=8\)种情况大力讨论

手玩了好久好久。。。。。。

其实简化了之后也就两种：

1. \(x\)和\(y\)分别是\(y\)和\(z\)的同一个儿子
2. \(x\)和\(y\)分别是\(y\)和\(z\)的不同儿子

而对于情况一，也就是类似上面给出的图的情况，就要考虑先旋转\(y\)再旋转\(x\)

而对于情况二，自己画一下图，发现就是对\(x\)旋转两次，先旋转到\(y\)再旋转到\(x\)

于是我们就可以简化一波操作，就完成了Splay的核心内容。

---

其它操作及模板

其它的一些操作都是具有BST性质的了，就是主要一点：

有事没事Splay一下要不然干嘛叫Splay

还是板子题：Luogu P3369 【模板】普通平衡树的CODE（跑的并不慢）

#include<cstdio>
#include<cctype>
#define lc(x) (node[x].ch[0])
#define rc(x) (node[x].ch[1])
#define fa(x) (node[x].fa)
#define tc() (A==B&&(B=(A=fl)+fread(fl,1,S,stdin),A==B)?EOF:*A++)
#define pc(ch) (top<S?st[top++]=ch:(fwrite(st,1,S,stdout),st[(top=0)++]=ch))
using namespace std;
const int N=100005,S=1<<20,INF=2147483647;
char fl[S],st[S],*A=fl,*B=fl;
struct Splay
{
    int ch[2],size,cnt,fa,val;
}node[N];//同Treap，注意记录节点重复个数
int n,opt,x,rt,tot,top;
inline void read(int &x)
{
    x=0; char ch; int flag=1; while (!isdigit(ch=tc())) flag=ch^'-'?1:-1;
    while (x=(x<<3)+(x<<1)+ch-'0',isdigit(ch=tc())); x*=flag;
}
inline void write(int x)
{
    if (x<0) pc('-'),x=-x;
    if (x>9) write(x/10); pc(x%10+'0');
}
inline void pushup(int now)//更新操作，和一般的BST大同小异
{
    node[now].size=node[lc(now)].size+node[rc(now)].size+node[now].cnt;
}
inline int build(int val,int fa)//新建一个节点
{
    node[++tot].val=val; node[tot].size=node[tot].cnt=1; fa(tot)=fa;
    lc(tot)=rc(tot)=0; if (fa) node[fa].ch[val>node[fa].val]=tot; return tot;
}
inline int identify(int now)//确认一个点是它父亲的左儿子(0)还是右儿子(1)
{
    return node[fa(now)].ch[1]==now;
}
inline void connect(int son,int fa,int d)//链接两个节点，d(0/1)表示方向
{
    fa(son)=fa; node[fa].ch[d]=son;
}
inline void rotate(int now)//核心操作，上旋。注意connect的次序，最容易写错的就是pushup，不能pushup反了
{
    int x=node[now].fa,y=node[x].fa,dx=identify(now),dy=identify(x),son=node[now].ch[dx^1];
    connect(son,x,dx); connect(x,now,dx^1); connect(now,y,dy); pushup(x); pushup(now);
}
inline void splay(int now,int tar)//splay，将now伸展成为tar的儿子,注意讨论父节点即为根的情况
{
    while (fa(now)!=tar)
    {
        if (fa(fa(now))!=tar)
        {
            if (identify(now)^identify(fa(now))) rotate(now); else rotate(fa(now));
        } rotate(now);
    }
    if (!tar) rt=now;
}
inline void get_rank(int val)//查询一个点的排名，并把它旋转到根
{
    int now=rt; if (!now) return;
    while (node[now].val!=val&&node[now].ch[val>node[now].val])
    now=node[now].ch[val>node[now].val]; splay(now,0);
}
inline int get_val(int rk)//得到排名为rk的值
{
    int now=rt;
    for (;;)
    {
        if (rk>node[lc(now)].size+node[now].cnt) rk-=node[lc(now)].size+node[now].cnt,now=rc(now);
        else if (node[lc(now)].size>=rk) now=lc(now); else return node[now].val;
    }
}
inline int next(int val,int d)//精简的求前驱(0)，后继(1)的过程，注意特判
{
    get_rank(val); int now=rt;
    if ((node[now].val>val&&d)||(node[now].val<val&&!d)) return now;
    now=node[now].ch[d]; while (node[now].ch[d^1]) now=node[now].ch[d^1]; return now;
}
inline void insert(int val)//插入一个新的节点，由于此时平衡性得不到保证所以又要splay到根
{
    int now=rt,fa=0;
    while (now&&node[now].val!=val) fa=now,now=node[now].ch[val>node[now].val];
    if (!now) now=build(val,fa); else ++node[now].cnt; splay(now,0);
}
inline void remove(int val)//删除就是把一个点的前驱后继都旋上去，此时这个点就成为叶子节点了，再进行删除
{
    int lst=next(val,0),nxt=next(val,1); splay(lst,0); splay(nxt,lst); int del=lc(nxt);
    if (node[del].cnt>1) --node[del].cnt,splay(del,0); else lc(nxt)=0;
}
int main()
{
    //freopen("CODE.in","r",stdin); freopen("CODE.out","w",stdout);
    register int i; read(n); insert(-INF); insert(+INF);
    for (i=1;i<=n;++i)
    {
        read(opt); read(x);
        switch (opt)
        {
            case 1:insert(x);break;
            case 2:remove(x);break;
            case 3:get_rank(x),write(node[lc(rt)].size),pc('\n');break;
            case 4:write(get_val(x+1)),pc('\n');break;
            case 5:write(node[next(x,0)].val),pc('\n');break;
            case 6:write(node[next(x,1)].val),pc('\n');break;
        }
    }
    return fwrite(st,1,top,stdout),0;
}

平衡树的精髓在于它们不同的维护平衡的方式：

• Treap的代码精简且常数较小，是解决大部分平衡树问题的最好工具
• Scapegoat Tree的思想易于理解，且一般情况下速率良好。其内核的思想也应用到了许多其他的地方
• Splay由于它特殊的旋转性质，使其可以像线段树一样维护区间，也是LCT的辅助树，功能强大。常数也很大