【转载】LCT

原标题：LCT（Link-Cut Tree）详解（蒟蒻自留地）

出处：https://blog.csdn.net/saramanda/article/details/55253627

如果你还没有接触过LCT，你可以先看一看这里：

（看不懂没关系，先留个大概的印像）http://www.cnblogs.com/BLADEVIL/p/3510997.html

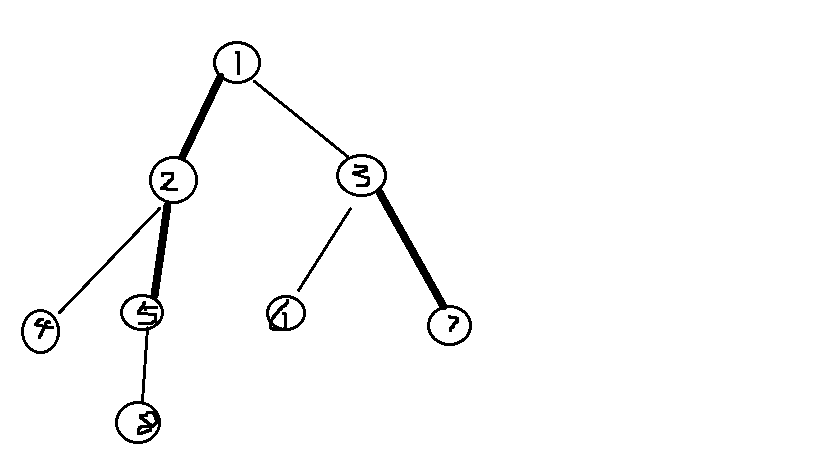
看完之后我们知道，LCT和静态的树链剖分很像。怎么说呢？这两种树形结构都是由若干条长度不等的“重链”和“轻边”构成（名字可以不同，大概就是这个意思），“重链”之间由”轻边”连接。就像这样：

可以想象为一棵树被人为的砍成了一段段。

LCT和树链剖分不同的是，树链剖分的链是不会变化的，所以可以很方便的用线段树维护。但是，既然是动态树，那么树的结构形态将会发生改变，所以我们要用更加灵活的维护区间的结构来对链进行维护，不难想到Splay可以胜任。如何分离树链也是保证时间效率的关键（链的数量和长度要平衡），树链剖分的“重儿子”就体现了前人博大精深的智慧。

在这里解释一下为什么要把树砍成一条条的链：我们可以在logn的时间内维护长度为n的区间（链），所以这样可以极大的提高树上操作的时间效率。在树链剖分中，我们把一条条链放到线段树上维护。但是LCT中，由于树的形态变化，所以用能够支持合并、分离、翻转等操作的Splay维护LCT的重链（注意，单独一个节点也算是一条重链）。

这时我们注意到，LCT中的轻边信息变得无法维护。为什么呢？因为Splay只维护了重链，没有维护重链之间的轻边；而LCT中甚至连根都可以不停的变化，所以也没法用点权表示它父边的边权（父亲在变化）。所以，如果在LCT中要维护边上信息，个人认为最方便的方法应该是把边变成一个新点和两条边。这样可以把边权的信息变成点权维护，同时为了不影响，把真正的树上节点的点权变成0，就可以用维护点的方式维护边。

LCT的各种操作：

LCT中用Splay维护链，这些Splay叫做“辅助树“。辅助树以它上面每个节点的深度为关键字维护，就是辅助树中每个节点左儿子的深度小于当前节点的深度，当前节点的深度小于右儿子的深度。

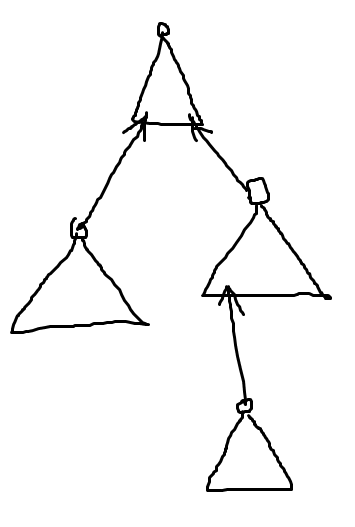
可以把LCT认为是一个由Splay组成的森林，就像这样：（三角形代表一棵Splay，对应着LCT上一条链）

箭头是什么意思呢？箭头记录着某棵Splay对应的链向上由轻边连着哪个节点，可以想象为箭头指向“Splay 的父亲”。但是，Splay的父亲并不记录有这个儿子，即箭头是单向的。同时，每个节点要记录它是否是它所在的Splay的根。这样，Splay构成的森林就建成了。

这个是我的Splay节点最基本的定义：（如果要维护更多信息就像Splay维护区间那样加上更多标记）

1.  
   struct node{
2.  
   int fa,ch[2]; //父亲和左右儿子。
3.  
   bool reverse,is_root; //区间反转标记、是否是所在Splay的根
4.  
   }T[maxn];

LCT中基本的Splay上操作：

1.  
   int getson(int x){
2.  
   return x==T[T[x].fa].ch[1];
3.  
   }
4.  
   void pushreverse(int x){
5.  
   if(!x)return;
6.  
   swap(T[x].ch[0],T[x].ch[1]);
7.  
   T[x].reverse^=1;
8.  
   }
9.  
   void pushdown(int x){
10.  
    if(T[x].reverse){
11.  
    pushreverse(T[x].ch[0]);
12.  
    pushreverse(T[x].ch[1]);
13.  
    T[x].reverse=false;
14.  
    }
15.  
    }
16.  
    void rotate(int x){
17.  
    if(T[x].is_root)return;
18.  
    int k=getson(x),fa=T[x].fa;
19.  
    int fafa=T[fa].fa;
20.  
    pushdown(fa);pushdown(x); //先要下传标记
21.  
    T[fa].ch[k]=T[x].ch[k^1];
22.  
    if(T[x].ch[k^1])T[T[x].ch[k^1]].fa=fa;
23.  
    T[x].ch[k^1]=fa;
24.  
    T[fa].fa=x;
25.  
    T[x].fa=fafa;
26.  
    if(!T[fa].is_root)T[fafa].ch[fa==T[fafa].ch[1]]=x;
27.  
    else T[x].is_root=true,T[fa].is_root=false;
28.  
    //update(fa);update(x); //如果维护了信息，就要更新节点
29.  
    }
30.  
    void push(int x){
31.  
    if(!T[x].is_root)push(T[x].fa);
32.  
    pushdown(x);
33.  
    }
34.  
    void Splay(int x){
35.  
    push(x); //在Splay到根之前，必须先传完反转标记
36.  
    for(int fa;!T[x].is_root;rotate(x)){
37.  
    if(!T[fa=T[x].fa].is_root){
38.  
    rotate((getson(x)==getson(fa))?fa:x);
39.  
    }
40.  
    }
41.  
    }

access操作：

这是LCT最核心的操作。其他所有操作都要用到它。

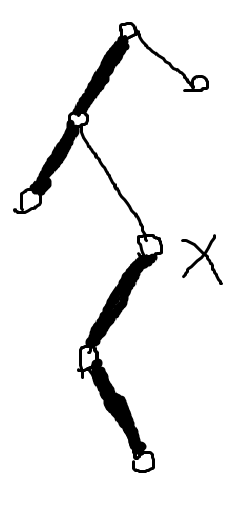
他的含义是”访问某节点“。作用是：对于访问的节点x，打通一条从树根（真实的LCT树）到x的重链；如果x往下是重链，那么把x往下的重边改成轻边。可以理解为专门开辟一条x到根的路径，由一棵Splay维护这条路径。

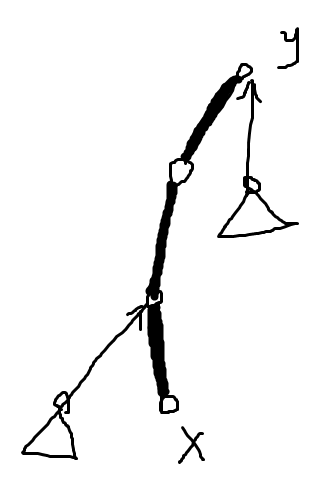
access之前：（粗的是重链）        access之后：

access实现的方式很简单；

先把x旋转到所在Splay的根，然后把x的右孩子的is_root设为true（此时右孩子对应的是x下方的重链，这样就断开了x和下方的重链）。

用y记录上一次的x（初始化y=0），把y接到x的右孩子上，这样就把上一次的重链接到了当前重链一起，同时记得T[y].is_root=false。

记录y=x，然后x=T[x].fa，把x上提。重复上面的步骤直到x=0。

代码：

1.  
   void access(int x){
2.  
   int y=0;
3.  
   do{
4.  
   Splay(x);
5.  
   T[T[x].ch[1]].is_root=true;
6.  
   T[T[x].ch[1]=y].is_root=false;
7.  
   //update(x); //如果维护了信息记得更新。
8.  
   x=T[y=x].fa;
9.  
   }while(x);
10.  
    }

mroot操作：

这个操作的作用是把某个节点变成树根（这里的根指的是整棵LCT的根）。加上access操作，就可以方便的提取出LCT上两点之间的路径。提取u到v的路径只需要mroot(u),access(v),然后v所在的Splay对应的链就是u到v的路径。

mroot实现的方式：

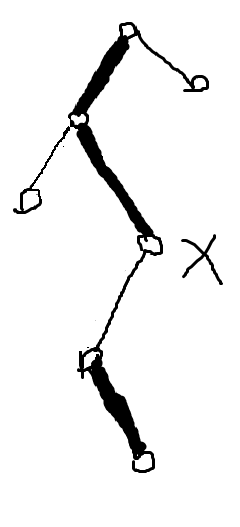
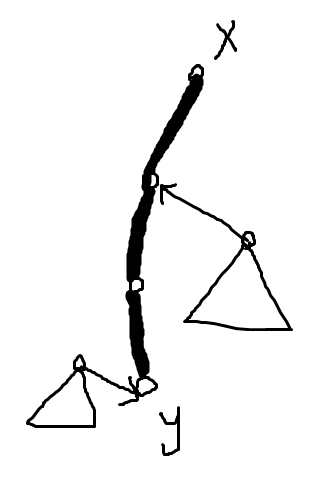
由于LCT是Splay组成的森林，所以要把x变成根就只需要让所有Splay的父亲最终指向x所在Splay。所以先access(x),Splay(x)，把现在的根和将成为根的x链在一棵Splay中，并转到根即可。但是我们注意到，由于x成为了新的根，所以它和原来的根所在的Splay中深度作为关键字的性质遭到了破坏：新根x应该是Splay中深度最小的，但是之前的操作并不会改变x的深度（也就是目前x依旧是当前Splay中深度最深的）。所以，我们需要把所在的这棵Splay翻转过来。

（粗的是重链，y是原来的根）

翻转前：                                                                      翻转后：

这时候x才真正变成了根。

代码：

1.  
   void mroot(int x){
2.  
   access(x);
3.  
   Splay(x);
4.  
   pushreverse(x);
5.  
   }

link操作：

这个操作的作用是连接两棵LCT。对于link(u,v)，表示连接u所在的LCT和v所在的LCT；

link实现的方式：

很简单，只需要先mroot(u),然后记录T[u].fa=v就可以了，就是把一个Splay森林连到另一个上。

代码：

1.  
   void link(int u,int v){
2.  
   mroot(u);
3.  
   T[u].fa=v;
4.  
   }

cut操作：

这个操作的作用是分离出两棵LCT。

代码：

1.  
   void cut(int u,int v)
2.  
   mroot(u); //先把u变成根
3.  
   access(v);Splay(v); //连接u、v
4.  
   pushdown(v); //先下传标记
5.  
   T[u].fa=T[v].ch[0]=0;
6.  
   //v的左孩子表示v上方相连的重链
7.  
   //update(v); //记得维护信息
8.  
   }

这些就是LCT的基本操作。我推荐几个LCT的练习题：

bzoj2049 SDOI2008洞穴勘探

模板题，只需要link和cut，然后询问连通性。题解：

http://blog.csdn.net/saramanda/article/details/55210235

bzoj2002 HNOI2010弹飞绵羊

模板题，需要link和询问某点到根的路径长度。题解：

http://blog.csdn.net/saramanda/article/details/55210418

bzoj3669 NOI2014魔法森林

LCT的综合应用。题解：

http://blog.csdn.net/saramanda/article/details/55250852