Necklace of Beads POJ - 1286

\(\color{#0066ff}{ 题目描述 }\)

一个圈上有n个珠子，有三种颜色可以染，问本质不同的方案数（通过旋转和翻转重合的算一种）

\(\color{#0066ff}{输入格式}\)

多组数据，每次一个n，以-1结束

\(\color{#0066ff}{输出格式}\)

每组数据输出一行一个数表示方案数

\(\color{#0066ff}{输入样例}\)

4
5
-1

\(\color{#0066ff}{输出样例}\)

21
39

\(\color{#0066ff}{数据范围与提示}\)

\(n\le 23\)

\(\color{#0066ff}{题解}\)

---------------------以下内容来自lzxkj的md。。。。qwq主要是我懒得写

我们考虑一下存在多少种置换 旋转 翻转

首先我们可以讨论\(n\)种旋转的置换

\[ans+=\sum_{i=0}^{n-1}3^{gcd(i,n)}
\]

这道题\(n≤24\) 所以可以直接写暴力的写法

接下来考虑翻转 至于翻转 我们需要讨论\(n\)的奇偶性

\(n\)为奇数时 当前的圆环可以选择穿过一个点的直线作为对称中心进行翻转

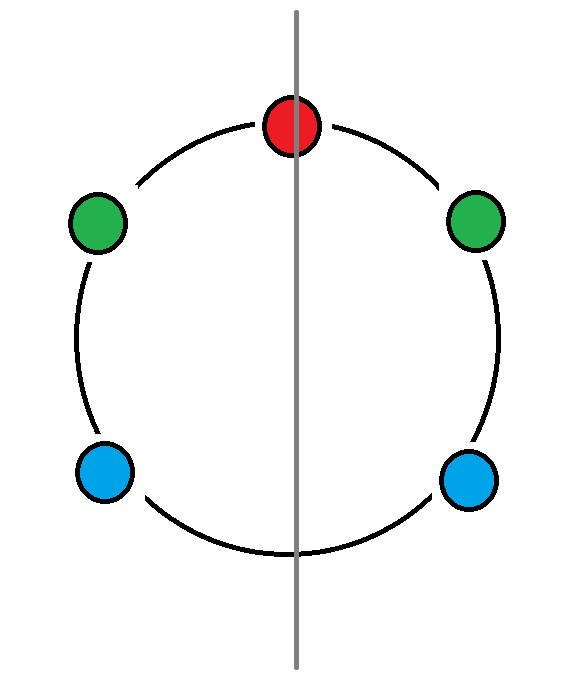
**对称的点必须相同 然后中间的那个点可以随便 **

同时每一个点作为对称点都存在相同数量的方案

所以答案是

\[3*3^{\lfloor \frac{n}{2}\rfloor}=3^{\lfloor \frac{n}{2}\rfloor +1}
\]

\(n\)为偶数时 当前的圆环可以选一条穿过两个点的直线或者一个点也没有穿过的直线作为对称轴

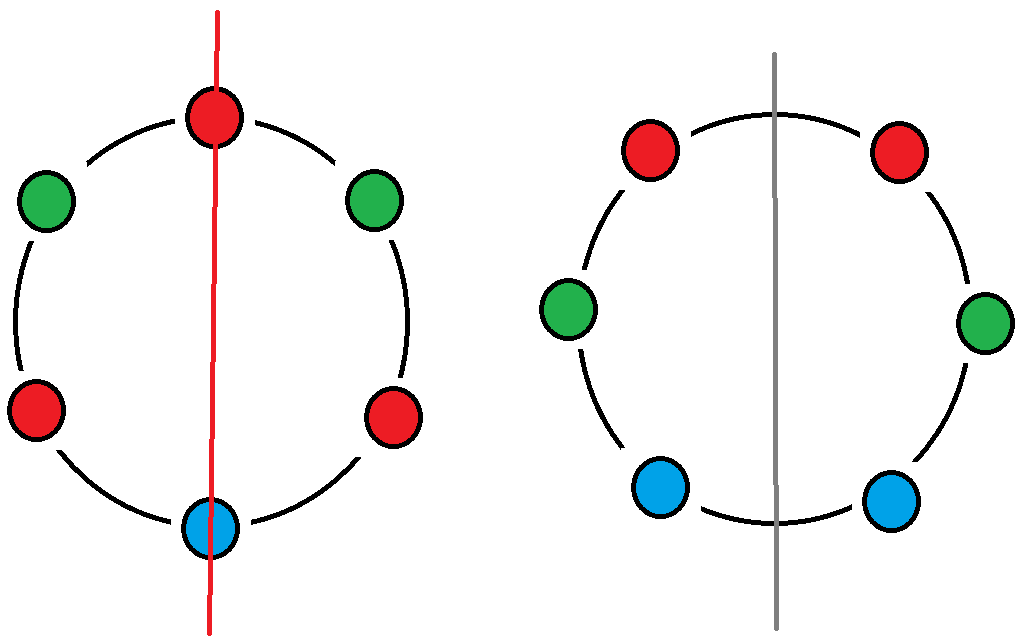
对于左图 我们可以选择\(\frac{n}{2}\)个点

**因为一个被选择的时候另一个也会被选择 ** 所以我们可以仅考虑\(\frac{n}{2}\)个点

还是**对称的点必须相同 然后中间的那两个点可以随便 **

对于右图 我们也是考虑\(\frac{n}{2}\)个空隙 理由同上

还是**对称的点必须相同 然后中间。。。。。。 **

\[\frac{n}{2}* (3*3*3^{\frac{n-2}{2}}+3^\frac{n}{2})=\frac{n}{2}*(3^\frac{n+2}{2}+3^\frac{n}{2})
\]

最后一共是有\((2*n)​\)个置换

下面是我的代码(^_)

#include<cstdio>
#include<cctype>
#define LL long long
LL in() {
	char ch; LL x = 0, f = 1;
	while(!isdigit(ch = getchar()))(ch == '-') && (f = -f);
	for(x = ch ^ 48; isdigit(ch = getchar()); x = (x << 1) + (x << 3) + (ch ^ 48));
	return x * f;
}
LL ans, n, m = 3;
LL ksm(LL x, LL y) {
	LL re = 1LL;
	while(y) {
		if(y & 1) re = re * x;
		x = x * x;
		y >>= 1;
	}
	return re;
}
LL gcd(LL x, LL y) { return y? gcd(y, x % y) : x; }
int main() {
	while(~(n = in())) {
		if(!n) {
			puts("0");
			continue;
		}
		ans = 0;
		for(int i = 0; i < n; i++) ans += ksm(m, gcd(i, n));
		if(n & 1) ans += m * n * ksm(m, (n - 1) >> 1LL);
		else ans += (n >> 1LL) * (ksm(m, n >> 1LL) + m * m * ksm(m, (n - 2) >> 1LL));
		ans /= (n << 1LL);
		printf("%lld\n", ans);
	}
	return 0;
}