erlang 最大公约数

一般面试会遇到问一些算法，什么排序，树，图等等，冷不丁还会问几个蛋疼的问题，我估计生产情况十有八九都用不上，只是题目罢了。

题目：求两个大数的最大公约数。

什么是最大公约数呢？

百度百科的答案这样的：最大公约数，指两个或多个整数共有约数中最大的一个。

大白话就是,(小学数学学过的)就是能被多个整数整除，其中最大的一个，叫做最大公约数。

辗转相除法定义

1）辗转相除法：以大数除以小数，如果能整除，那么小数就是所求的最大公约数（Greatest CommonDivisor：gcd）。否则就用余数来除刚才的除数； 再用这新除法的余数去除刚才的余数。依此类推，直到一个除法能够整除，这时作为除数的数就是        所求的最大公约数。即：gcd（x,y）表示x与y的 最大公约数，有gcd(x,y)=gcd（y,x%y），如此便可把原问题转化为求两个更小数的公约数，直到其中一个数为0，剩下的另外一个数就是两者的最大公约数。

例如：求 4453 和 5767 的最大公约数时，可作如下除法．

5767÷4453＝1 余 1314

4453÷1314＝3 余 511

      1314÷511 ＝2 余 292 

      511 ÷292 ＝1 余 219 

      292 ÷219 ＝1 余 73 

      219÷73＝3

    于是得知，5767 和 4453 的最大公约数是 73。辗转相除法适用比较广，比短除法要好得多，它能保证求出任意两个数的最大公约数。

C语言中，通过递归可简单实现，具体如下：

  int Euclidean_Recursion(int m, int n) {
      if (n == 0)
          return m;
      return method1(n, m % n);
  }

erlang的实现，具体如下：

-module(common_divisor).

-export([test/2]).

%两个数的最大公约数
test(M,N) ->
        if N == 0 -> M;
            true -> test(N, M rem N)
        end. 

打印结果：

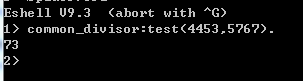
结果为73