正定矩阵(Positive-definite Matrix)
正定矩阵是自共轭矩阵的一种。正定矩阵类似复数中的正实数。定义:对于对称矩阵M,当且仅当存在任意向量x,都有
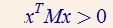
若上式大于等于零,则称M为半正定矩阵。正定矩阵记为M>0。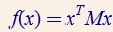
也被称为正定二次型
正定矩阵的判定
1、所有特征值为正数(根据谱定理,若条件成立,必然可以找到对角矩阵的D和正定矩阵P,使M=P^-1DP);
2、所有的顺序主子式为正定;
3、Cholesky分解得到的矩阵,其主对角线上的元素全为正数;
4、矩阵有半双线性映射形式。
首先解释双线性映射。假设三个向量空间X, Y和Z,有Z = B(X, Y)。对于X或Y中的任意向量都有到Z的唯一映射。如果把X固定,Y中的元素就存在到Z的线性映射,反过来也一样。
所谓半双线性映射,就是它的两个参数一个是线性的,另一个是半线性的(或共轭线性)。如: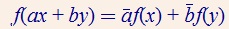
复数空间的内积都是半双线性的。
正定矩阵的性质
1、正定矩阵均可逆,且逆矩阵也为正定矩阵;
2、正定矩阵与正实数的乘积也为正定;
3、迹Tr(M)>0;
4、存在唯一的平方根矩阵B,使得: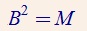
正定矩阵(Positive-definite Matrix)的更多相关文章
- 【线性代数】6-5:正定矩阵(Positive Definite Matrices)
title: [线性代数]6-5:正定矩阵(Positive Definite Matrices) categories: Mathematic Linear Algebra keywords: Po ...
- 正定矩阵(positive definite matrix)
设M是n阶方阵,如果对任何非零向量z,都有zTMz> 0,其中zT 表示z的转置,就称M正定矩阵. 正定矩阵在合同变换下可化为标准型, 即对角矩阵. 所有特征值大于零的对称矩阵也是正定矩阵. ...
- 正定矩阵(definite matrix)
1. 基本定义 在线性规划中,一个对称的 n×n 的实值矩阵 M,如果满足对于任意的非零列向量 z,都有 zTMz>0. 更一般地,对于 n×n 的 Hermitian 矩阵(原矩阵=共轭转置, ...
- a positive definite matrix
https://en.wikipedia.org/wiki/Definite_quadratic_form https://www.math.utah.edu/~zwick/Classes/Fall2 ...
- Cholesky分解 平方根法
一种矩阵运算方法,又叫Cholesky分解.所谓平方根法,就是利用对称正定矩阵的三角分解得到的求解对称正定方程组的一种有效方法.它是把一个对称正定的矩阵表示成一个下三角矩阵L和其转置的乘积的分解.它要 ...
- cholesky分解
接着LU分解继续往下,就会发展出很多相关但是并不完全一样的矩阵分解,最后对于对称正定矩阵,我们则可以给出非常有用的cholesky分解.这些分解的来源就在于矩阵本身存在的特殊的 结构.对于矩阵 ...
- 从线性模型(linear model)衍生出的机器学习分类器(classifier)
1. 线性模型简介 0x1:线性模型的现实意义 在一个理想的连续世界中,任何非线性的东西都可以被线性的东西来拟合(参考Taylor Expansion公式),所以理论上线性模型可以模拟物理世界中的绝大 ...
- AI人工智能专业词汇集
作为最早关注人工智能技术的媒体,机器之心在编译国外技术博客.论文.专家观点等内容上已经积累了超过两年多的经验.期间,从无到有,机器之心的编译团队一直在积累专业词汇.虽然有很多的文章因为专业性我们没能尽 ...
- [C9] 降维(Dimensionality Reduction)
降维(Dimensionality Reduction) 动机一:数据压缩(Motivation I : Data Compression) 数据压缩允许我们压缩数据,从而使用较少的计算机内存或磁盘空 ...
- Mahout 系列之----共轭梯度
无预处理共轭梯度 要求解线性方程组 ,稳定双共轭梯度法从初始解 开始按以下步骤迭代: 任意选择向量 使得 ,例如, 对 若 足够精确则退出 预处理共轭梯度 预处理通常被用来加速迭代方法的收敛.要使用预 ...
随机推荐
- Charles抓包使用总结
一.简介 Charles是目前最强大最流行的http抓包调试工具,Mac.Unix.Windows各个平台都支持.特别是做APP开发,调试与服务端的通信,Charles是必备工具. 二.Charles ...
- protobuf在c++的使用方法以及在linux安装
https://blog.csdn.net/wangyin668/article/details/80046798 https://www.cnblogs.com/zhouyang209117/p ...
- Transition FrameWork
Android Transition Framework可以实现三种效果: 不同Activity之间切换时,Activityc的内容(contentView)转场动画 不同Activity之间切换时, ...
- 20181031 temp
https://wiki.jenkins.io/display/JENKINS/M2+Release+Plugin https://issues.jenkins-ci.org/browse/JENKI ...
- 性能测试工具LoadRunner10-LR之Virtual User Generator 错误处理函数
VuGen提供了错误处理函数lr_continue_on_error,用来在脚本中实时修改Vuser的出错设置.lr_continue_on_error函数语法结构如下: void lr_contin ...
- 《nginx 二》深入理解nginx的各项配置
Nginx应用场景 1.http服务器.Nginx是一个http服务可以独立提供http服务.可以做网页静态服务器. 2.虚拟主机.可以实现在一台服务器虚拟出多个网站,例如个人网站使用的虚拟机. 3. ...
- HDU 5335——Walk Out——————【贪心】
Walk Out Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/65536 K (Java/Others)Total Su ...
- jq中哪个方法有回调函数
animate();id为btn的div ,位置由页面下方-100px出现,后消失 $(“#btn”).animate({ position:"absolute",bottom:& ...
- [JAVA][Liferay] Configure sharding in multiple sites
create databases first portal-ext.properties配置 hibernate.dialect=org.hibernate.dialect.PostgreSQLDia ...
- Hibernate课程 初探一对多映射5-1 课程总结
1 单方一对多 xml one-to-many 配置 实体类 一方添加保存多方集合 2 单方多对一 xml many-to-one 配置 实体类 多方添加保存一方引用 3 常用属性 inver ...
